Causal Discovery by Kernel Intrinsic Invariance Measure
Paper and Code
Sep 02, 2019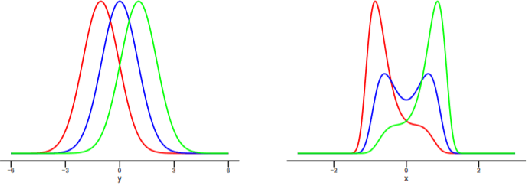
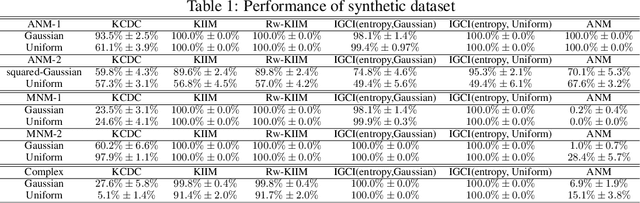
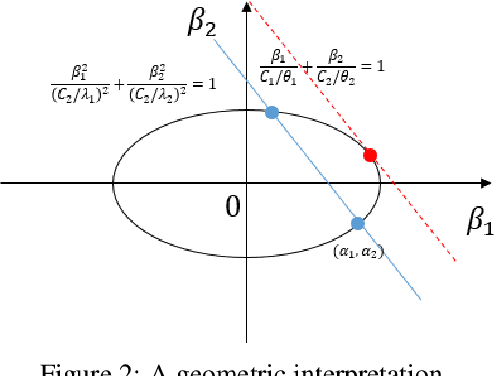
Reasoning based on causality, instead of association has been considered as a key ingredient towards real machine intelligence. However, it is a challenging task to infer causal relationship/structure among variables. In recent years, an Independent Mechanism (IM) principle was proposed, stating that the mechanism generating the cause and the one mapping the cause to the effect are independent. As the conjecture, it is argued that in the causal direction, the conditional distributions instantiated at different value of the conditioning variable have less variation than the anti-causal direction. Existing state-of-the-arts simply compare the variance of the RKHS mean embedding norms of these conditional distributions. In this paper, we prove that this norm-based approach sacrifices important information of the original conditional distributions. We propose a Kernel Intrinsic Invariance Measure (KIIM) to capture higher order statistics corresponding to the shapes of the density functions. We show our algorithm can be reduced to an eigen-decomposition task on a kernel matrix measuring intrinsic deviance/invariance. Causal directions can then be inferred by comparing the KIIM scores of two hypothetic directions. Experiments on synthetic and real data are conducted to show the advantages of our methods over existing solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge