Integrated Sensing and Communication enabled Doppler Frequency Shift Estimation and Compensation

Despite the millimeter wave technology fulfills the low-latency and high data transmission, it will cause severe Doppler Frequency Shift (DFS) for high-speed vehicular network, which tremendously damages the communication performance. In this paper, we propose an Integrated Sensing and Communication (ISAC) enabled DFS estimation and compensation algorithm. Firstly, the DFS is coarsely estimated and compensated using radar detection. Then, the designed preamble sequence is used to accurately estimate and compensate DFS. In addition, an adaptive DFS estimator is designed to reduce the computational complexity. Compared with the traditional DFS estimation algorithm, the improvement of the proposed algorithm is verified in bit error rate and mean square error performance by simulation results.

Directional FDR Control for Sub-Gaussian Sparse GLMs

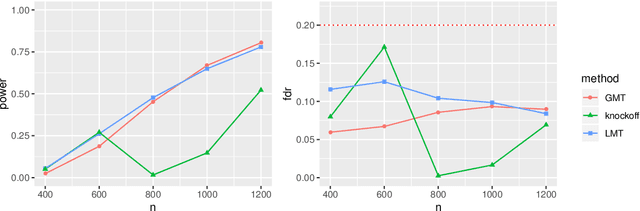
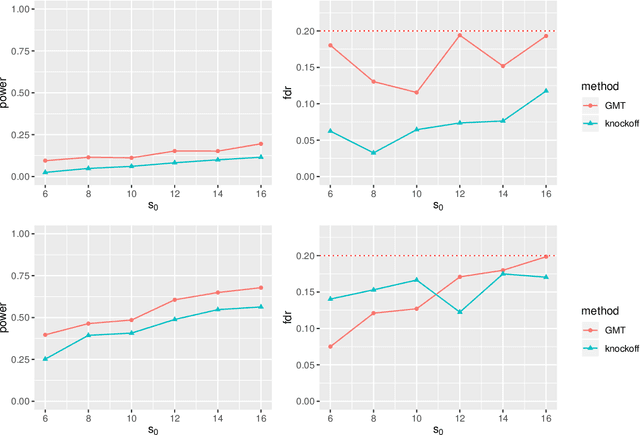
High-dimensional sparse generalized linear models (GLMs) have emerged in the setting that the number of samples and the dimension of variables are large, and even the dimension of variables grows faster than the number of samples. False discovery rate (FDR) control aims to identify some small number of statistically significantly nonzero results after getting the sparse penalized estimation of GLMs. Using the CLIME method for precision matrix estimations, we construct the debiased-Lasso estimator and prove the asymptotical normality by minimax-rate oracle inequalities for sparse GLMs. In practice, it is often needed to accurately judge each regression coefficient's positivity and negativity, which determines whether the predictor variable is positively or negatively related to the response variable conditionally on the rest variables. Using the debiased estimator, we establish multiple testing procedures. Under mild conditions, we show that the proposed debiased statistics can asymptotically control the directional (sign) FDR and directional false discovery variables at a pre-specified significance level. Moreover, it can be shown that our multiple testing procedure can approximately achieve a statistical power of 1. We also extend our methods to the two-sample problems and propose the two-sample test statistics. Under suitable conditions, we can asymptotically achieve directional FDR control and directional FDV control at the specified significance level for two-sample problems. Some numerical simulations have successfully verified the FDR control effects of our proposed testing procedures, which sometimes outperforms the classical knockoff method.

Elastic-net regularized High-dimensional Negative Binomial Regression: Consistency and Weak Signals Detection

We study sparse high-dimensional negative binomial regression problem for count data regression by showing non-asymptotic merits of the Elastic-net regularized estimator. With the KKT conditions, we derive two types of non-asymptotic oracle inequalities for the elastic net estimates of negative binomial regression by utilizing Compatibility factor and Stabil Condition, respectively. Based on oracle inequalities we proposed, we firstly show the sign consistency property of the Elastic-net estimators provided that the non-zero components in sparse true vector are large than a proper choice of the weakest signal detection threshold, and the second application is that we give an oracle inequality for bounding the grouping effect with high probability, thirdly, under some assumptions of design matrix, we can recover the true variable set with high probability if the weakest signal detection threshold is large than 3 times the value of turning parameter, at last, we briefly discuss the de-biased Elastic-net estimator.

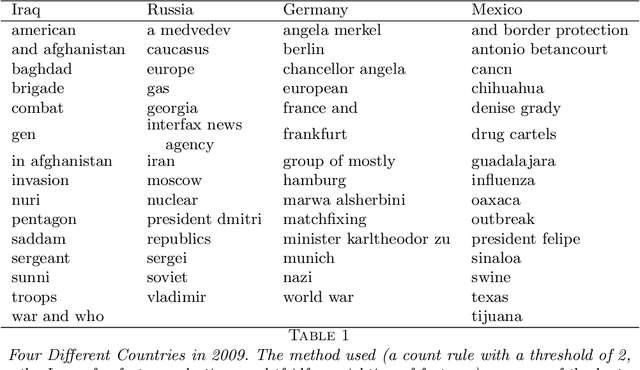
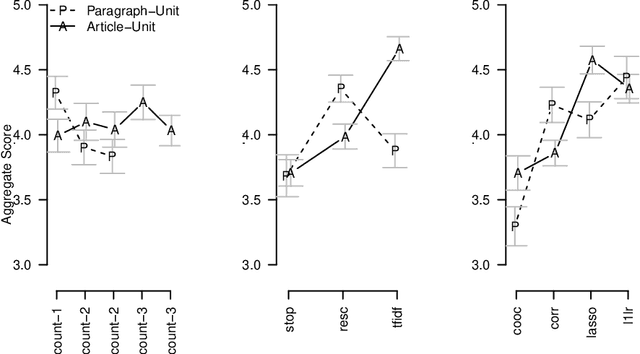
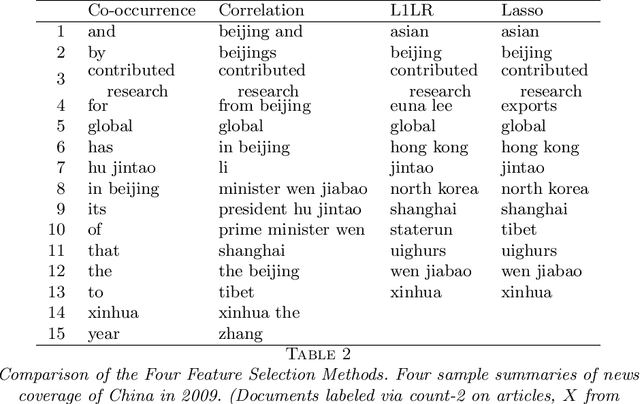
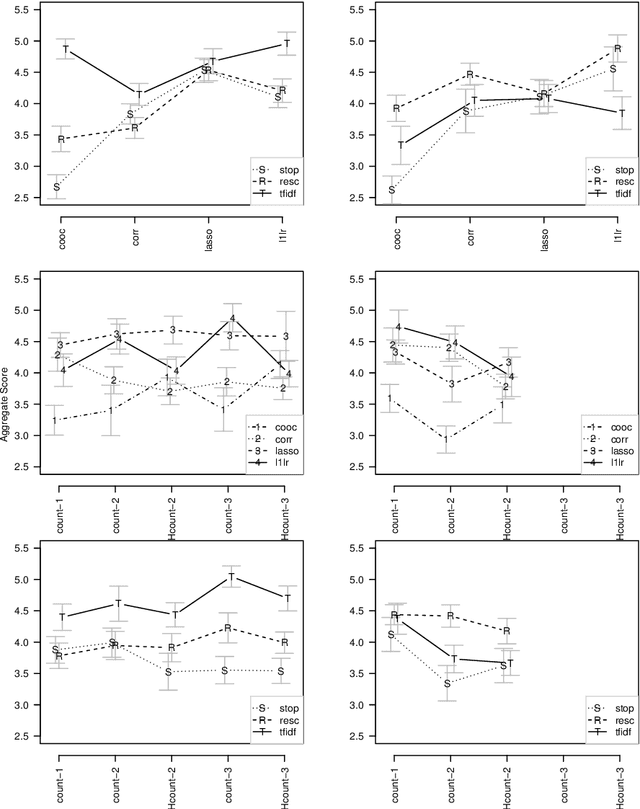
Concise comparative summaries (CCS) of large text corpora with a human experiment

In this paper we propose a general framework for topic-specific summarization of large text corpora and illustrate how it can be used for the analysis of news databases. Our framework, concise comparative summarization (CCS), is built on sparse classification methods. CCS is a lightweight and flexible tool that offers a compromise between simple word frequency based methods currently in wide use and more heavyweight, model-intensive methods such as latent Dirichlet allocation (LDA). We argue that sparse methods have much to offer for text analysis and hope CCS opens the door for a new branch of research in this important field. For a particular topic of interest (e.g., China or energy), CSS automatically labels documents as being either on- or off-topic (usually via keyword search), and then uses sparse classification methods to predict these labels with the high-dimensional counts of all the other words and phrases in the documents. The resulting small set of phrases found as predictive are then harvested as the summary. To validate our tool, we, using news articles from the New York Times international section, designed and conducted a human survey to compare the different summarizers with human understanding. We demonstrate our approach with two case studies, a media analysis of the framing of "Egypt" in the New York Times throughout the Arab Spring and an informal comparison of the New York Times' and Wall Street Journal's coverage of "energy." Overall, we find that the Lasso with $L^2$ normalization can be effectively and usefully used to summarize large corpora, regardless of document size.

Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs

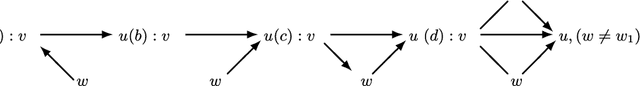
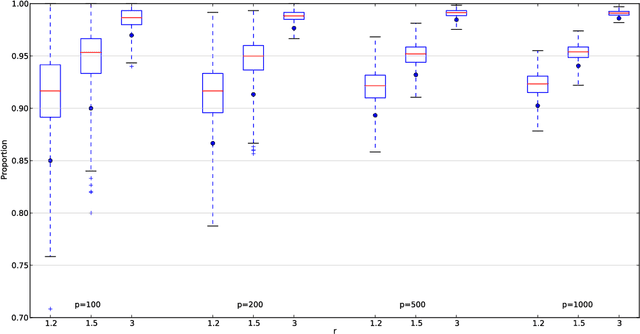
Graphical models are popular statistical tools which are used to represent dependent or causal complex systems. Statistically equivalent causal or directed graphical models are said to belong to a Markov equivalent class. It is of great interest to describe and understand the space of such classes. However, with currently known algorithms, sampling over such classes is only feasible for graphs with fewer than approximately 20 vertices. In this paper, we design reversible irreducible Markov chains on the space of Markov equivalent classes by proposing a perfect set of operators that determine the transitions of the Markov chain. The stationary distribution of a proposed Markov chain has a closed form and can be computed easily. Specifically, we construct a concrete perfect set of operators on sparse Markov equivalence classes by introducing appropriate conditions on each possible operator. Algorithms and their accelerated versions are provided to efficiently generate Markov chains and to explore properties of Markov equivalence classes of sparse directed acyclic graphs (DAGs) with thousands of vertices. We find experimentally that in most Markov equivalence classes of sparse DAGs, (1) most edges are directed, (2) most undirected subgraphs are small and (3) the number of these undirected subgraphs grows approximately linearly with the number of vertices. The article contains supplement arXiv:1303.0632, http://dx.doi.org/10.1214/13-AOS1125SUPP

Supplement to "Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs"

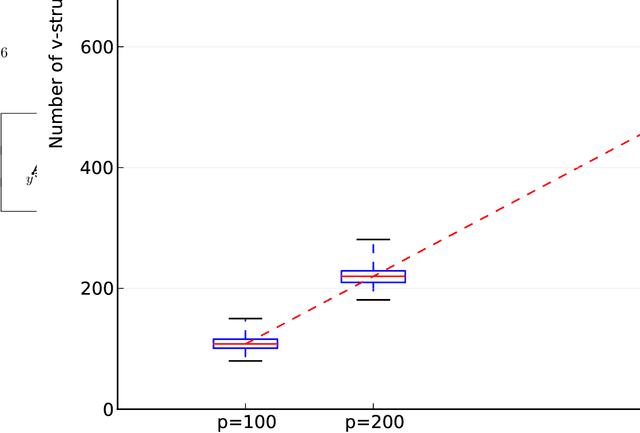
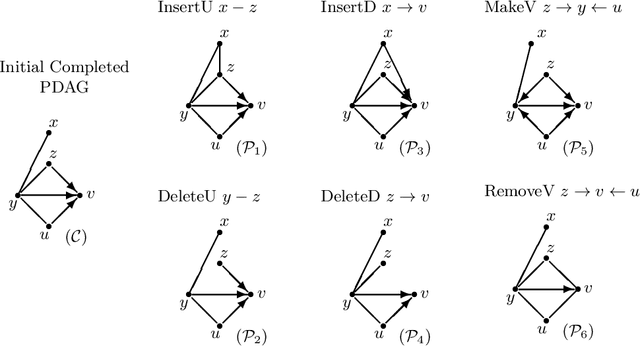
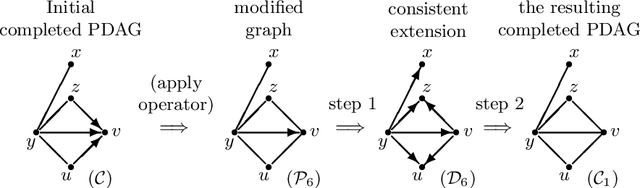
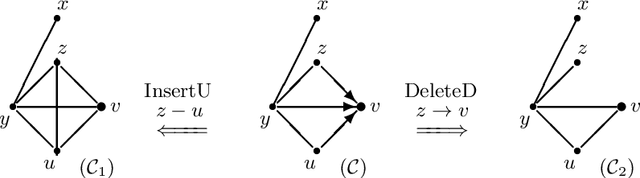
This supplementary material includes three parts: some preliminary results, four examples, an experiment, three new algorithms, and all proofs of the results in the paper "Reversible MCMC on Markov equivalence classes of sparse directed acyclic graphs".

On pattern recovery of the fused Lasso

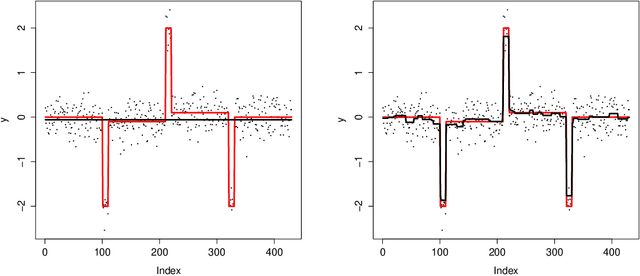
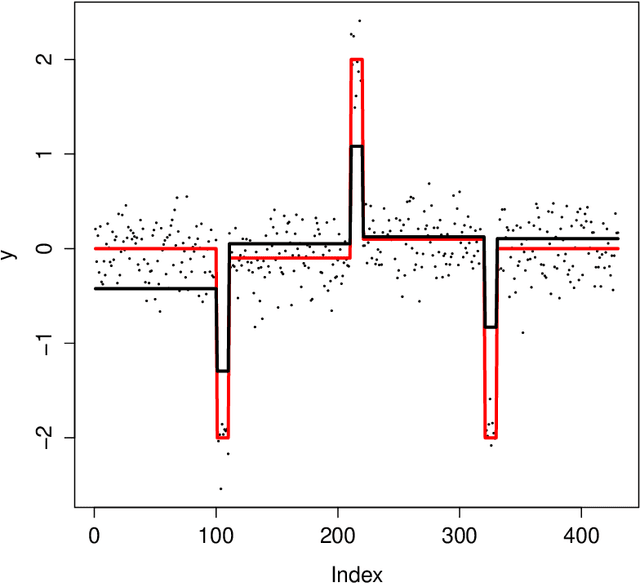
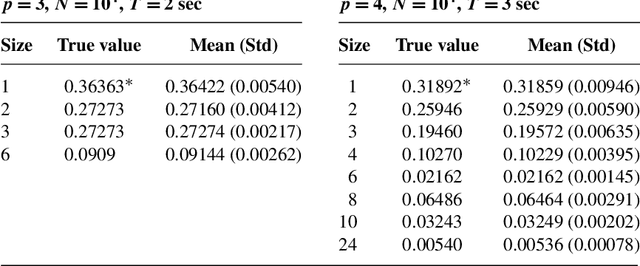
We study the property of the Fused Lasso Signal Approximator (FLSA) for estimating a blocky signal sequence with additive noise. We transform the FLSA to an ordinary Lasso problem. By studying the property of the design matrix in the transformed Lasso problem, we find that the irrepresentable condition might not hold, in which case we show that the FLSA might not be able to recover the signal pattern. We then apply the newly developed preconditioning method -- Puffer Transformation [Jia and Rohe, 2012] on the transformed Lasso problem. We call the new method the preconditioned fused Lasso and we give non-asymptotic results for this method. Results show that when the signal jump strength (signal difference between two neighboring groups) is big and the noise level is small, our preconditioned fused Lasso estimator gives the correct pattern with high probability. Theoretical results give insight on what controls the signal pattern recovery ability -- it is the noise level {instead of} the length of the sequence. Simulations confirm our theorems and show significant improvement of the preconditioned fused Lasso estimator over the vanilla FLSA.

The Lasso under Heteroscedasticity

The performance of the Lasso is well understood under the assumptions of the standard linear model with homoscedastic noise. However, in several applications, the standard model does not describe the important features of the data. This paper examines how the Lasso performs on a non-standard model that is motivated by medical imaging applications. In these applications, the variance of the noise scales linearly with the expectation of the observation. Like all heteroscedastic models, the noise terms in this Poisson-like model are \textit{not} independent of the design matrix. More specifically, this paper studies the sign consistency of the Lasso under a sparse Poisson-like model. In addition to studying sufficient conditions for the sign consistency of the Lasso estimate, this paper also gives necessary conditions for sign consistency. Both sets of conditions are comparable to results for the homoscedastic model, showing that when a measure of the signal to noise ratio is large, the Lasso performs well on both Poisson-like data and homoscedastic data. Simulations reveal that the Lasso performs equally well in terms of model selection performance on both Poisson-like data and homoscedastic data (with properly scaled noise variance), across a range of parameterizations. Taken as a whole, these results suggest that the Lasso is robust to the Poisson-like heteroscedastic noise.