On pattern recovery of the fused Lasso
Paper and Code
Nov 22, 2012

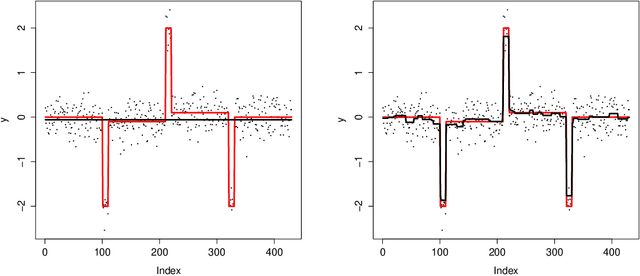
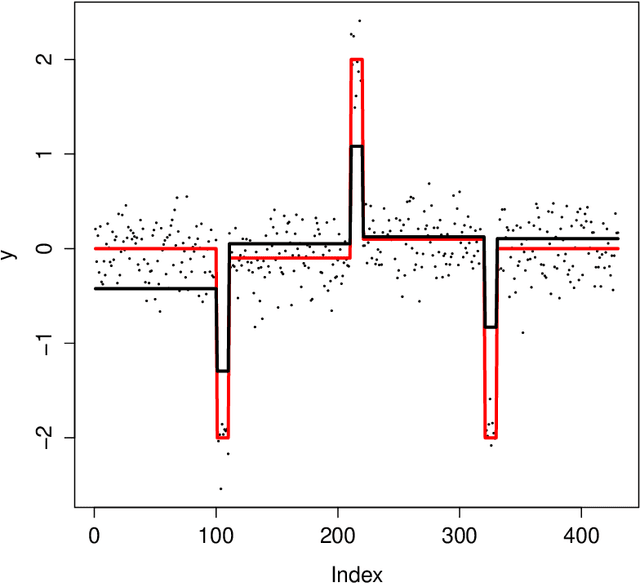
We study the property of the Fused Lasso Signal Approximator (FLSA) for estimating a blocky signal sequence with additive noise. We transform the FLSA to an ordinary Lasso problem. By studying the property of the design matrix in the transformed Lasso problem, we find that the irrepresentable condition might not hold, in which case we show that the FLSA might not be able to recover the signal pattern. We then apply the newly developed preconditioning method -- Puffer Transformation [Jia and Rohe, 2012] on the transformed Lasso problem. We call the new method the preconditioned fused Lasso and we give non-asymptotic results for this method. Results show that when the signal jump strength (signal difference between two neighboring groups) is big and the noise level is small, our preconditioned fused Lasso estimator gives the correct pattern with high probability. Theoretical results give insight on what controls the signal pattern recovery ability -- it is the noise level {instead of} the length of the sequence. Simulations confirm our theorems and show significant improvement of the preconditioned fused Lasso estimator over the vanilla FLSA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge