Junyang Qian
Some methods for heterogeneous treatment effect estimation in high-dimensions
Jul 01, 2017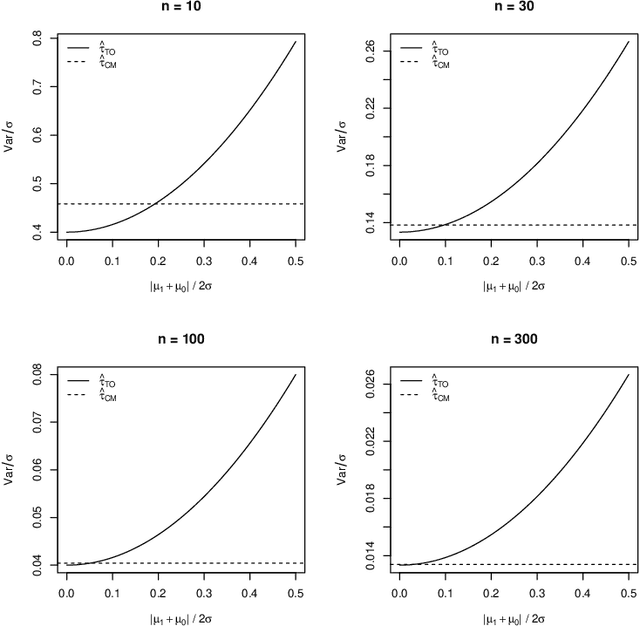
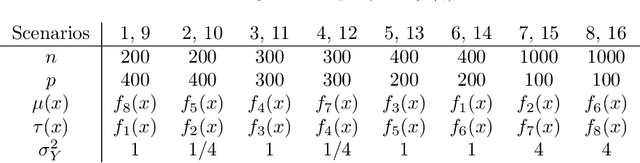
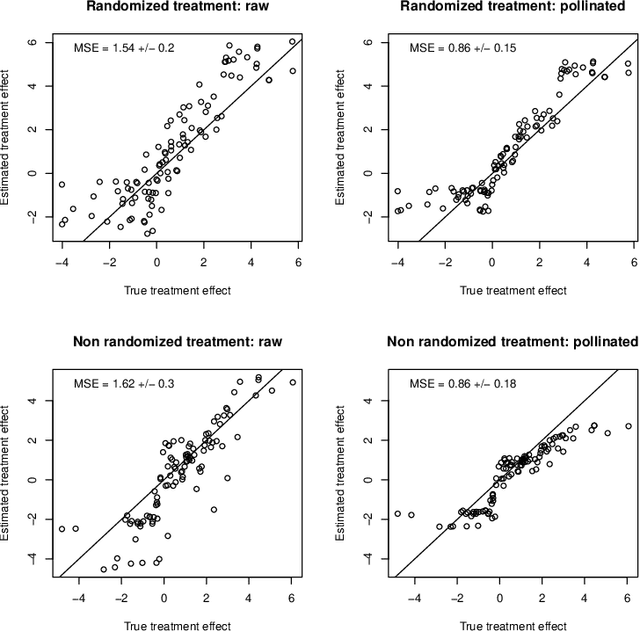
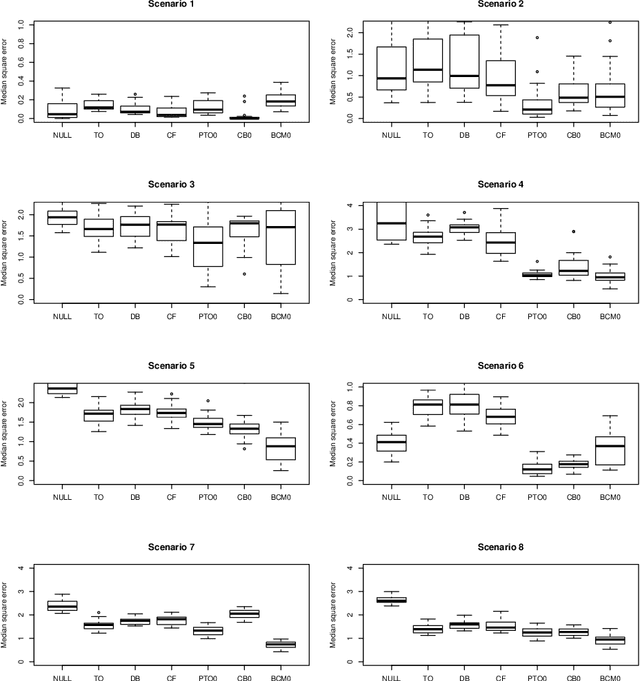
Abstract:When devising a course of treatment for a patient, doctors often have little quantitative evidence on which to base their decisions, beyond their medical education and published clinical trials. Stanford Health Care alone has millions of electronic medical records (EMRs) that are only just recently being leveraged to inform better treatment recommendations. These data present a unique challenge because they are high-dimensional and observational. Our goal is to make personalized treatment recommendations based on the outcomes for past patients similar to a new patient. We propose and analyze three methods for estimating heterogeneous treatment effects using observational data. Our methods perform well in simulations using a wide variety of treatment effect functions, and we present results of applying the two most promising methods to data from The SPRINT Data Analysis Challenge, from a large randomized trial of a treatment for high blood pressure.
Communication-Efficient False Discovery Rate Control via Knockoff Aggregation
Nov 09, 2015


Abstract:The false discovery rate (FDR)---the expected fraction of spurious discoveries among all the discoveries---provides a popular statistical assessment of the reproducibility of scientific studies in various disciplines. In this work, we introduce a new method for controlling the FDR in meta-analysis of many decentralized linear models. Our method targets the scenario where many research groups---possibly the number of which is random---are independently testing a common set of hypotheses and then sending summary statistics to a coordinating center in an online manner. Built on the knockoffs framework introduced by Barber and Candes (2015), our procedure starts by applying the knockoff filter to each linear model and then aggregates the summary statistics via one-shot communication in a novel way. This method gives exact FDR control non-asymptotically without any knowledge of the noise variances or making any assumption about sparsity of the signal. In certain settings, it has a communication complexity that is optimal up to a logarithmic factor.
On pattern recovery of the fused Lasso
Nov 22, 2012

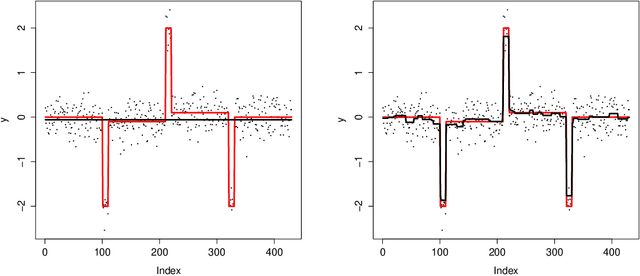
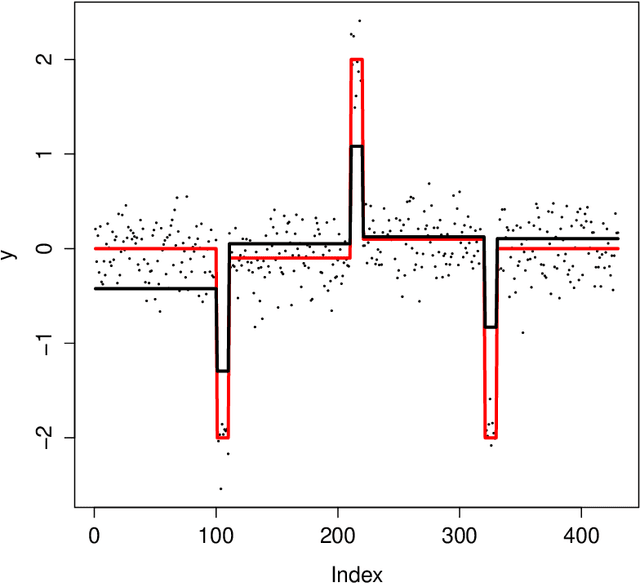
Abstract:We study the property of the Fused Lasso Signal Approximator (FLSA) for estimating a blocky signal sequence with additive noise. We transform the FLSA to an ordinary Lasso problem. By studying the property of the design matrix in the transformed Lasso problem, we find that the irrepresentable condition might not hold, in which case we show that the FLSA might not be able to recover the signal pattern. We then apply the newly developed preconditioning method -- Puffer Transformation [Jia and Rohe, 2012] on the transformed Lasso problem. We call the new method the preconditioned fused Lasso and we give non-asymptotic results for this method. Results show that when the signal jump strength (signal difference between two neighboring groups) is big and the noise level is small, our preconditioned fused Lasso estimator gives the correct pattern with high probability. Theoretical results give insight on what controls the signal pattern recovery ability -- it is the noise level {instead of} the length of the sequence. Simulations confirm our theorems and show significant improvement of the preconditioned fused Lasso estimator over the vanilla FLSA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge