Targeted Deep Architectures: A TMLE-Based Framework for Robust Causal Inference in Neural Networks

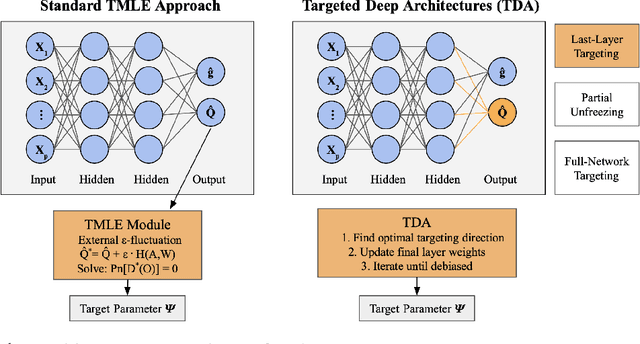
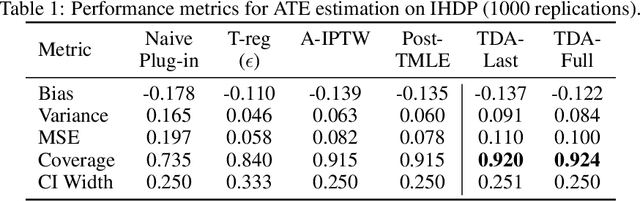
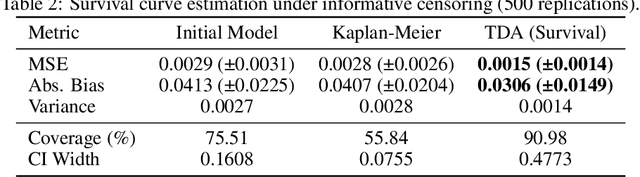
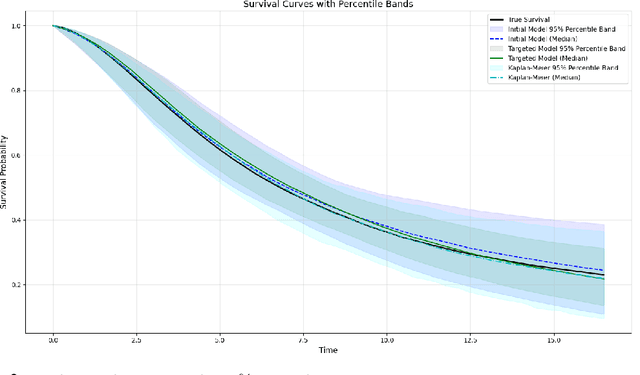
Modern deep neural networks are powerful predictive tools yet often lack valid inference for causal parameters, such as treatment effects or entire survival curves. While frameworks like Double Machine Learning (DML) and Targeted Maximum Likelihood Estimation (TMLE) can debias machine-learning fits, existing neural implementations either rely on "targeted losses" that do not guarantee solving the efficient influence function equation or computationally expensive post-hoc "fluctuations" for multi-parameter settings. We propose Targeted Deep Architectures (TDA), a new framework that embeds TMLE directly into the network's parameter space with no restrictions on the backbone architecture. Specifically, TDA partitions model parameters - freezing all but a small "targeting" subset - and iteratively updates them along a targeting gradient, derived from projecting the influence functions onto the span of the gradients of the loss with respect to weights. This procedure yields plug-in estimates that remove first-order bias and produce asymptotically valid confidence intervals. Crucially, TDA easily extends to multi-dimensional causal estimands (e.g., entire survival curves) by merging separate targeting gradients into a single universal targeting update. Theoretically, TDA inherits classical TMLE properties, including double robustness and semiparametric efficiency. Empirically, on the benchmark IHDP dataset (average treatment effects) and simulated survival data with informative censoring, TDA reduces bias and improves coverage relative to both standard neural-network estimators and prior post-hoc approaches. In doing so, TDA establishes a direct, scalable pathway toward rigorous causal inference within modern deep architectures for complex multi-parameter targets.

RieszBoost: Gradient Boosting for Riesz Regression

Answering causal questions often involves estimating linear functionals of conditional expectations, such as the average treatment effect or the effect of a longitudinal modified treatment policy. By the Riesz representation theorem, these functionals can be expressed as the expected product of the conditional expectation of the outcome and the Riesz representer, a key component in doubly robust estimation methods. Traditionally, the Riesz representer is estimated indirectly by deriving its explicit analytical form, estimating its components, and substituting these estimates into the known form (e.g., the inverse propensity score). However, deriving or estimating the analytical form can be challenging, and substitution methods are often sensitive to practical positivity violations, leading to higher variance and wider confidence intervals. In this paper, we propose a novel gradient boosting algorithm to directly estimate the Riesz representer without requiring its explicit analytical form. This method is particularly suited for tabular data, offering a flexible, nonparametric, and computationally efficient alternative to existing methods for Riesz regression. Through simulation studies, we demonstrate that our algorithm performs on par with or better than indirect estimation techniques across a range of functionals, providing a user-friendly and robust solution for estimating causal quantities.

Highly Adaptive Ridge

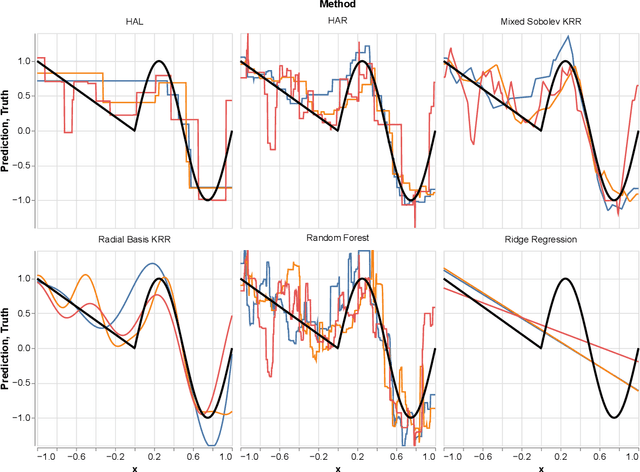
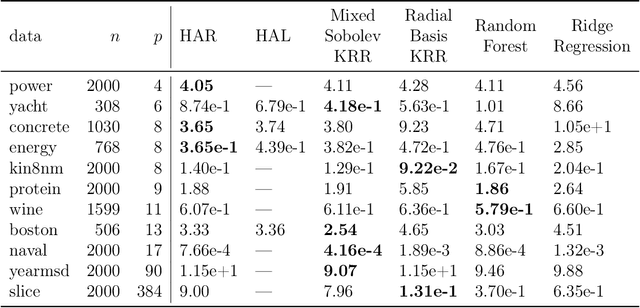
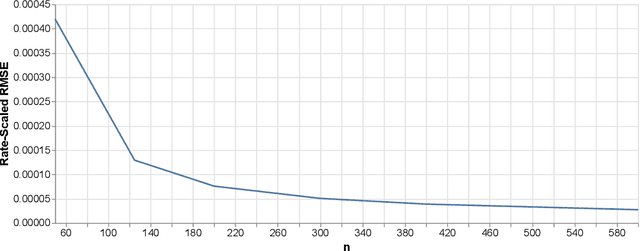
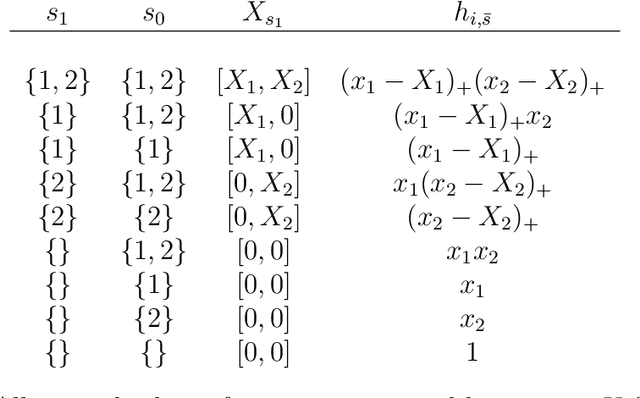
In this paper we propose the Highly Adaptive Ridge (HAR): a regression method that achieves a $n^{-1/3}$ dimension-free L2 convergence rate in the class of right-continuous functions with square-integrable sectional derivatives. This is a large nonparametric function class that is particularly appropriate for tabular data. HAR is exactly kernel ridge regression with a specific data-adaptive kernel based on a saturated zero-order tensor-product spline basis expansion. We use simulation and real data to confirm our theory. We demonstrate empirical performance better than state-of-the-art algorithms for small datasets in particular.

The Selectively Adaptive Lasso

Machine learning regression methods allow estimation of functions without unrealistic parametric assumptions. Although they can perform exceptionally in prediction error, most lack theoretical convergence rates necessary for semi-parametric efficient estimation (e.g. TMLE, AIPW) of parameters like average treatment effects. The Highly Adaptive Lasso (HAL) is the only regression method proven to converge quickly enough for a meaningfully large class of functions, independent of the dimensionality of the predictors. Unfortunately, HAL is not computationally scalable. In this paper we build upon the theory of HAL to construct the Selectively Adaptive Lasso (SAL), a new algorithm which retains HAL's dimension-free, nonparametric convergence rate but which also scales computationally to massive datasets. To accomplish this, we prove some general theoretical results pertaining to empirical loss minimization in nested Donsker classes. Our resulting algorithm is a form of gradient tree boosting with an adaptive learning rate, which makes it fast and trivial to implement with off-the-shelf software. Finally, we show that our algorithm retains the performance of standard gradient boosting on a diverse group of real-world datasets. SAL makes semi-parametric efficient estimators practically possible and theoretically justifiable in many big data settings.

Multivariate Probabilistic Regression with Natural Gradient Boosting

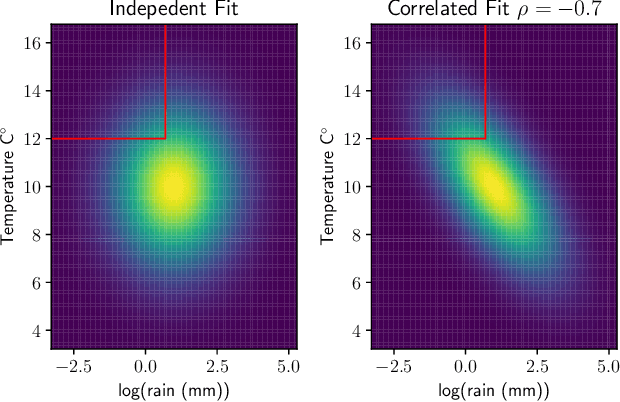
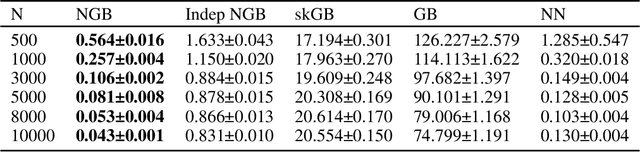
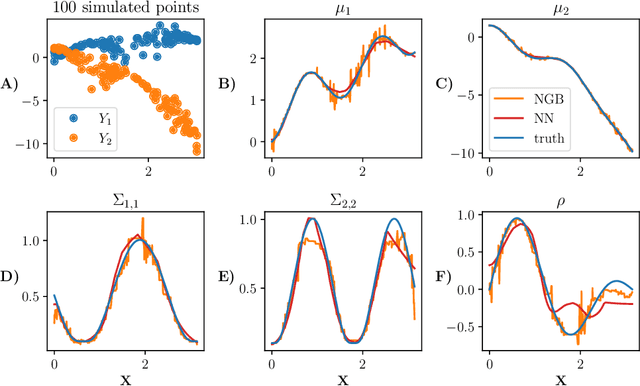
Many single-target regression problems require estimates of uncertainty along with the point predictions. Probabilistic regression algorithms are well-suited for these tasks. However, the options are much more limited when the prediction target is multivariate and a joint measure of uncertainty is required. For example, in predicting a 2D velocity vector a joint uncertainty would quantify the probability of any vector in the plane, which would be more expressive than two separate uncertainties on the x- and y- components. To enable joint probabilistic regression, we propose a Natural Gradient Boosting (NGBoost) approach based on nonparametrically modeling the conditional parameters of the multivariate predictive distribution. Our method is robust, works out-of-the-box without extensive tuning, is modular with respect to the assumed target distribution, and performs competitively in comparison to existing approaches. We demonstrate these claims in simulation and with a case study predicting two-dimensional oceanographic velocity data. An implementation of our method is available at https://github.com/stanfordmlgroup/ngboost.

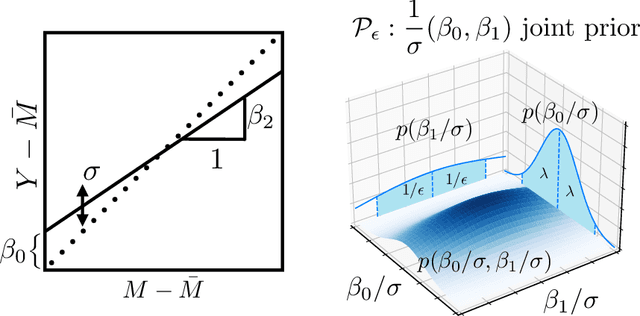
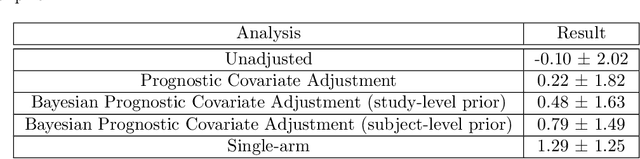
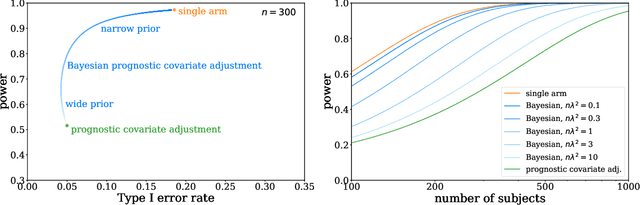
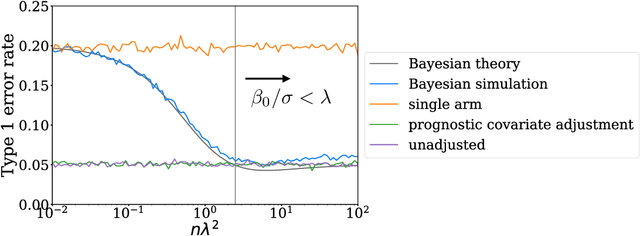
Bayesian prognostic covariate adjustment

Historical data about disease outcomes can be integrated into the analysis of clinical trials in many ways. We build on existing literature that uses prognostic scores from a predictive model to increase the efficiency of treatment effect estimates via covariate adjustment. Here we go further, utilizing a Bayesian framework that combines prognostic covariate adjustment with an empirical prior distribution learned from the predictive performances of the prognostic model on past trials. The Bayesian approach interpolates between prognostic covariate adjustment with strict type I error control when the prior is diffuse, and a single-arm trial when the prior is sharply peaked. This method is shown theoretically to offer a substantial increase in statistical power, while limiting the type I error rate under reasonable conditions. We demonstrate the utility of our method in simulations and with an analysis of a past Alzheimer's disease clinical trial.

Increasing the efficiency of randomized trial estimates via linear adjustment for a prognostic score

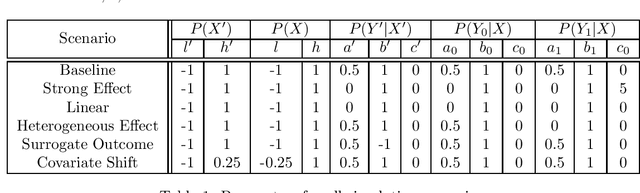
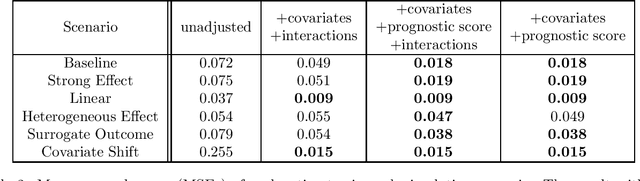
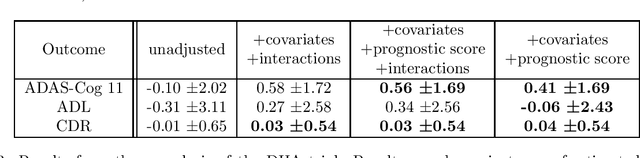
Estimating causal effects from randomized experiments is central to clinical research. Reducing the statistical uncertainty in these analyses is an important objective for statisticians. Registries, prior trials, and health records constitute a growing compendium of historical data on patients under standard-of-care conditions that may be exploitable to this end. However, most methods for historical borrowing achieve reductions in variance by sacrificing strict type-I error rate control. Here, we propose a use of historical data that exploits linear covariate adjustment to improve the efficiency of trial analyses without incurring bias. Specifically, we train a prognostic model on the historical data, then estimate the treatment effect using a linear regression while adjusting for the trial subjects' predicted outcomes (their prognostic scores). We prove that, under certain conditions, this prognostic covariate adjustment procedure attains the minimum variance possible among a large class of estimators. When those conditions are not met, prognostic covariate adjustment is still more efficient than raw covariate adjustment and the gain in efficiency is proportional to a measure of the predictive accuracy of the prognostic model. We demonstrate the approach using simulations and a reanalysis of an Alzheimer's Disease clinical trial and observe meaningful reductions in mean-squared error and the estimated variance. Lastly, we provide a simplified formula for asymptotic variance that enables power and sample size calculations that account for the gains from the prognostic model for clinical trial design.

Performance metrics for intervention-triggering prediction models do not reflect an expected reduction in outcomes from using the model

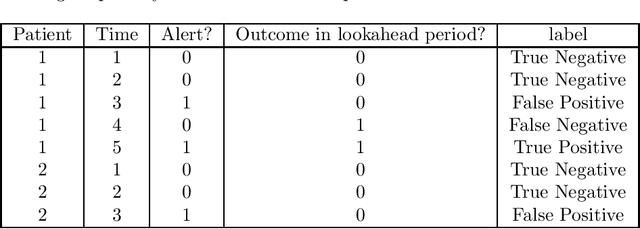
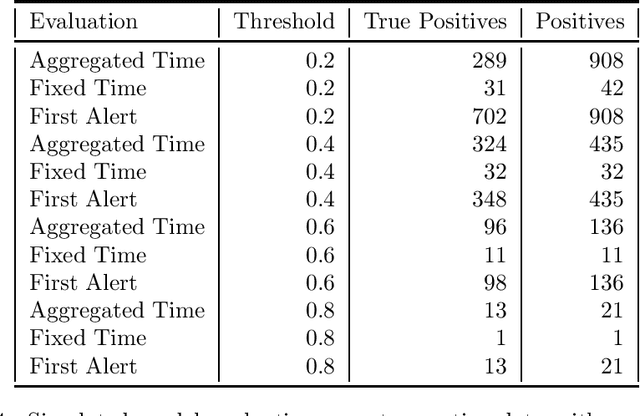
Clinical researchers often select among and evaluate risk prediction models using standard machine learning metrics based on confusion matrices. However, if these models are used to allocate interventions to patients, standard metrics calculated from retrospective data are only related to model utility (in terms of reductions in outcomes) under certain assumptions. When predictions are delivered repeatedly throughout time (e.g. in a patient encounter), the relationship between standard metrics and utility is further complicated. Several kinds of evaluations have been used in the literature, but it has not been clear what the target of estimation is in each evaluation. We synthesize these approaches, determine what is being estimated in each of them, and discuss under what assumptions those estimates are valid. We demonstrate our insights using simulated data as well as real data used in the design of an early warning system. Our theoretical and empirical results show that evaluations without interventional data either do not estimate meaningful quantities, require strong assumptions, or are limited to estimating best-case scenario bounds.

NGBoost: Natural Gradient Boosting for Probabilistic Prediction

We present Natural Gradient Boosting (NGBoost), an algorithm which brings probabilistic prediction capability to gradient boosting in a generic way. Predictive uncertainty estimation is crucial in many applications such as healthcare and weather forecasting. Probabilistic prediction, which is the approach where the model outputs a full probability distribution over the entire outcome space, is a natural way to quantify those uncertainties. Gradient Boosting Machines have been widely successful in prediction tasks on structured input data, but a simple boosting solution for probabilistic prediction of real valued outputs is yet to be made. NGBoost is a gradient boosting approach which uses the \emph{Natural Gradient} to address technical challenges that makes generic probabilistic prediction hard with existing gradient boosting methods. Our approach is modular with respect to the choice of base learner, probability distribution, and scoring rule. We show empirically on several regression datasets that NGBoost provides competitive predictive performance of both uncertainty estimates and traditional metrics.

A comparison of methods for model selection when estimating individual treatment effects

Practitioners in medicine, business, political science, and other fields are increasingly aware that decisions should be personalized to each patient, customer, or voter. A given treatment (e.g. a drug or advertisement) should be administered only to those who will respond most positively, and certainly not to those who will be harmed by it. Individual-level treatment effects can be estimated with tools adapted from machine learning, but different models can yield contradictory estimates. Unlike risk prediction models, however, treatment effect models cannot be easily evaluated against each other using a held-out test set because the true treatment effect itself is never directly observed. Besides outcome prediction accuracy, several metrics that can leverage held-out data to evaluate treatment effects models have been proposed, but they are not widely used. We provide a didactic framework that elucidates the relationships between the different approaches and compare them all using a variety of simulations of both randomized and observational data. Our results show that researchers estimating heterogenous treatment effects need not limit themselves to a single model-fitting algorithm. Instead of relying on a single method, multiple models fit by a diverse set of algorithms should be evaluated against each other using an objective function learned from the validation set. The model minimizing that objective should be used for estimating the individual treatment effect for future individuals.