Multivariate Probabilistic Regression with Natural Gradient Boosting

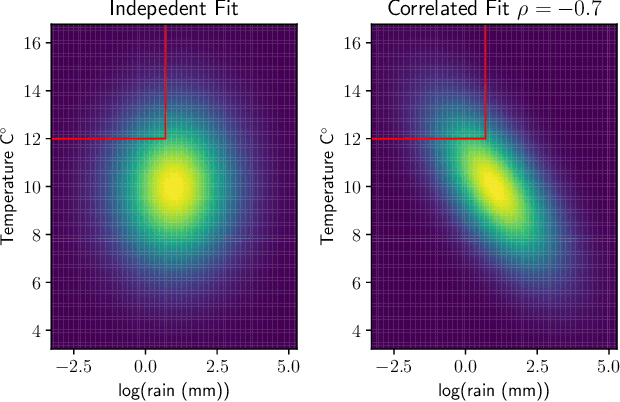
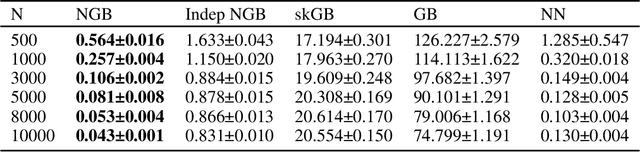
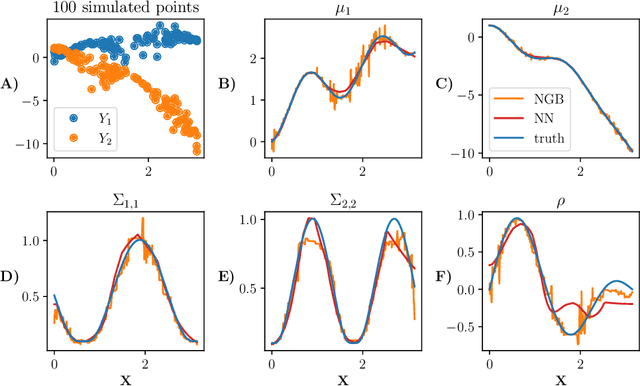
Many single-target regression problems require estimates of uncertainty along with the point predictions. Probabilistic regression algorithms are well-suited for these tasks. However, the options are much more limited when the prediction target is multivariate and a joint measure of uncertainty is required. For example, in predicting a 2D velocity vector a joint uncertainty would quantify the probability of any vector in the plane, which would be more expressive than two separate uncertainties on the x- and y- components. To enable joint probabilistic regression, we propose a Natural Gradient Boosting (NGBoost) approach based on nonparametrically modeling the conditional parameters of the multivariate predictive distribution. Our method is robust, works out-of-the-box without extensive tuning, is modular with respect to the assumed target distribution, and performs competitively in comparison to existing approaches. We demonstrate these claims in simulation and with a case study predicting two-dimensional oceanographic velocity data. An implementation of our method is available at https://github.com/stanfordmlgroup/ngboost.

Efficient Parameter Estimation of Sampled Random Fields

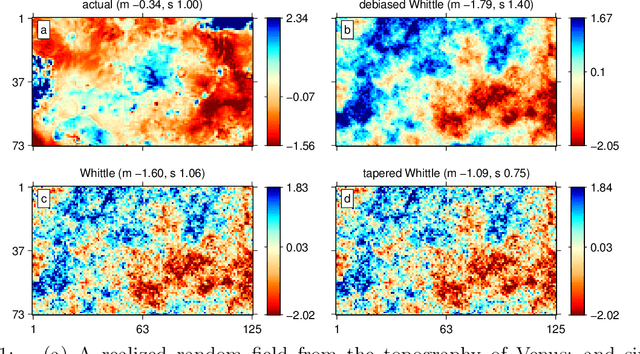
We provide a computationally and statistically efficient method for estimating the parameters of a stochastic Gaussian model observed on a spatial grid, which need not be rectangular. Standard methods are plagued by computational intractability, where designing methods that can be implemented for realistically sized problems has been an issue for a long time. This has motivated the use of the Fourier Transform and the Whittle likelihood approximation. The challenge of frequency-domain methods is to determine and account for observational boundary effects, missing data, and the shape of the observed spatial grid. In this paper we address these effects explicitly by proposing a new quasi-likelihood estimator. We prove consistency and asymptotic normality of our estimator, and show that the proposed method solves boundary issues with Whittle estimation for finite samples, yielding parameter estimates with significantly reduced bias and error. We demonstrate the effectiveness of our method for incomplete lattices, in comparison to other recent methods. Finally, we apply our method to estimate the parameters of a Mat\'ern process used to model data from Venus' topography.

Smoothing and Interpolating Noisy GPS Data with Smoothing Splines

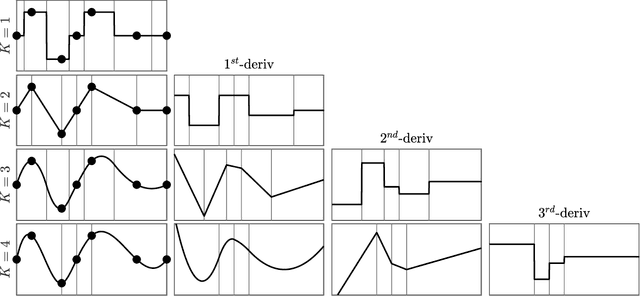
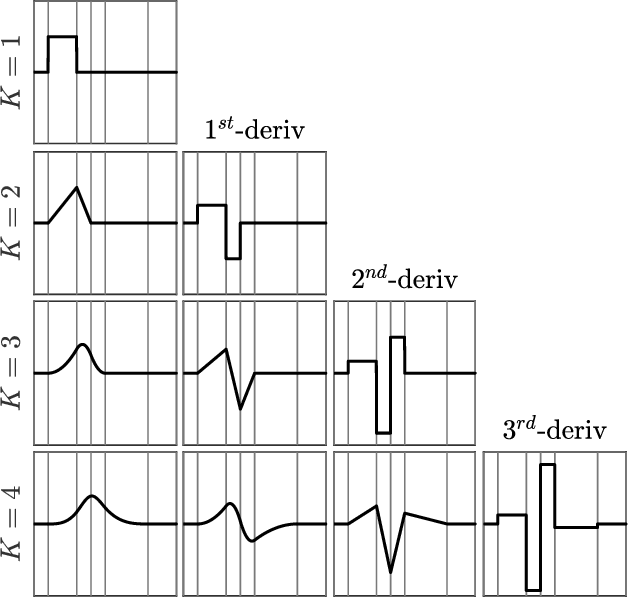
A comprehensive methodology is provided for smoothing noisy, irregularly sampled data with non-Gaussian noise using smoothing splines. We demonstrate how the spline order and tension parameter can be chosen \emph{a priori} from physical reasoning. We also show how to allow for non-Gaussian noise and outliers which are typical in GPS signals. We demonstrate the effectiveness of our methods on GPS trajectory data obtained from oceanographic floating instruments known as drifters.

The De-Biased Whittle Likelihood

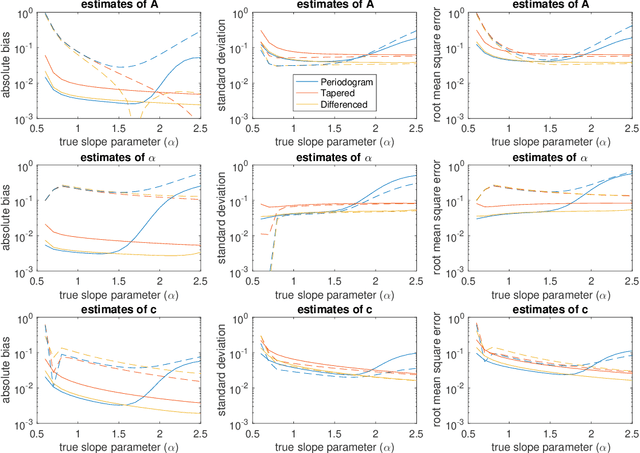
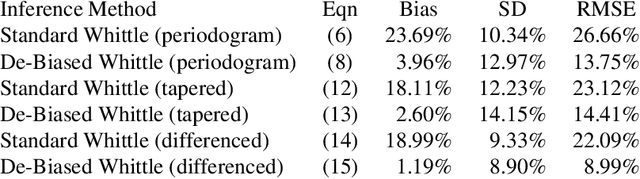
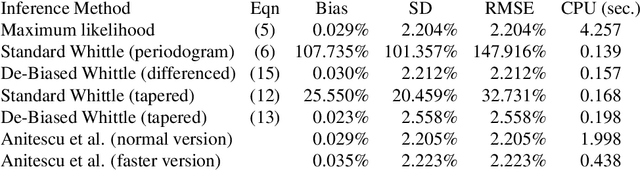
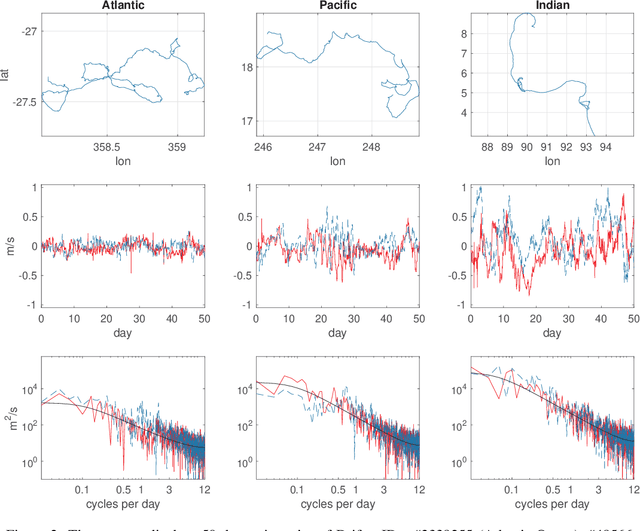
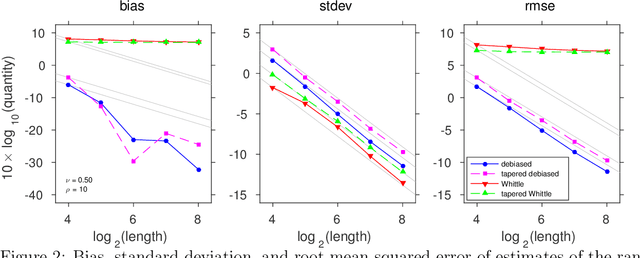
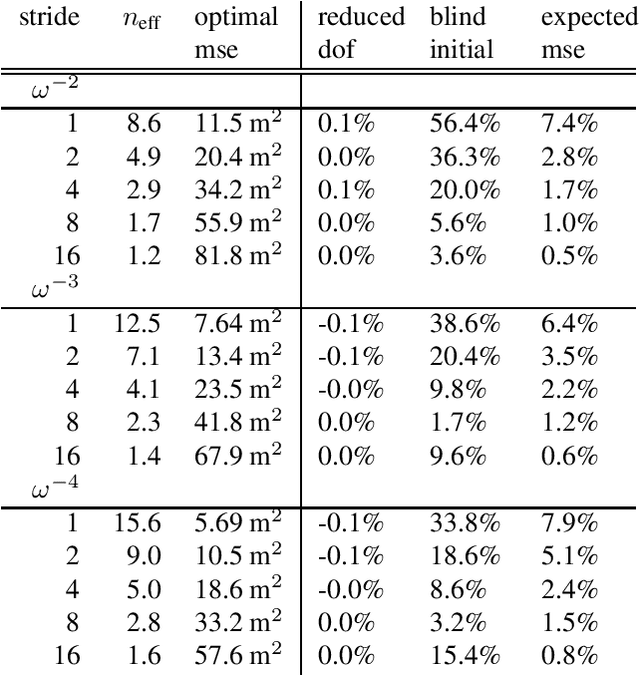
The Whittle likelihood is a widely used and computationally efficient pseudo-likelihood. However, it is known to produce biased parameter estimates for large classes of models. We propose a method for de-biasing Whittle estimates for second-order stationary stochastic processes. The de-biased Whittle likelihood can be computed in the same $\mathcal{O}(n\log n)$ operations as the standard approach. We demonstrate the superior performance of the method in simulation studies and in application to a large-scale oceanographic dataset, where in both cases the de-biased approach reduces bias by up to two orders of magnitude, achieving estimates that are close to exact maximum likelihood, at a fraction of the computational cost. We prove that the method yields estimates that are consistent at an optimal convergence rate of $n^{-1/2}$, under weaker assumptions than standard theory, where we do not require that the power spectral density is continuous in frequency. We describe how the method can be easily combined with standard methods of bias reduction, such as tapering and differencing, to further reduce bias in parameter estimates.

Exact Simulation of Noncircular or Improper Complex-Valued Stationary Gaussian Processes using Circulant Embedding

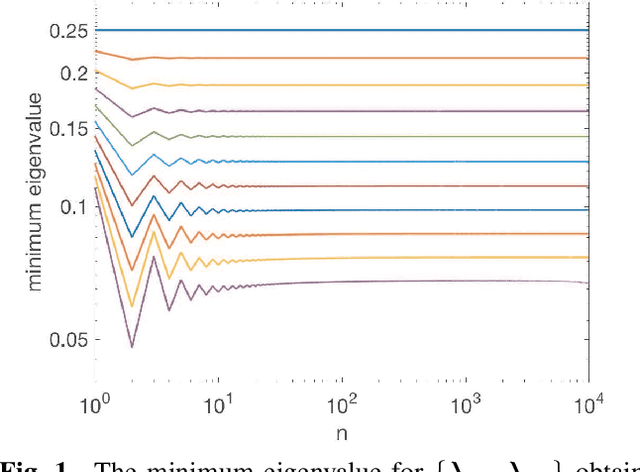
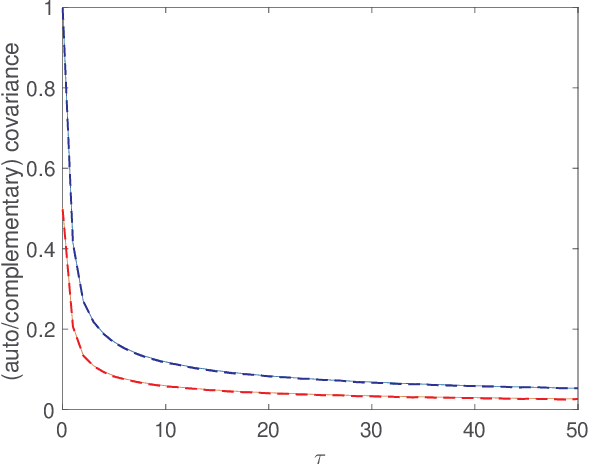
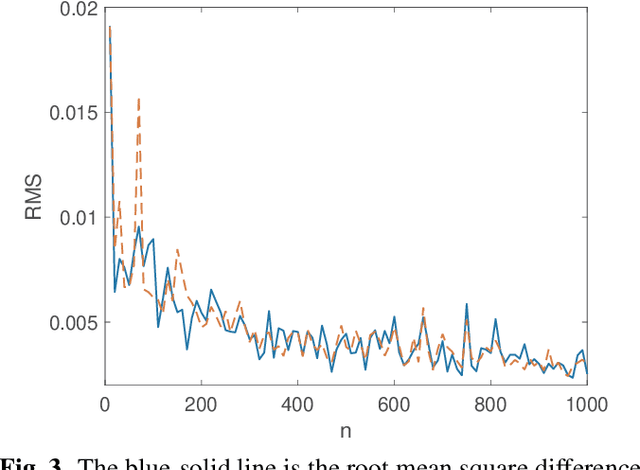
This paper provides an algorithm for simulating improper (or noncircular) complex-valued stationary Gaussian processes. The technique utilizes recently developed methods for multivariate Gaussian processes from the circulant embedding literature. The method can be performed in $\mathcal{O}(n\log_2 n)$ operations, where $n$ is the length of the desired sequence. The method is exact, except when eigenvalues of prescribed circulant matrices are negative. We evaluate the performance of the algorithm empirically, and provide a practical example where the method is guaranteed to be exact for all $n$, with an improper fractional Gaussian noise process.

Frequency-Domain Stochastic Modeling of Stationary Bivariate or Complex-Valued Signals

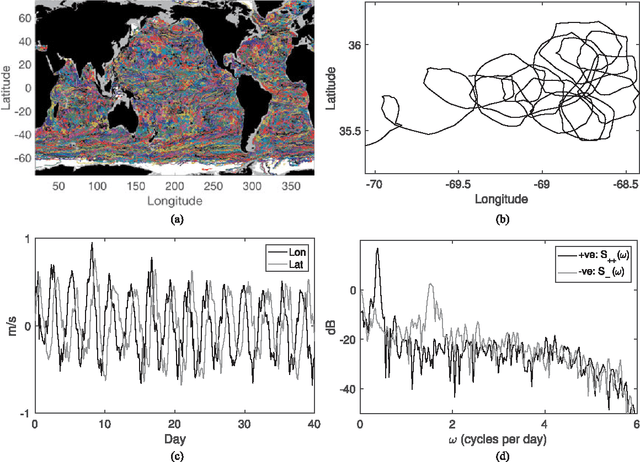
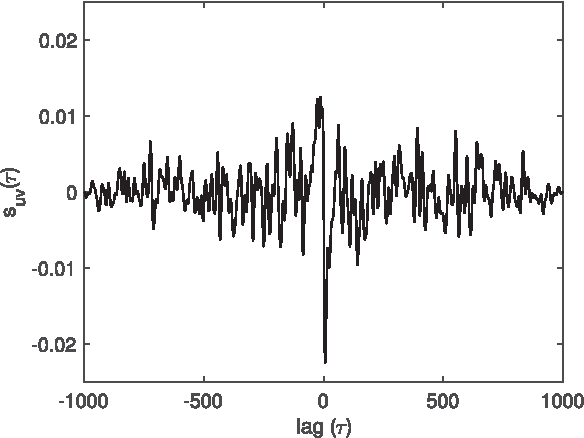
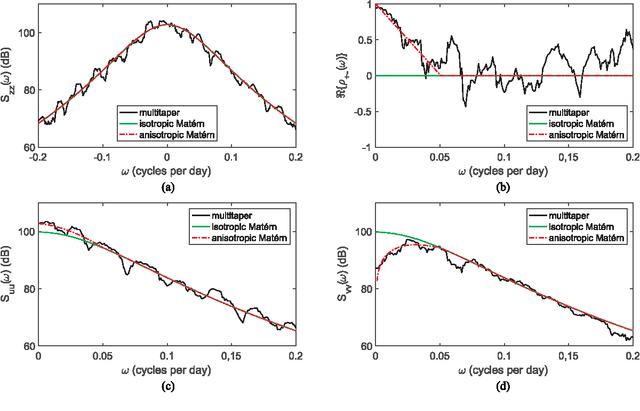
There are three equivalent ways of representing two jointly observed real-valued signals: as a bivariate vector signal, as a single complex-valued signal, or as two analytic signals known as the rotary components. Each representation has unique advantages depending on the system of interest and the application goals. In this paper we provide a joint framework for all three representations in the context of frequency-domain stochastic modeling. This framework allows us to extend many established statistical procedures for bivariate vector time series to complex-valued and rotary representations. These include procedures for parametrically modeling signal coherence, estimating model parameters using the Whittle likelihood, performing semi-parametric modeling, and choosing between classes of nested models using model choice. We also provide a new method of testing for impropriety in complex-valued signals, which tests for noncircular or anisotropic second-order statistical structure when the signal is represented in the complex plane. Finally, we demonstrate the usefulness of our methodology in capturing the anisotropic structure of signals observed from fluid dynamic simulations of turbulence.

Automated Planning in Repeated Adversarial Games

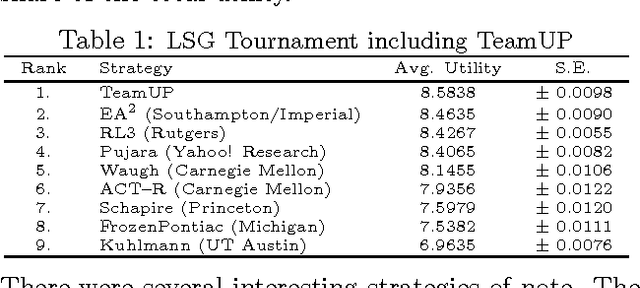
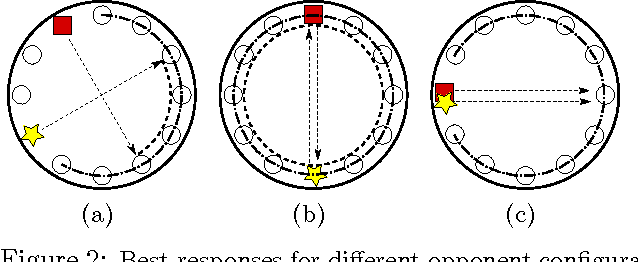
Game theory's prescriptive power typically relies on full rationality and/or self-play interactions. In contrast, this work sets aside these fundamental premises and focuses instead on heterogeneous autonomous interactions between two or more agents. Specifically, we introduce a new and concise representation for repeated adversarial (constant-sum) games that highlight the necessary features that enable an automated planing agent to reason about how to score above the game's Nash equilibrium, when facing heterogeneous adversaries. To this end, we present TeamUP, a model-based RL algorithm designed for learning and planning such an abstraction. In essence, it is somewhat similar to R-max with a cleverly engineered reward shaping that treats exploration as an adversarial optimization problem. In practice, it attempts to find an ally with which to tacitly collude (in more than two-player games) and then collaborates on a joint plan of actions that can consistently score a high utility in adversarial repeated games. We use the inaugural Lemonade Stand Game Tournament to demonstrate the effectiveness of our approach, and find that TeamUP is the best performing agent, demoting the Tournament's actual winning strategy into second place. In our experimental analysis, we show hat our strategy successfully and consistently builds collaborations with many different heterogeneous (and sometimes very sophisticated) adversaries.