Jonathan M. Lilly
The De-Biased Whittle Likelihood
Sep 12, 2018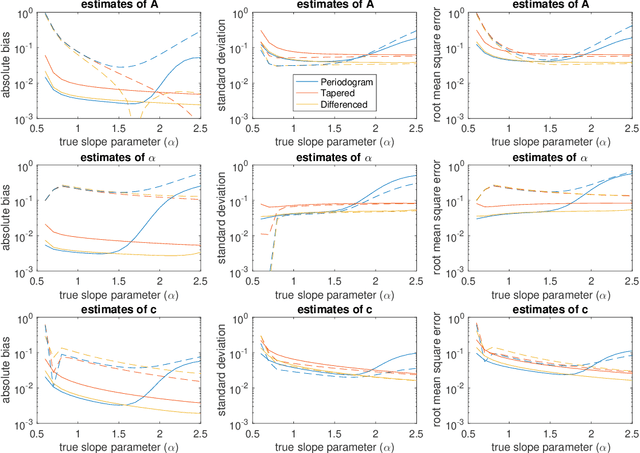
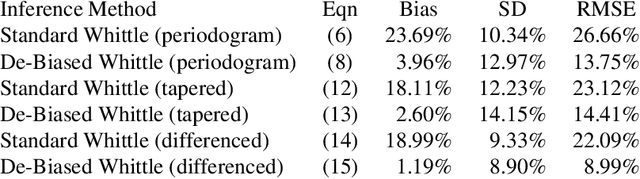
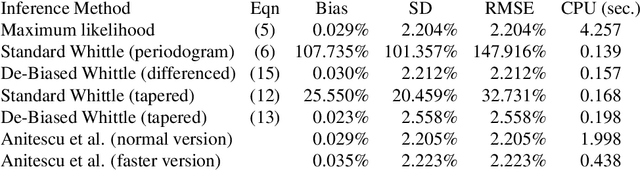
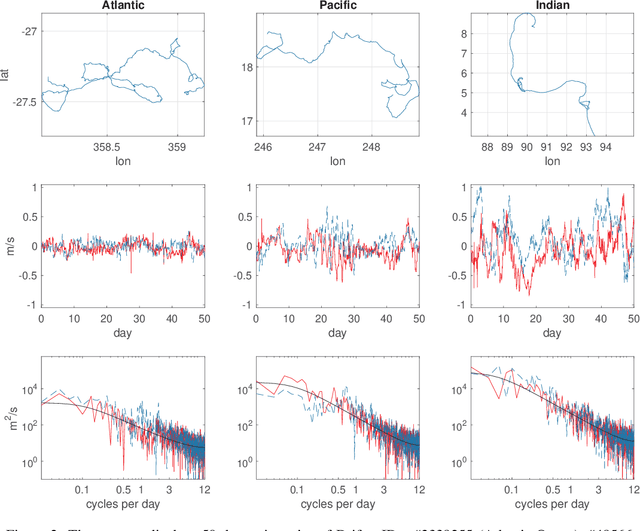
Abstract:The Whittle likelihood is a widely used and computationally efficient pseudo-likelihood. However, it is known to produce biased parameter estimates for large classes of models. We propose a method for de-biasing Whittle estimates for second-order stationary stochastic processes. The de-biased Whittle likelihood can be computed in the same $\mathcal{O}(n\log n)$ operations as the standard approach. We demonstrate the superior performance of the method in simulation studies and in application to a large-scale oceanographic dataset, where in both cases the de-biased approach reduces bias by up to two orders of magnitude, achieving estimates that are close to exact maximum likelihood, at a fraction of the computational cost. We prove that the method yields estimates that are consistent at an optimal convergence rate of $n^{-1/2}$, under weaker assumptions than standard theory, where we do not require that the power spectral density is continuous in frequency. We describe how the method can be easily combined with standard methods of bias reduction, such as tapering and differencing, to further reduce bias in parameter estimates.
Frequency-Domain Stochastic Modeling of Stationary Bivariate or Complex-Valued Signals
Mar 15, 2017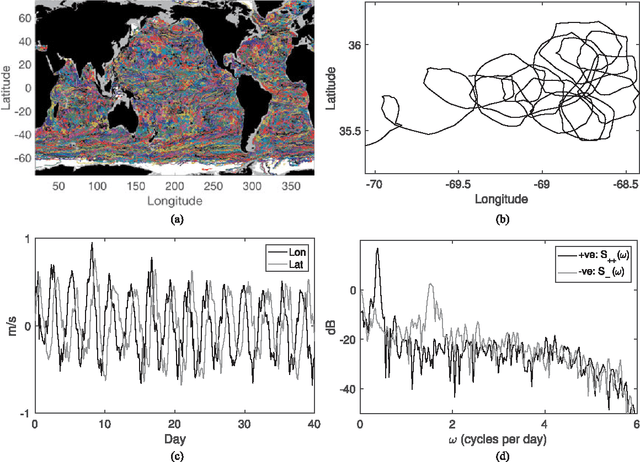

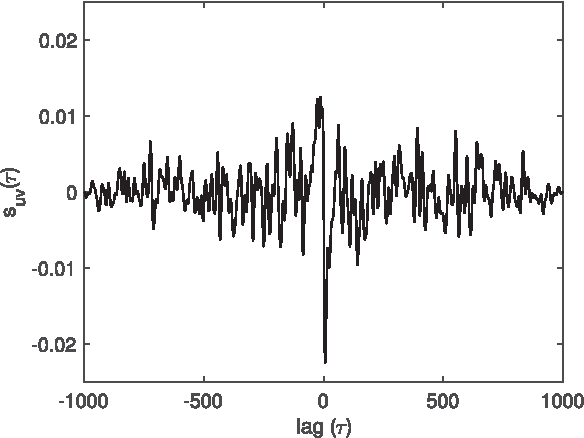
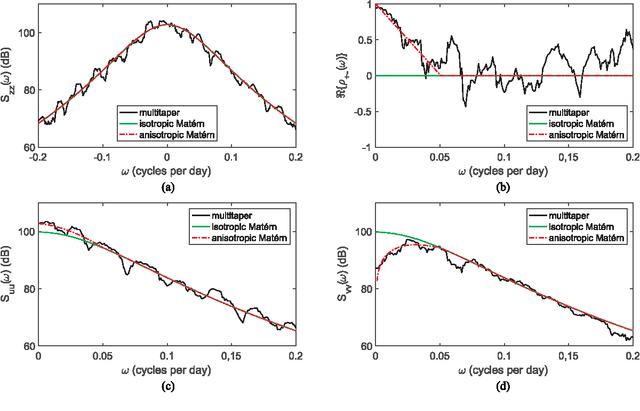
Abstract:There are three equivalent ways of representing two jointly observed real-valued signals: as a bivariate vector signal, as a single complex-valued signal, or as two analytic signals known as the rotary components. Each representation has unique advantages depending on the system of interest and the application goals. In this paper we provide a joint framework for all three representations in the context of frequency-domain stochastic modeling. This framework allows us to extend many established statistical procedures for bivariate vector time series to complex-valued and rotary representations. These include procedures for parametrically modeling signal coherence, estimating model parameters using the Whittle likelihood, performing semi-parametric modeling, and choosing between classes of nested models using model choice. We also provide a new method of testing for impropriety in complex-valued signals, which tests for noncircular or anisotropic second-order statistical structure when the signal is represented in the complex plane. Finally, we demonstrate the usefulness of our methodology in capturing the anisotropic structure of signals observed from fluid dynamic simulations of turbulence.
* To appear in IEEE Transactions on Signal Processing
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge