Frequency-Domain Stochastic Modeling of Stationary Bivariate or Complex-Valued Signals
Paper and Code
Mar 15, 2017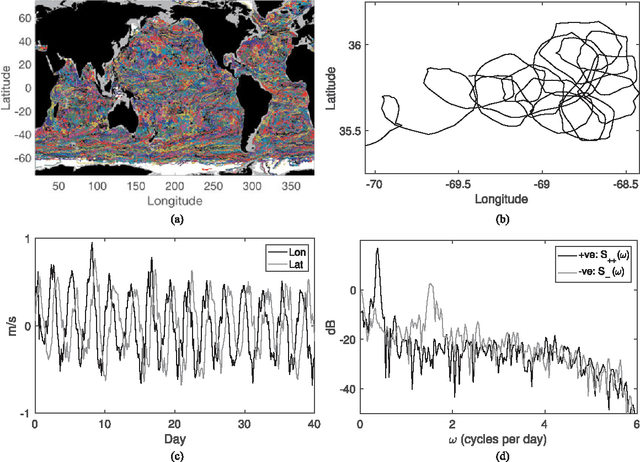

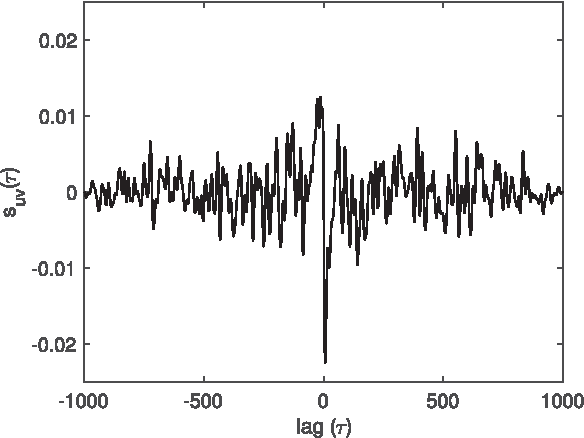
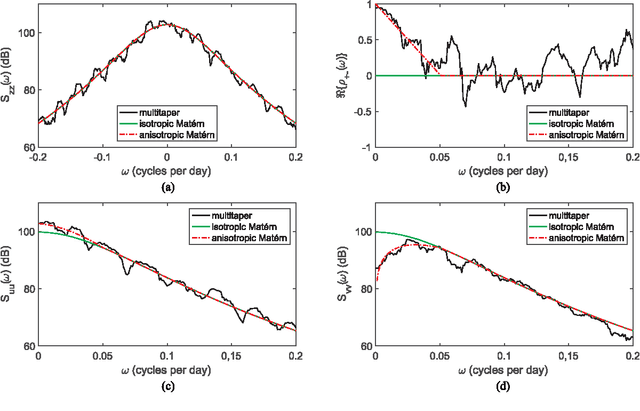
There are three equivalent ways of representing two jointly observed real-valued signals: as a bivariate vector signal, as a single complex-valued signal, or as two analytic signals known as the rotary components. Each representation has unique advantages depending on the system of interest and the application goals. In this paper we provide a joint framework for all three representations in the context of frequency-domain stochastic modeling. This framework allows us to extend many established statistical procedures for bivariate vector time series to complex-valued and rotary representations. These include procedures for parametrically modeling signal coherence, estimating model parameters using the Whittle likelihood, performing semi-parametric modeling, and choosing between classes of nested models using model choice. We also provide a new method of testing for impropriety in complex-valued signals, which tests for noncircular or anisotropic second-order statistical structure when the signal is represented in the complex plane. Finally, we demonstrate the usefulness of our methodology in capturing the anisotropic structure of signals observed from fluid dynamic simulations of turbulence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge