Low-cost Real-world Implementation of the Swing-up Pendulum for Deep Reinforcement Learning Experiments

Deep reinforcement learning (DRL) has had success in virtual and simulated domains, but due to key differences between simulated and real-world environments, DRL-trained policies have had limited success in real-world applications. To assist researchers to bridge the \textit{sim-to-real gap}, in this paper, we describe a low-cost physical inverted pendulum apparatus and software environment for exploring sim-to-real DRL methods. In particular, the design of our apparatus enables detailed examination of the delays that arise in physical systems when sensing, communicating, learning, inferring and actuating. Moreover, we wish to improve access to educational systems, so our apparatus uses readily available materials and parts to reduce cost and logistical barriers. Our design shows how commercial, off-the-shelf electronics and electromechanical and sensor systems, combined with common metal extrusions, dowel and 3D printed couplings provide a pathway for affordable physical DRL apparatus. The physical apparatus is complemented with a simulated environment implemented using a high-fidelity physics engine and OpenAI Gym interface.

Training Directional Locomotion for Quadrupedal Low-Cost Robotic Systems via Deep Reinforcement Learning

In this work we present Deep Reinforcement Learning (DRL) training of directional locomotion for low-cost quadrupedal robots in the real world. In particular, we exploit randomization of heading that the robot must follow to foster exploration of action-state transitions most useful for learning both forward locomotion as well as course adjustments. Changing the heading in episode resets to current yaw plus a random value drawn from a normal distribution yields policies able to follow complex trajectories involving frequent turns in both directions as well as long straight-line stretches. By repeatedly changing the heading, this method keeps the robot moving within the training platform and thus reduces human involvement and need for manual resets during the training. Real world experiments on a custom-built, low-cost quadruped demonstrate the efficacy of our method with the robot successfully navigating all validation tests. When trained with other approaches, the robot only succeeds in forward locomotion test and fails when turning is required.

Macro-action Multi-timescale Dynamic Programming for Energy Management with Phase Change Materials

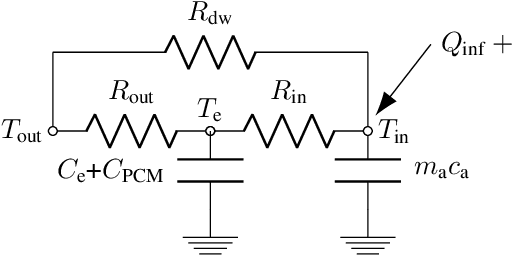
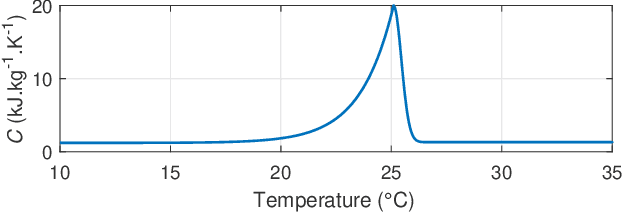
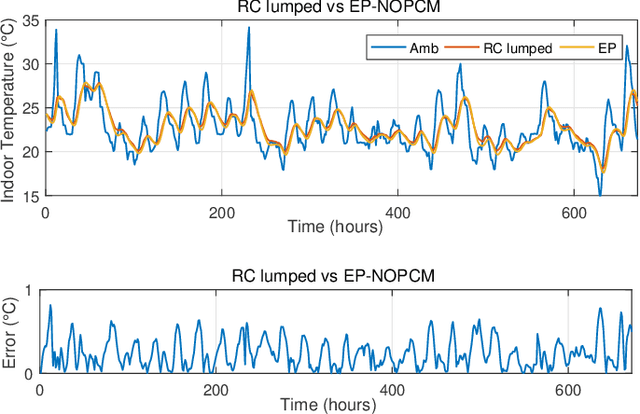
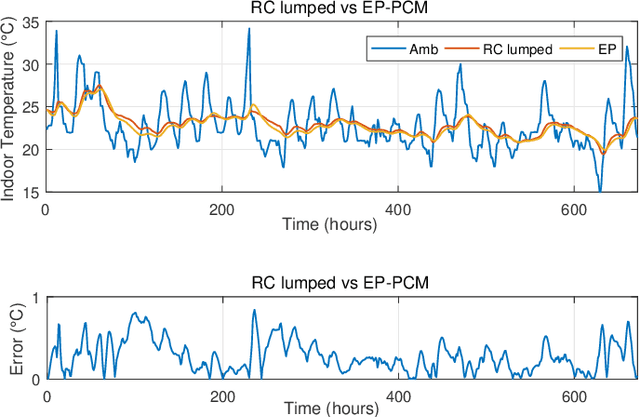
This paper focuses on home energy management systems (HEMS) in buildings that have controllable HVAC systems and use phase change material (PCM) as an energy storage system. In this setting, optimally operating a HVAC system is a challenge, because of the nonlinear and non-convex characteristics of the PCM, which makes the corresponding optimization problem impractical with commonly used methods in HEMS. Instead, we use dynamic programming (DP) to deal with the nonlinear features of PCM. However, DP suffers from the curse of dimensionality. Given this drawback, this paper proposes a novel methodology to reduce the computational burden of the DP algorithm in HEMS optimisation with PCM, while maintaining the quality of the solution. Specifically, the method incorporates approaches from sequential decision making in artificial intelligence, including macro-action and multi-time scale abstractions, coupled with an underlying state-space approximation to reduce state-space and action-space size. The method is demonstrated on an energy management problem for a typical residential building located in Sydney for four seasonal weather conditions. Our results demonstrate that the proposed method performs well with an attractive computational cost. In particular, it has a significant speed-up over directly applying DP to the problem, of up to 12900 times faster.

Automated Planning in Repeated Adversarial Games

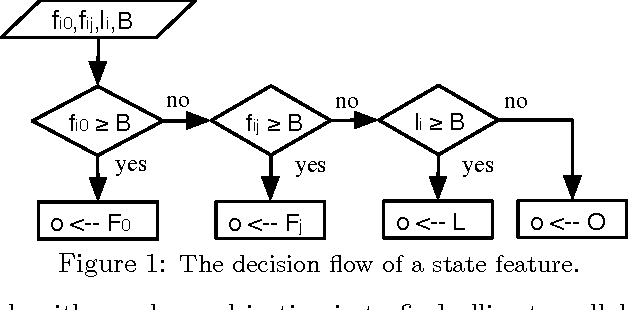
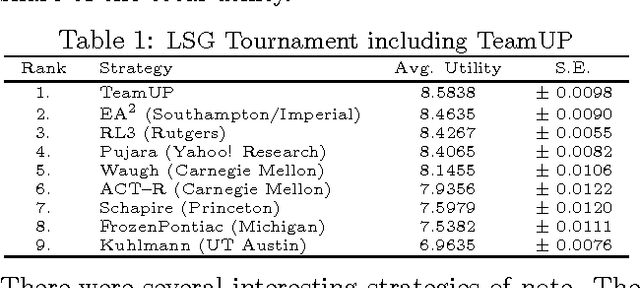
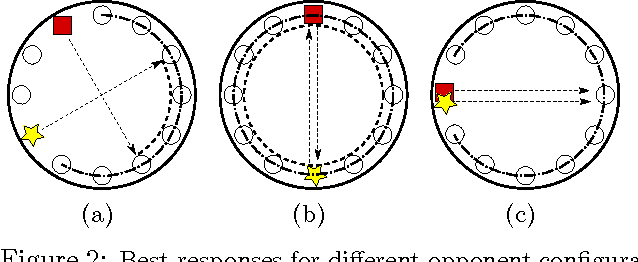
Game theory's prescriptive power typically relies on full rationality and/or self-play interactions. In contrast, this work sets aside these fundamental premises and focuses instead on heterogeneous autonomous interactions between two or more agents. Specifically, we introduce a new and concise representation for repeated adversarial (constant-sum) games that highlight the necessary features that enable an automated planing agent to reason about how to score above the game's Nash equilibrium, when facing heterogeneous adversaries. To this end, we present TeamUP, a model-based RL algorithm designed for learning and planning such an abstraction. In essence, it is somewhat similar to R-max with a cleverly engineered reward shaping that treats exploration as an adversarial optimization problem. In practice, it attempts to find an ally with which to tacitly collude (in more than two-player games) and then collaborates on a joint plan of actions that can consistently score a high utility in adversarial repeated games. We use the inaugural Lemonade Stand Game Tournament to demonstrate the effectiveness of our approach, and find that TeamUP is the best performing agent, demoting the Tournament's actual winning strategy into second place. In our experimental analysis, we show hat our strategy successfully and consistently builds collaborations with many different heterogeneous (and sometimes very sophisticated) adversaries.

Filtered Fictitious Play for Perturbed Observation Potential Games and Decentralised POMDPs

Potential games and decentralised partially observable MDPs (Dec-POMDPs) are two commonly used models of multi-agent interaction, for static optimisation and sequential decisionmaking settings, respectively. In this paper we introduce filtered fictitious play for solving repeated potential games in which each player's observations of others' actions are perturbed by random noise, and use this algorithm to construct an online learning method for solving Dec-POMDPs. Specifically, we prove that noise in observations prevents standard fictitious play from converging to Nash equilibrium in potential games, which also makes fictitious play impractical for solving Dec-POMDPs. To combat this, we derive filtered fictitious play, and provide conditions under which it converges to a Nash equilibrium in potential games with noisy observations. We then use filtered fictitious play to construct a solver for Dec-POMDPs, and demonstrate our new algorithm's performance in a box pushing problem. Our results show that we consistently outperform the state-of-the-art Dec-POMDP solver by an average of 100% across the range of noise in the observation function.