Charles Fisher
Bayesian prognostic covariate adjustment
Dec 24, 2020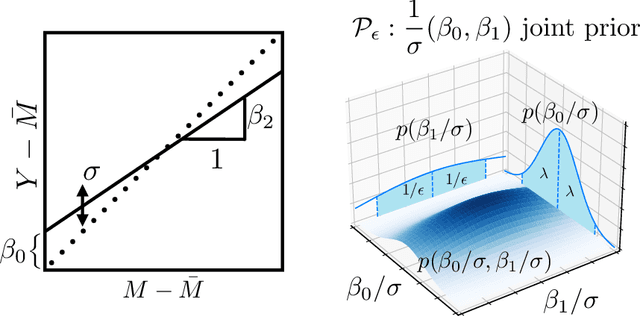
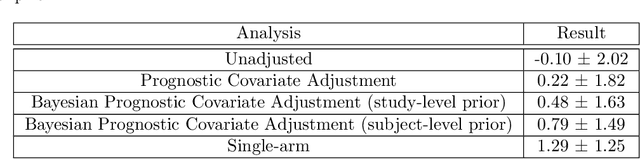
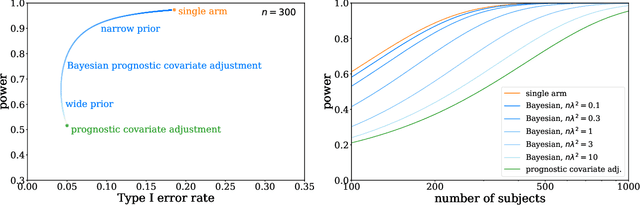
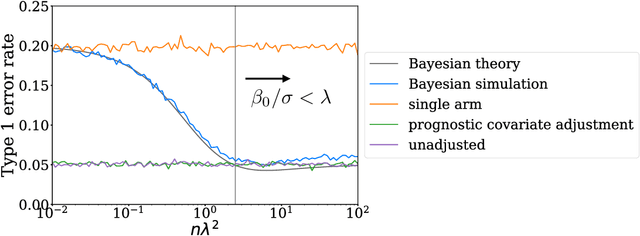
Abstract:Historical data about disease outcomes can be integrated into the analysis of clinical trials in many ways. We build on existing literature that uses prognostic scores from a predictive model to increase the efficiency of treatment effect estimates via covariate adjustment. Here we go further, utilizing a Bayesian framework that combines prognostic covariate adjustment with an empirical prior distribution learned from the predictive performances of the prognostic model on past trials. The Bayesian approach interpolates between prognostic covariate adjustment with strict type I error control when the prior is diffuse, and a single-arm trial when the prior is sharply peaked. This method is shown theoretically to offer a substantial increase in statistical power, while limiting the type I error rate under reasonable conditions. We demonstrate the utility of our method in simulations and with an analysis of a past Alzheimer's disease clinical trial.
Increasing the efficiency of randomized trial estimates via linear adjustment for a prognostic score
Dec 17, 2020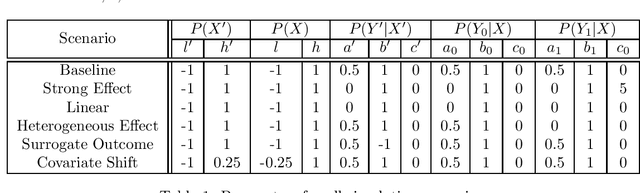
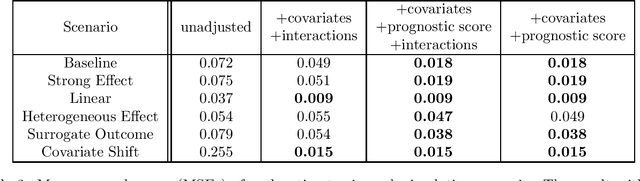
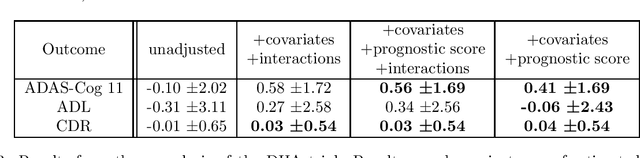

Abstract:Estimating causal effects from randomized experiments is central to clinical research. Reducing the statistical uncertainty in these analyses is an important objective for statisticians. Registries, prior trials, and health records constitute a growing compendium of historical data on patients under standard-of-care conditions that may be exploitable to this end. However, most methods for historical borrowing achieve reductions in variance by sacrificing strict type-I error rate control. Here, we propose a use of historical data that exploits linear covariate adjustment to improve the efficiency of trial analyses without incurring bias. Specifically, we train a prognostic model on the historical data, then estimate the treatment effect using a linear regression while adjusting for the trial subjects' predicted outcomes (their prognostic scores). We prove that, under certain conditions, this prognostic covariate adjustment procedure attains the minimum variance possible among a large class of estimators. When those conditions are not met, prognostic covariate adjustment is still more efficient than raw covariate adjustment and the gain in efficiency is proportional to a measure of the predictive accuracy of the prognostic model. We demonstrate the approach using simulations and a reanalysis of an Alzheimer's Disease clinical trial and observe meaningful reductions in mean-squared error and the estimated variance. Lastly, we provide a simplified formula for asymptotic variance that enables power and sample size calculations that account for the gains from the prognostic model for clinical trial design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge