Selective Reviews of Bandit Problems in AI via a Statistical View

Reinforcement Learning (RL) is a widely researched area in artificial intelligence that focuses on teaching agents decision-making through interactions with their environment. A key subset includes stochastic multi-armed bandit (MAB) and continuum-armed bandit (SCAB) problems, which model sequential decision-making under uncertainty. This review outlines the foundational models and assumptions of bandit problems, explores non-asymptotic theoretical tools like concentration inequalities and minimax regret bounds, and compares frequentist and Bayesian algorithms for managing exploration-exploitation trade-offs. We also extend the discussion to $K$-armed contextual bandits and SCAB, examining their methodologies, regret analyses, and discussing the relation between the SCAB problems and the functional data analysis. Finally, we highlight recent advances and ongoing challenges in the field.

Tight Non-asymptotic Inference via Sub-Gaussian Intrinsic Moment Norm

In non-asymptotic statistical inferences, variance-type parameters of sub-Gaussian distributions play a crucial role. However, direct estimation of these parameters based on the empirical moment generating function (MGF) is infeasible. To this end, we recommend using a sub-Gaussian intrinsic moment norm [Buldygin and Kozachenko (2000), Theorem 1.3] through maximizing a series of normalized moments. Importantly, the recommended norm can not only recover the exponential moment bounds for the corresponding MGFs, but also lead to tighter Hoeffding's sub-Gaussian concentration inequalities. In practice, {\color{black} we propose an intuitive way of checking sub-Gaussian data with a finite sample size by the sub-Gaussian plot}. Intrinsic moment norm can be robustly estimated via a simple plug-in approach. Our theoretical results are applied to non-asymptotic analysis, including the multi-armed bandit.

Distribution Estimation of Contaminated Data via DNN-based MoM-GANs

This paper studies the distribution estimation of contaminated data by the MoM-GAN method, which combines generative adversarial net (GAN) and median-of-mean (MoM) estimation. We use a deep neural network (DNN) with a ReLU activation function to model the generator and discriminator of the GAN. Theoretically, we derive a non-asymptotic error bound for the DNN-based MoM-GAN estimator measured by integral probability metrics with the $b$-smoothness H\"{o}lder class. The error bound decreases essentially as $n^{-b/p}\vee n^{-1/2}$, where $n$ and $p$ are the sample size and the dimension of input data. We give an algorithm for the MoM-GAN method and implement it through two real applications. The numerical results show that the MoM-GAN outperforms other competitive methods when dealing with contaminated data.

Inference and FDR Control for Simulated Ising Models in High-dimension

This paper studies the consistency and statistical inference of simulated Ising models in the high dimensional background. Our estimators are based on the Markov chain Monte Carlo maximum likelihood estimation (MCMC-MLE) method penalized by the Elastic-net. Under mild conditions that ensure a specific convergence rate of MCMC method, the $\ell_{1}$ consistency of Elastic-net-penalized MCMC-MLE is proved. We further propose a decorrelated score test based on the decorrelated score function and prove the asymptotic normality of the score function without the influence of many nuisance parameters under the assumption that accelerates the convergence of the MCMC method. The one-step estimator for a single parameter of interest is purposed by linearizing the decorrelated score function to solve its root, as well as its normality and confidence interval for the true value, therefore, be established. Finally, we use different algorithms to control the false discovery rate (FDR) via traditional p-values and novel e-values.

Non-Asymptotic Guarantees for Robust Statistical Learning under $(1+\varepsilon)$-th Moment Assumption

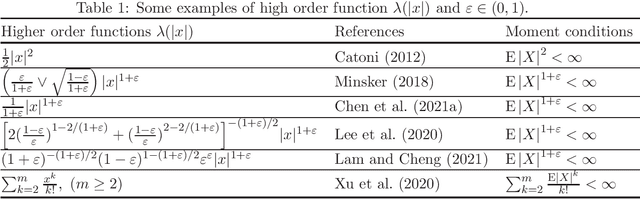
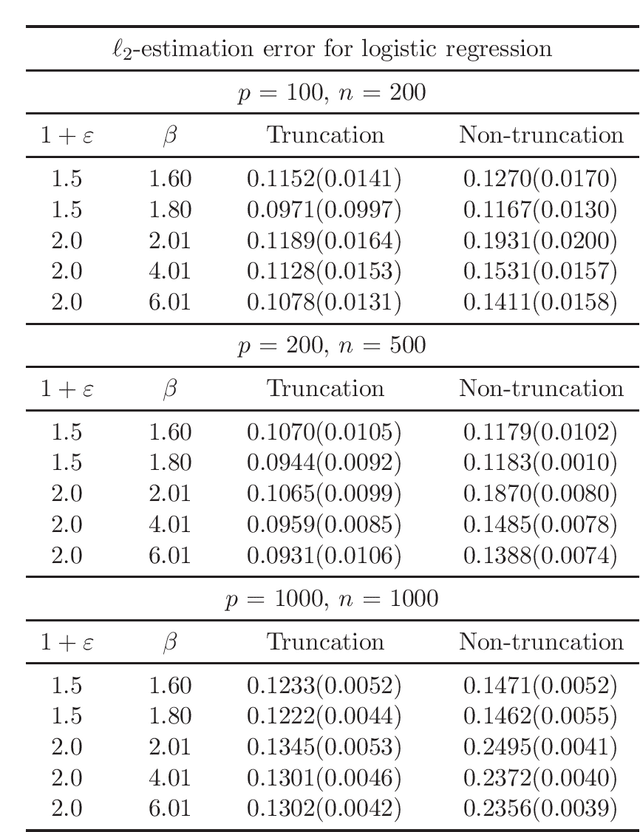
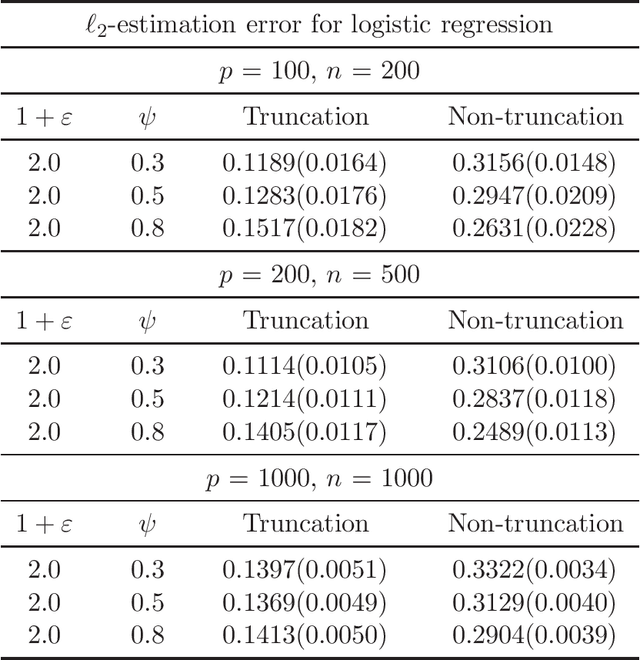
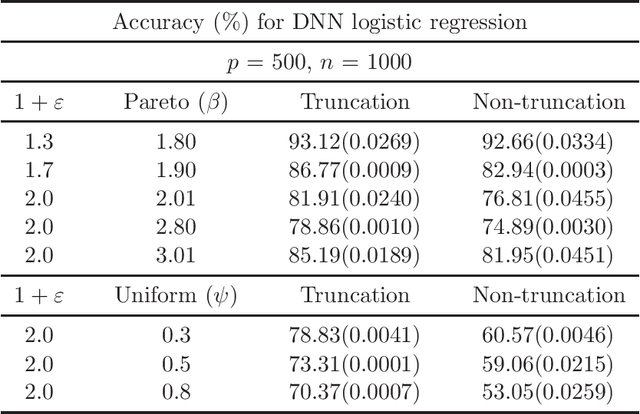
There has been a surge of interest in developing robust estimators for models with heavy-tailed data in statistics and machine learning. This paper proposes a log-truncated M-estimator for a large family of statistical regressions and establishes its excess risk bound under the condition that the data have $(1+\varepsilon)$-th moment with $\varepsilon \in (0,1]$. With an additional assumption on the associated risk function, we obtain an $\ell_2$-error bound for the estimation. Our theorems are applied to establish robust M-estimators for concrete regressions. Besides convex regressions such as quantile regression and generalized linear models, many non-convex regressions can also be fit into our theorems, we focus on robust deep neural network regressions, which can be solved by the stochastic gradient descent algorithms. Simulations and real data analysis demonstrate the superiority of log-truncated estimations over standard estimations.

Adaptive Fusion Affinity Graph with Noise-free Online Low-rank Representation for Natural Image Segmentation

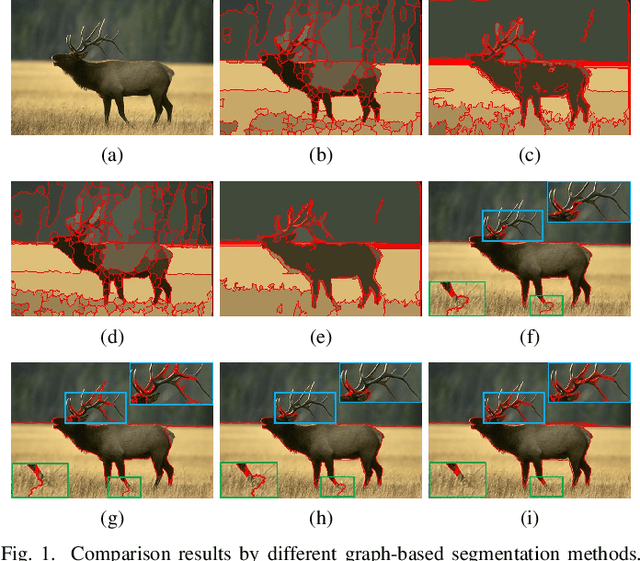
Affinity graph-based segmentation methods have become a major trend in computer vision. The performance of these methods relies on the constructed affinity graph, with particular emphasis on the neighborhood topology and pairwise affinities among superpixels. Due to the advantages of assimilating different graphs, a multi-scale fusion graph has a better performance than a single graph with single-scale. However, these methods ignore the noise from images which influences the accuracy of pairwise similarities. Multi-scale combinatorial grouping and graph fusion also generate a higher computational complexity. In this paper, we propose an adaptive fusion affinity graph (AFA-graph) with noise-free low-rank representation in an online manner for natural image segmentation. An input image is first over-segmented into superpixels at different scales and then filtered by the proposed improved kernel density estimation method. Moreover, we select global nodes of these superpixels on the basis of their subspace-preserving presentation, which reveals the feature distribution of superpixels exactly. To reduce time complexity while improving performance, a sparse representation of global nodes based on noise-free online low-rank representation is used to obtain a global graph at each scale. The global graph is finally used to update a local graph which is built upon all superpixels at each scale. Experimental results on the BSD300, BSD500, MSRC, SBD, and PASCAL VOC show the effectiveness of AFA-graph in comparison with state-of-the-art approaches.

Directional FDR Control for Sub-Gaussian Sparse GLMs

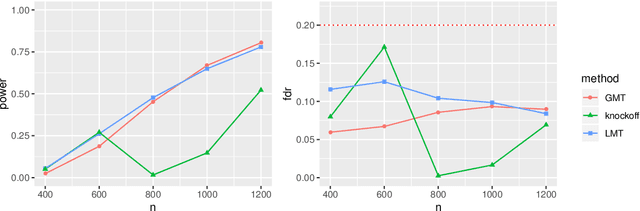
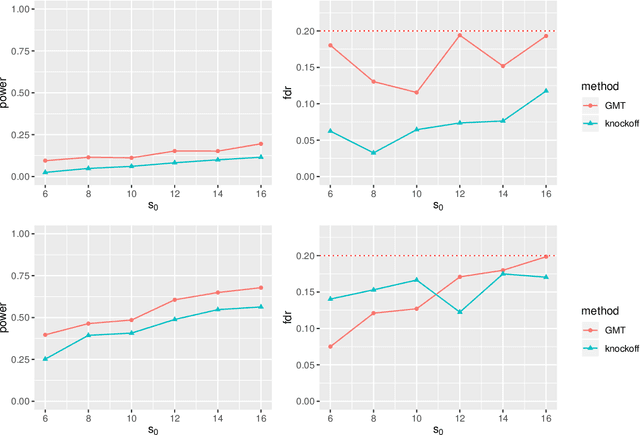
High-dimensional sparse generalized linear models (GLMs) have emerged in the setting that the number of samples and the dimension of variables are large, and even the dimension of variables grows faster than the number of samples. False discovery rate (FDR) control aims to identify some small number of statistically significantly nonzero results after getting the sparse penalized estimation of GLMs. Using the CLIME method for precision matrix estimations, we construct the debiased-Lasso estimator and prove the asymptotical normality by minimax-rate oracle inequalities for sparse GLMs. In practice, it is often needed to accurately judge each regression coefficient's positivity and negativity, which determines whether the predictor variable is positively or negatively related to the response variable conditionally on the rest variables. Using the debiased estimator, we establish multiple testing procedures. Under mild conditions, we show that the proposed debiased statistics can asymptotically control the directional (sign) FDR and directional false discovery variables at a pre-specified significance level. Moreover, it can be shown that our multiple testing procedure can approximately achieve a statistical power of 1. We also extend our methods to the two-sample problems and propose the two-sample test statistics. Under suitable conditions, we can asymptotically achieve directional FDR control and directional FDV control at the specified significance level for two-sample problems. Some numerical simulations have successfully verified the FDR control effects of our proposed testing procedures, which sometimes outperforms the classical knockoff method.

Sharper Sub-Weibull Concentrations: Non-asymptotic Bai-Yin Theorem

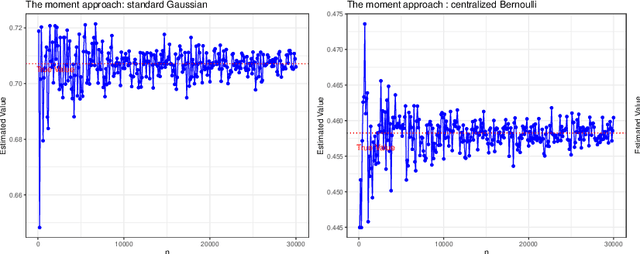
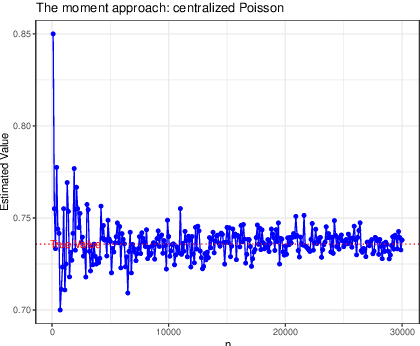
Arising in high-dimensional probability, non-asymptotic concentration inequalities play an essential role in the finite-sample theory of machine learning and high-dimensional statistics. In this article, we obtain a sharper and constants-specified concentration inequality for the summation of independent sub-Weibull random variables, which leads to a mixture of two tails: sub-Gaussian for small deviations and sub-Weibull for large deviations (from mean). These bounds improve existing bounds with sharper constants. In the application of random matrices, we derive non-asymptotic versions of Bai-Yin's theorem for sub-Weibull entries and it extends the previous result in terms of sub-Gaussian entries. In the application of negative binomial regressions, we gives the $\ell_2$-error of the estimated coefficients when covariate vector $X$ is sub-Weibull distributed with sparse structures, which is a new result for negative binomial regressions.

A Unified Light Framework for Real-time Fault Detection of Freight Train Images

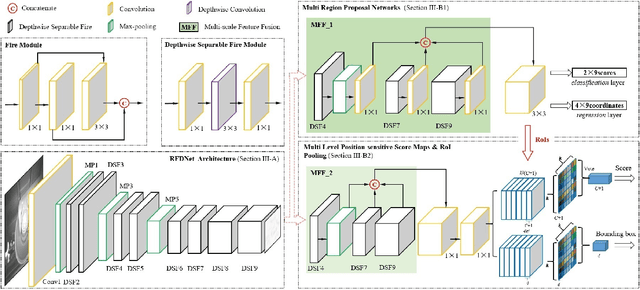
Real-time fault detection for freight trains plays a vital role in guaranteeing the security and optimal operation of railway transportation under stringent resource requirements. Despite the promising results for deep learning based approaches, the performance of these fault detectors on freight train images, are far from satisfactory in both accuracy and efficiency. This paper proposes a unified light framework to improve detection accuracy while supporting a real-time operation with a low resource requirement. We firstly design a novel lightweight backbone (RFDNet) to improve the accuracy and reduce computational cost. Then, we propose a multi region proposal network using multi-scale feature maps generated from RFDNet to improve the detection performance. Finally, we present multi level position-sensitive score maps and region of interest pooling to further improve accuracy with few redundant computations. Extensive experimental results on public benchmark datasets suggest that our RFDNet can significantly improve the performance of baseline network with higher accuracy and efficiency. Experiments on six fault datasets show that our method is capable of real-time detection at over 38 frames per second and achieves competitive accuracy and lower computation than the state-of-the-art detectors.

Concentration Inequalities for Statistical Inference

This paper gives a review of concentration inequalities which are widely employed in analyzes of mathematical statistics in a wide range of settings, from distribution free to distribution dependent, from sub-Gaussian to sub-exponential, sub-Gamma, and sub-Weibull random variables, and from the mean to the maximum concentration. This review provides results in these settings with some fresh new results. Given the increasing popularity of high dimensional data and inference, results in the context of high-dimensional linear and Poisson regressions are also provided. We aim to illustrate the concentration inequalities with known constants and to improve existing bounds with sharper constants.