Learned Off-aperture Encoding for Wide Field-of-view RGBD Imaging

End-to-end (E2E) designed imaging systems integrate coded optical designs with decoding algorithms to enhance imaging fidelity for diverse visual tasks. However, existing E2E designs encounter significant challenges in maintaining high image fidelity at wide fields of view, due to high computational complexity, as well as difficulties in modeling off-axis wave propagation while accounting for off-axis aberrations. In particular, the common approach of placing the encoding element into the aperture or pupil plane results in only a global control of the wavefront. To overcome these limitations, this work explores an additional design choice by positioning a DOE off-aperture, enabling a spatial unmixing of the degrees of freedom and providing local control over the wavefront over the image plane. Our approach further leverages hybrid refractive-diffractive optical systems by linking differentiable ray and wave optics modeling, thereby optimizing depth imaging quality and demonstrating system versatility. Experimental results reveal that the off-aperture DOE enhances the imaging quality by over 5 dB in PSNR at a FoV of approximately $45^\circ$ when paired with a simple thin lens, outperforming traditional on-aperture systems. Furthermore, we successfully recover color and depth information at nearly $28^\circ$ FoV using off-aperture DOE configurations with compound optics. Physical prototypes for both applications validate the effectiveness and versatility of the proposed method.

Characterization of Efficient Influence Function for Off-Policy Evaluation Under Optimal Policies

Off-policy evaluation (OPE) provides a powerful framework for estimating the value of a counterfactual policy using observational data, without the need for additional experimentation. Despite recent progress in robust and efficient OPE across various settings, rigorous efficiency analysis of OPE under an estimated optimal policy remains limited. In this paper, we establish a concise characterization of the efficient influence function (EIF) for the value function under optimal policy within canonical Markov decision process models. Specifically, we provide the sufficient conditions for the existence of the EIF and characterize its expression. We also give the conditions under which the EIF does not exist.

Selective Reviews of Bandit Problems in AI via a Statistical View

Reinforcement Learning (RL) is a widely researched area in artificial intelligence that focuses on teaching agents decision-making through interactions with their environment. A key subset includes stochastic multi-armed bandit (MAB) and continuum-armed bandit (SCAB) problems, which model sequential decision-making under uncertainty. This review outlines the foundational models and assumptions of bandit problems, explores non-asymptotic theoretical tools like concentration inequalities and minimax regret bounds, and compares frequentist and Bayesian algorithms for managing exploration-exploitation trade-offs. We also extend the discussion to $K$-armed contextual bandits and SCAB, examining their methodologies, regret analyses, and discussing the relation between the SCAB problems and the functional data analysis. Finally, we highlight recent advances and ongoing challenges in the field.

Zero-Inflated Bandits

Many real applications of bandits have sparse non-zero rewards, leading to slow learning rates. A careful distribution modeling that utilizes problem-specific structures is known as critical to estimation efficiency in the statistics literature, yet is under-explored in bandits. To fill the gap, we initiate the study of zero-inflated bandits, where the reward is modeled as a classic semi-parametric distribution called zero-inflated distribution. We carefully design Upper Confidence Bound (UCB) and Thompson Sampling (TS) algorithms for this specific structure. Our algorithms are suitable for a very general class of reward distributions, operating under tail assumptions that are considerably less stringent than the typical sub-Gaussian requirements. Theoretically, we derive the regret bounds for both the UCB and TS algorithms for multi-armed bandit, showing that they can achieve rate-optimal regret when the reward distribution is sub-Gaussian. The superior empirical performance of the proposed methods is shown via extensive numerical studies.

Tight Non-asymptotic Inference via Sub-Gaussian Intrinsic Moment Norm

In non-asymptotic statistical inferences, variance-type parameters of sub-Gaussian distributions play a crucial role. However, direct estimation of these parameters based on the empirical moment generating function (MGF) is infeasible. To this end, we recommend using a sub-Gaussian intrinsic moment norm [Buldygin and Kozachenko (2000), Theorem 1.3] through maximizing a series of normalized moments. Importantly, the recommended norm can not only recover the exponential moment bounds for the corresponding MGFs, but also lead to tighter Hoeffding's sub-Gaussian concentration inequalities. In practice, {\color{black} we propose an intuitive way of checking sub-Gaussian data with a finite sample size by the sub-Gaussian plot}. Intrinsic moment norm can be robustly estimated via a simple plug-in approach. Our theoretical results are applied to non-asymptotic analysis, including the multi-armed bandit.

Multiplier Bootstrap-based Exploration

Despite the great interest in the bandit problem, designing efficient algorithms for complex models remains challenging, as there is typically no analytical way to quantify uncertainty. In this paper, we propose Multiplier Bootstrap-based Exploration (MBE), a novel exploration strategy that is applicable to any reward model amenable to weighted loss minimization. We prove both instance-dependent and instance-independent rate-optimal regret bounds for MBE in sub-Gaussian multi-armed bandits. With extensive simulation and real data experiments, we show the generality and adaptivity of MBE.

Inference and FDR Control for Simulated Ising Models in High-dimension

This paper studies the consistency and statistical inference of simulated Ising models in the high dimensional background. Our estimators are based on the Markov chain Monte Carlo maximum likelihood estimation (MCMC-MLE) method penalized by the Elastic-net. Under mild conditions that ensure a specific convergence rate of MCMC method, the $\ell_{1}$ consistency of Elastic-net-penalized MCMC-MLE is proved. We further propose a decorrelated score test based on the decorrelated score function and prove the asymptotic normality of the score function without the influence of many nuisance parameters under the assumption that accelerates the convergence of the MCMC method. The one-step estimator for a single parameter of interest is purposed by linearizing the decorrelated score function to solve its root, as well as its normality and confidence interval for the true value, therefore, be established. Finally, we use different algorithms to control the false discovery rate (FDR) via traditional p-values and novel e-values.

Asymptotic in a class of network models with sub-Gamma perturbations

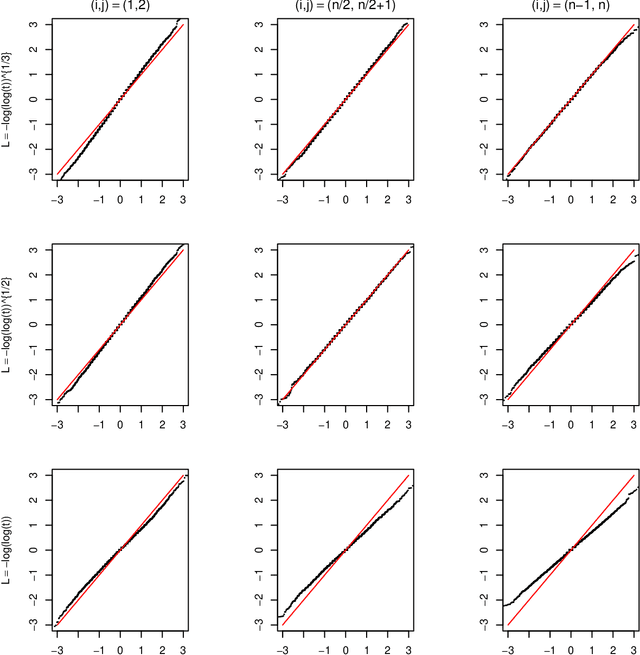
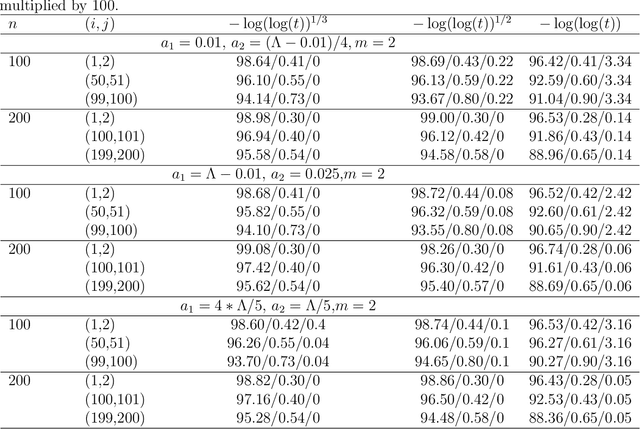
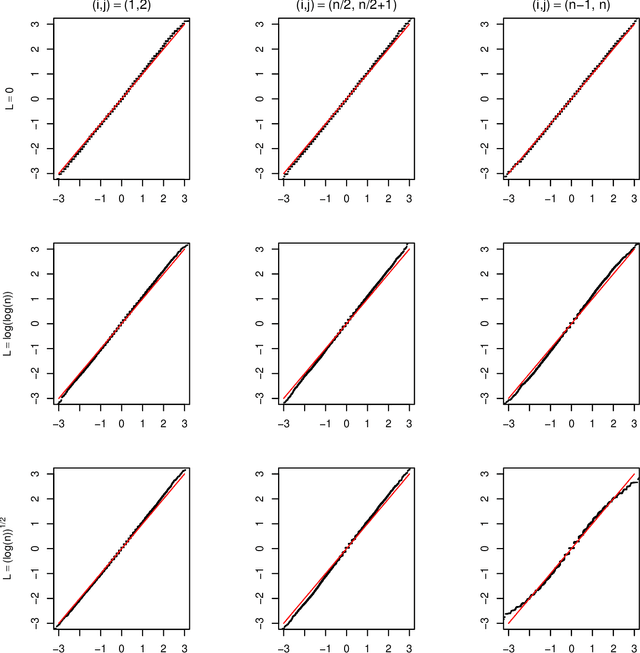
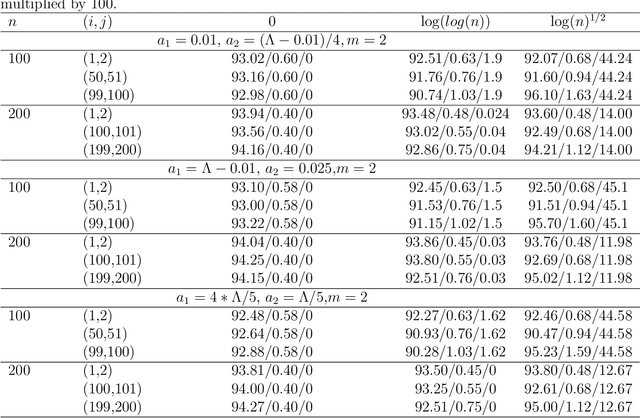
For the differential privacy under the sub-Gamma noise, we derive the asymptotic properties of a class of network models with binary values with a general link function. In this paper, we release the degree sequences of the binary networks under a general noisy mechanism with the discrete Laplace mechanism as a special case. We establish the asymptotic result including both consistency and asymptotically normality of the parameter estimator when the number of parameters goes to infinity in a class of network models. Simulations and a real data example are provided to illustrate asymptotic results.

Heterogeneous Overdispersed Count Data Regressions via Double Penalized Estimations

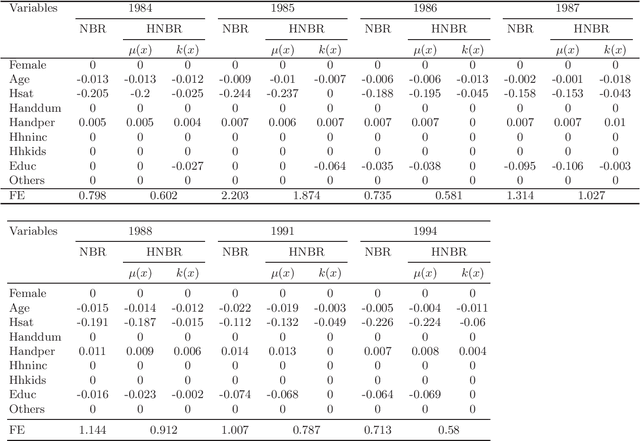
This paper studies the non-asymptotic merits of the double $\ell_1$-regularized for heterogeneous overdispersed count data via negative binomial regressions. Under the restricted eigenvalue conditions, we prove the oracle inequalities for Lasso estimators of two partial regression coefficients for the first time, using concentration inequalities of empirical processes. Furthermore, derived from the oracle inequalities, the consistency and convergence rate for the estimators are the theoretical guarantees for further statistical inference. Finally, both simulations and a real data analysis demonstrate that the new methods are effective.

Sharper Sub-Weibull Concentrations: Non-asymptotic Bai-Yin Theorem

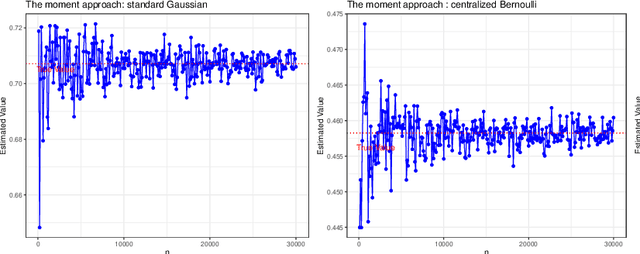
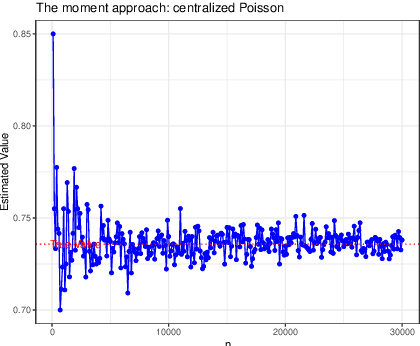
Arising in high-dimensional probability, non-asymptotic concentration inequalities play an essential role in the finite-sample theory of machine learning and high-dimensional statistics. In this article, we obtain a sharper and constants-specified concentration inequality for the summation of independent sub-Weibull random variables, which leads to a mixture of two tails: sub-Gaussian for small deviations and sub-Weibull for large deviations (from mean). These bounds improve existing bounds with sharper constants. In the application of random matrices, we derive non-asymptotic versions of Bai-Yin's theorem for sub-Weibull entries and it extends the previous result in terms of sub-Gaussian entries. In the application of negative binomial regressions, we gives the $\ell_2$-error of the estimated coefficients when covariate vector $X$ is sub-Weibull distributed with sparse structures, which is a new result for negative binomial regressions.