Sharper Sub-Weibull Concentrations: Non-asymptotic Bai-Yin Theorem

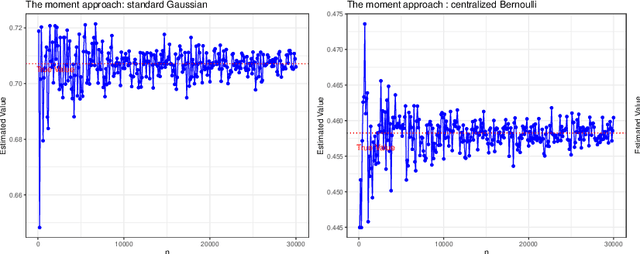
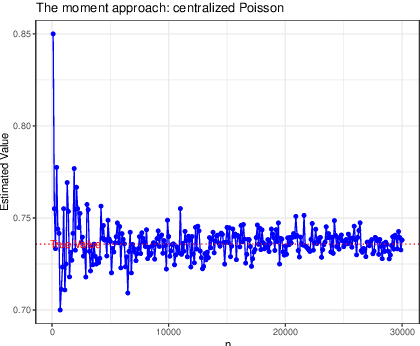
Arising in high-dimensional probability, non-asymptotic concentration inequalities play an essential role in the finite-sample theory of machine learning and high-dimensional statistics. In this article, we obtain a sharper and constants-specified concentration inequality for the summation of independent sub-Weibull random variables, which leads to a mixture of two tails: sub-Gaussian for small deviations and sub-Weibull for large deviations (from mean). These bounds improve existing bounds with sharper constants. In the application of random matrices, we derive non-asymptotic versions of Bai-Yin's theorem for sub-Weibull entries and it extends the previous result in terms of sub-Gaussian entries. In the application of negative binomial regressions, we gives the $\ell_2$-error of the estimated coefficients when covariate vector $X$ is sub-Weibull distributed with sparse structures, which is a new result for negative binomial regressions.