Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Shaomin Li
Heterogeneous Overdispersed Count Data Regressions via Double Penalized Estimations
Oct 07, 2021Figures and Tables:

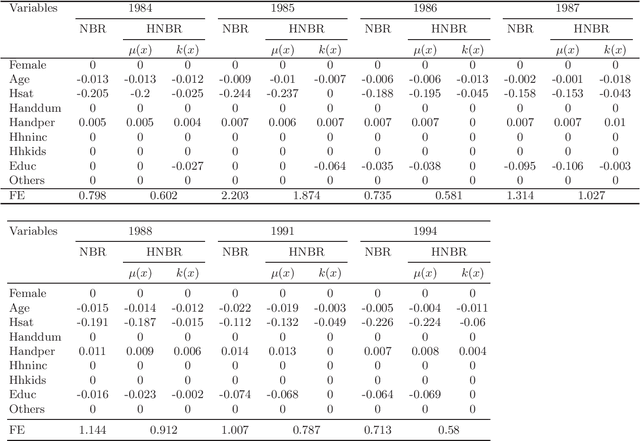



Abstract:This paper studies the non-asymptotic merits of the double $\ell_1$-regularized for heterogeneous overdispersed count data via negative binomial regressions. Under the restricted eigenvalue conditions, we prove the oracle inequalities for Lasso estimators of two partial regression coefficients for the first time, using concentration inequalities of empirical processes. Furthermore, derived from the oracle inequalities, the consistency and convergence rate for the estimators are the theoretical guarantees for further statistical inference. Finally, both simulations and a real data analysis demonstrate that the new methods are effective.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge