Homography matrix based trajectory planning method for robot uncalibrated visual servoing

In view of the classical visual servoing trajectory planning method which only considers the camera trajectory, this paper proposes one homography matrix based trajectory planning method for robot uncalibrated visual servoing. Taking the robot-end-effector frame as one generic case, eigenvalue decomposition is utilized to calculate the infinite homography matrix of the robot-end-effector trajectory, and then the image feature-point trajectories corresponding to the camera rotation is obtained, while the image feature-point trajectories corresponding to the camera translation is obtained by the homography matrix. According to the additional image corresponding to the robot-end-effector rotation, the relationship between the robot-end-effector rotation and the variation of the image feature-points is obtained, and then the expression of the image trajectories corresponding to the optimal robot-end-effector trajectories (the rotation trajectory of the minimum geodesic and the linear translation trajectory) are obtained. Finally, the optimal image trajectories of the uncalibrated visual servoing controller is modified to track the image trajectories. Simulation experiments show that, compared with the classical IBUVS method, the proposed trajectory planning method can obtain the shortest path of any frame and complete the robot visual servoing task with large initial pose deviation.

Inference and FDR Control for Simulated Ising Models in High-dimension

This paper studies the consistency and statistical inference of simulated Ising models in the high dimensional background. Our estimators are based on the Markov chain Monte Carlo maximum likelihood estimation (MCMC-MLE) method penalized by the Elastic-net. Under mild conditions that ensure a specific convergence rate of MCMC method, the $\ell_{1}$ consistency of Elastic-net-penalized MCMC-MLE is proved. We further propose a decorrelated score test based on the decorrelated score function and prove the asymptotic normality of the score function without the influence of many nuisance parameters under the assumption that accelerates the convergence of the MCMC method. The one-step estimator for a single parameter of interest is purposed by linearizing the decorrelated score function to solve its root, as well as its normality and confidence interval for the true value, therefore, be established. Finally, we use different algorithms to control the false discovery rate (FDR) via traditional p-values and novel e-values.

Asymptotic in a class of network models with sub-Gamma perturbations

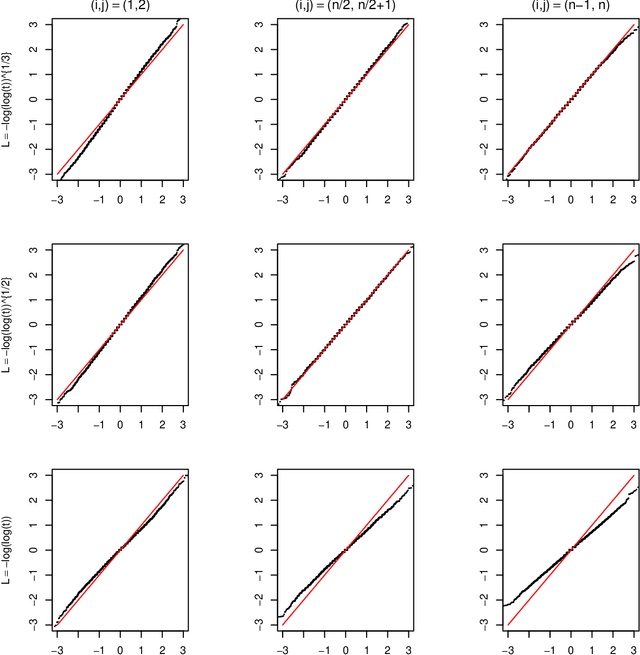
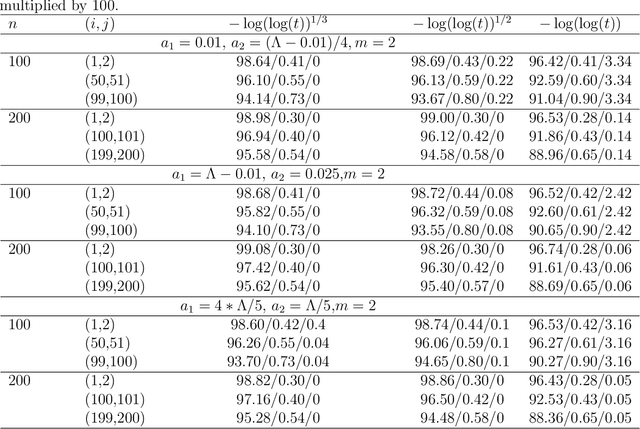
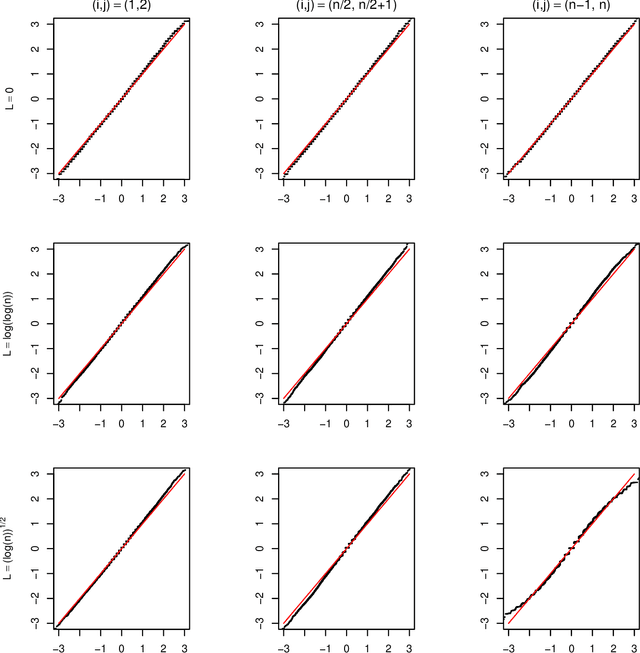
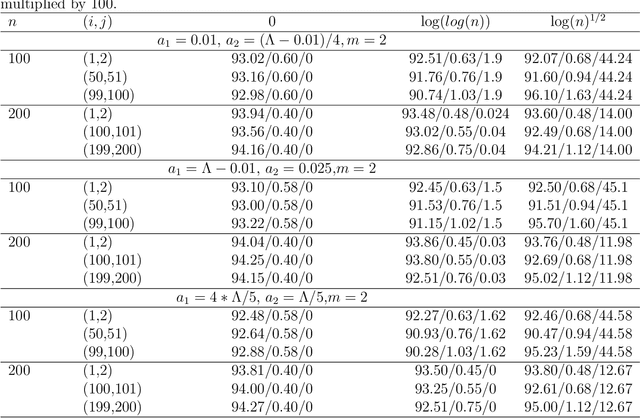
For the differential privacy under the sub-Gamma noise, we derive the asymptotic properties of a class of network models with binary values with a general link function. In this paper, we release the degree sequences of the binary networks under a general noisy mechanism with the discrete Laplace mechanism as a special case. We establish the asymptotic result including both consistency and asymptotically normality of the parameter estimator when the number of parameters goes to infinity in a class of network models. Simulations and a real data example are provided to illustrate asymptotic results.

Heterogeneous Overdispersed Count Data Regressions via Double Penalized Estimations

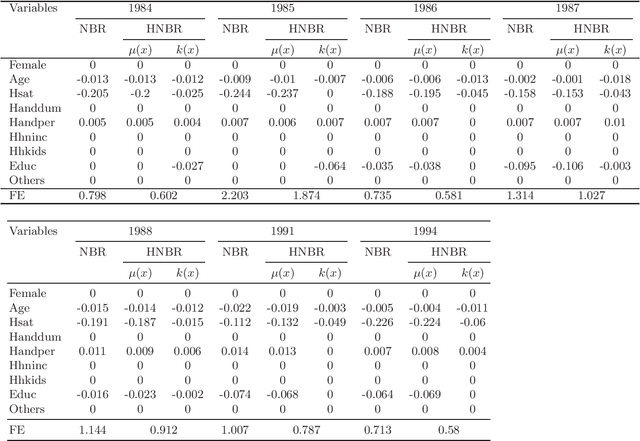
This paper studies the non-asymptotic merits of the double $\ell_1$-regularized for heterogeneous overdispersed count data via negative binomial regressions. Under the restricted eigenvalue conditions, we prove the oracle inequalities for Lasso estimators of two partial regression coefficients for the first time, using concentration inequalities of empirical processes. Furthermore, derived from the oracle inequalities, the consistency and convergence rate for the estimators are the theoretical guarantees for further statistical inference. Finally, both simulations and a real data analysis demonstrate that the new methods are effective.

Non-asymptotic Optimal Prediction Error for RKHS-based Partially Functional Linear Models

Under the framework of reproducing kernel Hilbert space (RKHS), we consider the penalized least-squares of the partially functional linear models (PFLM), whose predictor contains both functional and traditional multivariate part, and the multivariate part allows a divergent number of parameters. From the non-asymptotic point of view, we focus on the rate-optimal upper and lower bounds of the prediction error. An exact upper bound for the excess prediction risk is shown in a non-asymptotic form under a more general assumption known as the effective dimension to the model, by which we also show the prediction consistency when the number of multivariate covariates $p$ slightly increases with the sample size $n$. Our new finding implies a trade-off between the number of non-functional predictors and the effective dimension of the kernel principal components to ensure the prediction consistency in the increasing-dimensional setting. The analysis in our proof hinges on the spectral condition of the sandwich operator of the covariance operator and the reproducing kernel, and on the concentration inequalities for the random elements in Hilbert space. Finally, we derive the non-asymptotic minimax lower bound under the regularity assumption of Kullback-Leibler divergence of the models.