Song Xi Chen
Concentration Inequalities for Statistical Inference
Nov 04, 2020Abstract:This paper gives a review of concentration inequalities which are widely employed in analyzes of mathematical statistics in a wide range of settings, from distribution free to distribution dependent, from sub-Gaussian to sub-exponential, sub-Gamma, and sub-Weibull random variables, and from the mean to the maximum concentration. This review provides results in these settings with some fresh new results. Given the increasing popularity of high dimensional data and inference, results in the context of high-dimensional linear and Poisson regressions are also provided. We aim to illustrate the concentration inequalities with known constants and to improve existing bounds with sharper constants.
Matrix Completion under Low-Rank Missing Mechanism
Dec 19, 2018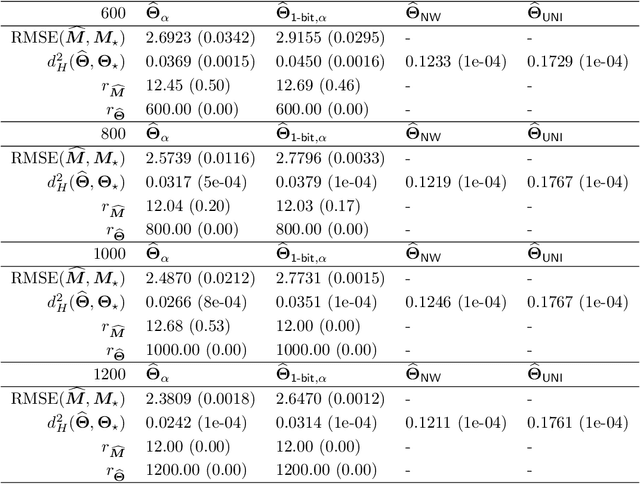
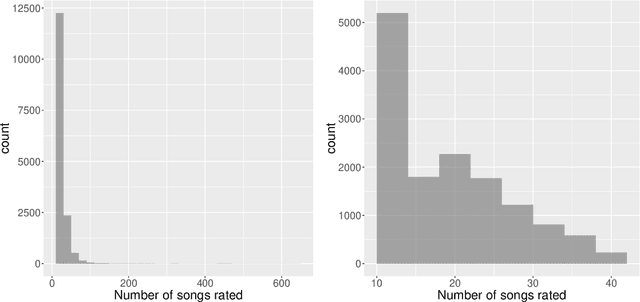
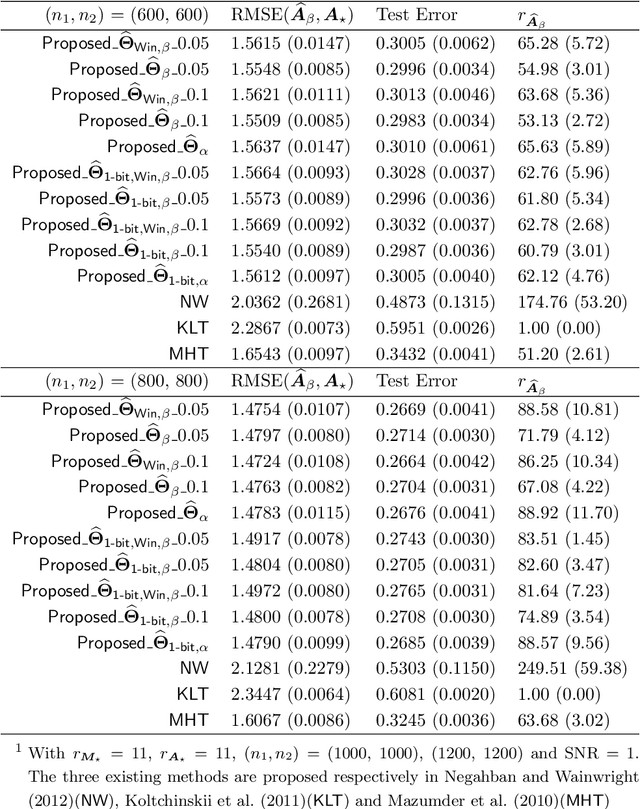
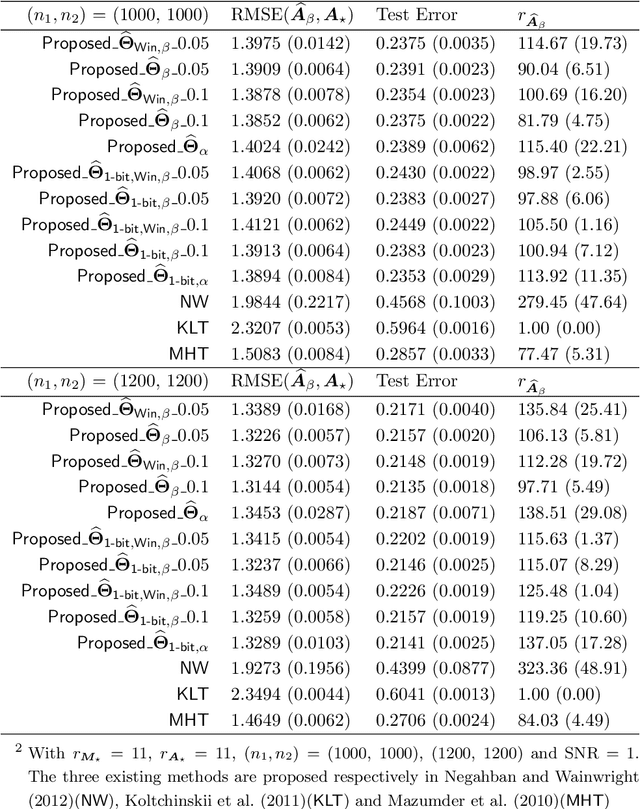
Abstract:This paper investigates the problem of matrix completion from corrupted data, when a low-rank missing mechanism is considered. The better recovery of missing mechanism often helps completing the unobserved entries of the high-dimensional target matrix. Instead of the widely used uniform risk function, we weight the observations by inverse probabilities of observation, which are estimated through a specifically designed high-dimensional estimation procedure. Asymptotic convergence rates of the proposed estimators for both the observation probabilities and the target matrix are studied. The empirical performance of the proposed methodology is illustrated via both numerical experiments and a real data application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge