Matrix Completion under Low-Rank Missing Mechanism
Paper and Code
Dec 19, 2018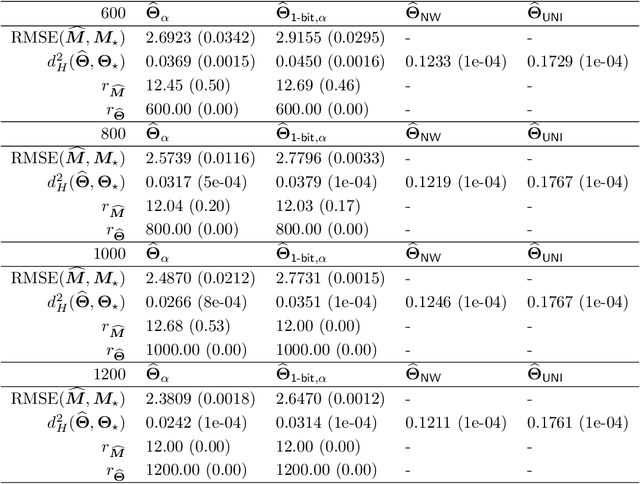
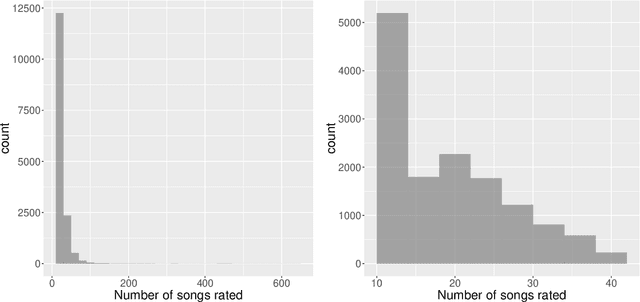
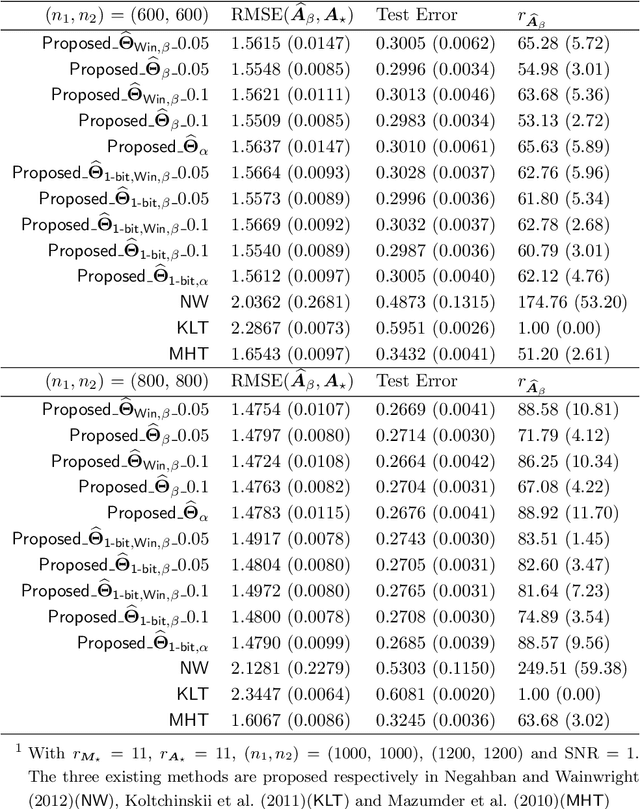
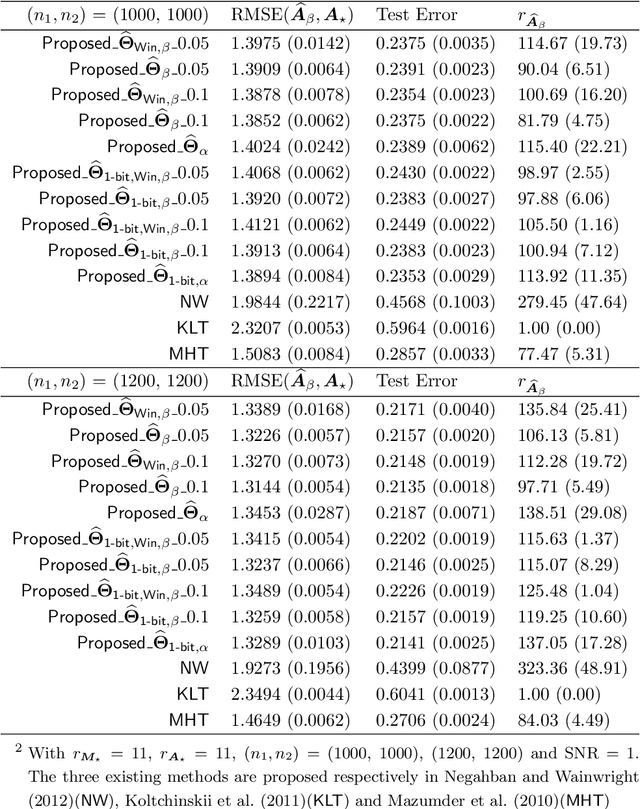
This paper investigates the problem of matrix completion from corrupted data, when a low-rank missing mechanism is considered. The better recovery of missing mechanism often helps completing the unobserved entries of the high-dimensional target matrix. Instead of the widely used uniform risk function, we weight the observations by inverse probabilities of observation, which are estimated through a specifically designed high-dimensional estimation procedure. Asymptotic convergence rates of the proposed estimators for both the observation probabilities and the target matrix are studied. The empirical performance of the proposed methodology is illustrated via both numerical experiments and a real data application.
* 31 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge