Matrix Completion via Residual Spectral Matching

Noisy matrix completion has attracted significant attention due to its applications in recommendation systems, signal processing and image restoration. Most existing works rely on (weighted) least squares methods under various low-rank constraints. However, minimizing the sum of squared residuals is not always efficient, as it may ignore the potential structural information in the residuals.In this study, we propose a novel residual spectral matching criterion that incorporates not only the numerical but also locational information of residuals. This criterion is the first in noisy matrix completion to adopt the perspective of low-rank perturbation of random matrices and exploit the spectral properties of sparse random matrices. We derive optimal statistical properties by analyzing the spectral properties of sparse random matrices and bounding the effects of low-rank perturbations and partial observations. Additionally, we propose algorithms that efficiently approximate solutions by constructing easily computable pseudo-gradients. The iterative process of the proposed algorithms ensures convergence at a rate consistent with the optimal statistical error bound. Our method and algorithms demonstrate improved numerical performance in both simulated and real data examples, particularly in environments with high noise levels.

Policy Evaluation for Temporal and/or Spatial Dependent Experiments in Ride-sourcing Platforms

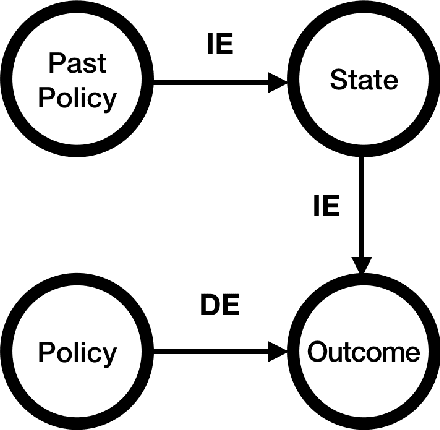
Policy evaluation based on A/B testing has attracted considerable interest in digital marketing, but such evaluation in ride-sourcing platforms (e.g., Uber and Didi) is not well studied primarily due to the complex structure of their temporal and/or spatial dependent experiments. Motivated by policy evaluation in ride-sourcing platforms, the aim of this paper is to establish causal relationship between platform's policies and outcomes of interest under a switchback design. We propose a novel potential outcome framework based on a temporal varying coefficient decision process (VCDP) model to capture the dynamic treatment effects in temporal dependent experiments. We further characterize the average treatment effect by decomposing it as the sum of direct effect (DE) and indirect effect (IE). We develop estimation and inference procedures for both DE and IE. Furthermore, we propose a spatio-temporal VCDP to deal with spatiotemporal dependent experiments. For both VCDP models, we establish the statistical properties (e.g., weak convergence and asymptotic power) of our estimation and inference procedures. We conduct extensive simulations to investigate the finite-sample performance of the proposed estimation and inference procedures. We examine how our VCDP models can help improve policy evaluation for various dispatching and dispositioning policies in Didi.

Non-Asymptotic Guarantees for Robust Statistical Learning under $(1+\varepsilon)$-th Moment Assumption

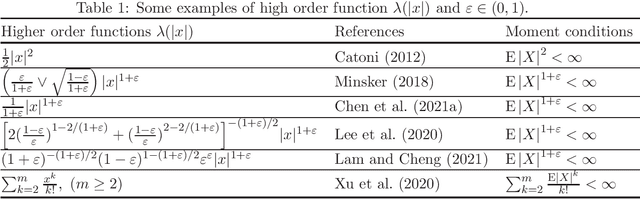
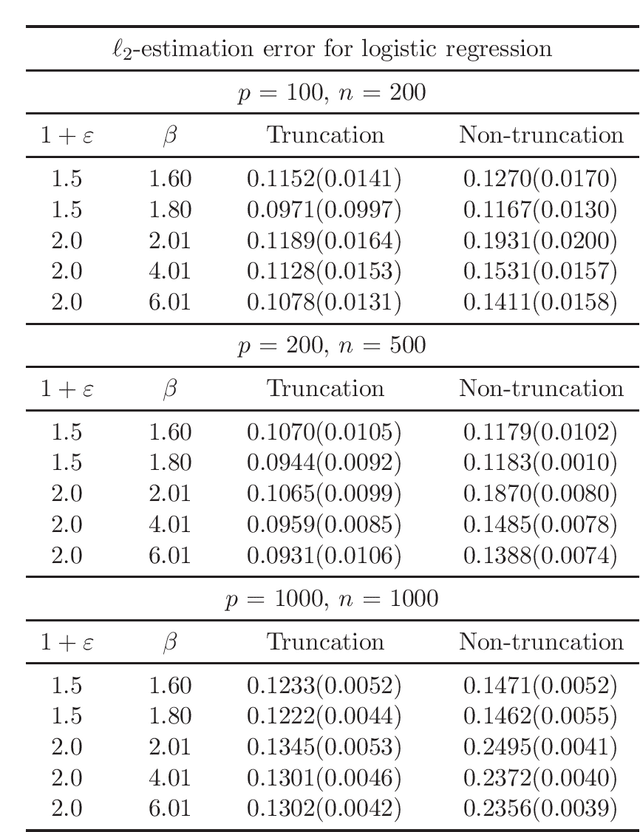
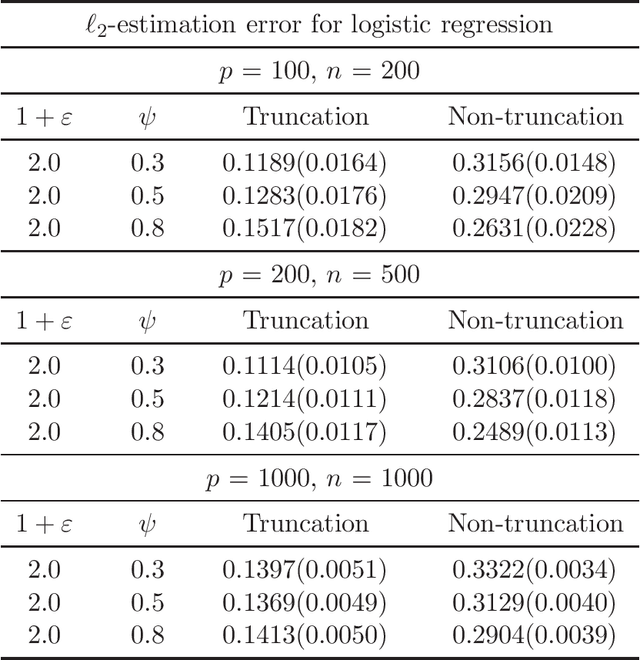
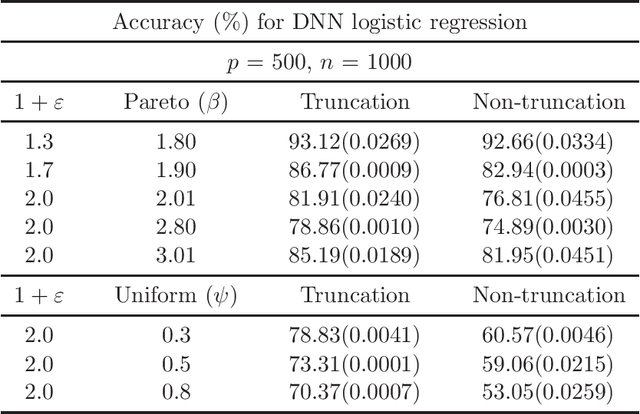
There has been a surge of interest in developing robust estimators for models with heavy-tailed data in statistics and machine learning. This paper proposes a log-truncated M-estimator for a large family of statistical regressions and establishes its excess risk bound under the condition that the data have $(1+\varepsilon)$-th moment with $\varepsilon \in (0,1]$. With an additional assumption on the associated risk function, we obtain an $\ell_2$-error bound for the estimation. Our theorems are applied to establish robust M-estimators for concrete regressions. Besides convex regressions such as quantile regression and generalized linear models, many non-convex regressions can also be fit into our theorems, we focus on robust deep neural network regressions, which can be solved by the stochastic gradient descent algorithms. Simulations and real data analysis demonstrate the superiority of log-truncated estimations over standard estimations.