Qiuran Yao
Distribution Estimation of Contaminated Data via DNN-based MoM-GANs
Dec 28, 2022Abstract:This paper studies the distribution estimation of contaminated data by the MoM-GAN method, which combines generative adversarial net (GAN) and median-of-mean (MoM) estimation. We use a deep neural network (DNN) with a ReLU activation function to model the generator and discriminator of the GAN. Theoretically, we derive a non-asymptotic error bound for the DNN-based MoM-GAN estimator measured by integral probability metrics with the $b$-smoothness H\"{o}lder class. The error bound decreases essentially as $n^{-b/p}\vee n^{-1/2}$, where $n$ and $p$ are the sample size and the dimension of input data. We give an algorithm for the MoM-GAN method and implement it through two real applications. The numerical results show that the MoM-GAN outperforms other competitive methods when dealing with contaminated data.
Distribution estimation and change-point detection for time series via DNN-based GANs
Nov 26, 2022Abstract:The generative adversarial networks (GANs) have recently been applied to estimating the distribution of independent and identically distributed data, and got excellent performances. In this paper, we use the blocking technique to demonstrate the effectiveness of GANs for estimating the distribution of stationary time series. Theoretically, we obtain a non-asymptotic error bound for the Deep Neural Network (DNN)-based GANs estimator for the stationary distribution of the time series. Based on our theoretical analysis, we put forward an algorithm for detecting the change-point in time series. We simulate in our first experiment a stationary time series by the multivariate autoregressive model to test our GAN estimator, while the second experiment is to use our proposed algorithm to detect the change-point in a time series sequence. Both perform very well. The third experiment is to use our GAN estimator to learn the distribution of a real financial time series data, which is not stationary, we can see from the experiment results that our estimator cannot match the distribution of the time series very well but give the right changing tendency.
Non-Asymptotic Guarantees for Robust Statistical Learning under $(1+\varepsilon)$-th Moment Assumption
Jan 10, 2022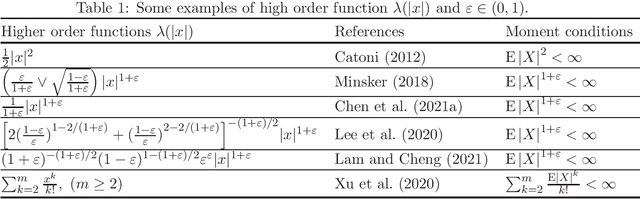
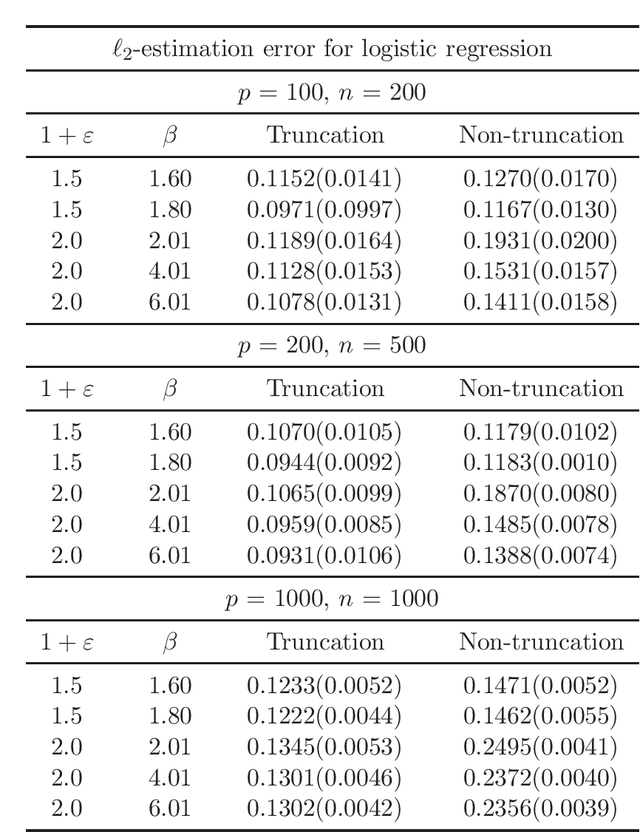
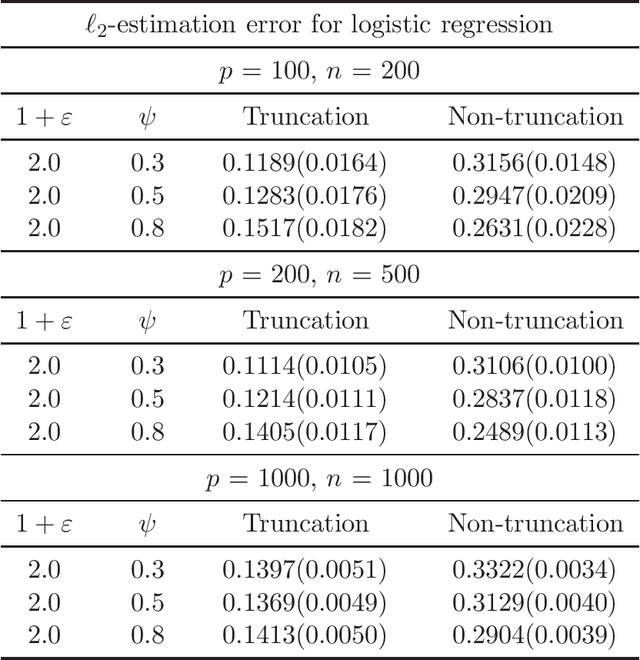
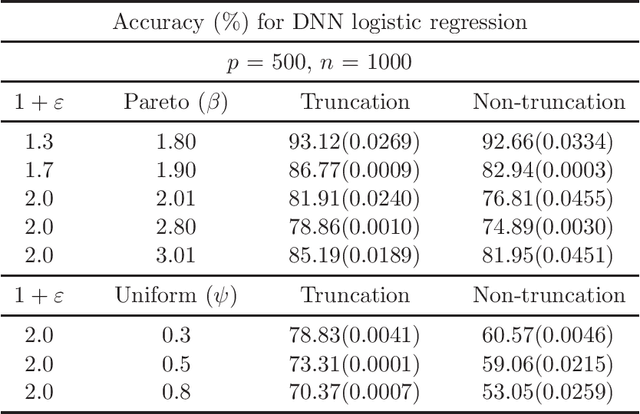
Abstract:There has been a surge of interest in developing robust estimators for models with heavy-tailed data in statistics and machine learning. This paper proposes a log-truncated M-estimator for a large family of statistical regressions and establishes its excess risk bound under the condition that the data have $(1+\varepsilon)$-th moment with $\varepsilon \in (0,1]$. With an additional assumption on the associated risk function, we obtain an $\ell_2$-error bound for the estimation. Our theorems are applied to establish robust M-estimators for concrete regressions. Besides convex regressions such as quantile regression and generalized linear models, many non-convex regressions can also be fit into our theorems, we focus on robust deep neural network regressions, which can be solved by the stochastic gradient descent algorithms. Simulations and real data analysis demonstrate the superiority of log-truncated estimations over standard estimations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge