The Lasso under Heteroscedasticity
Paper and Code
Nov 03, 2010
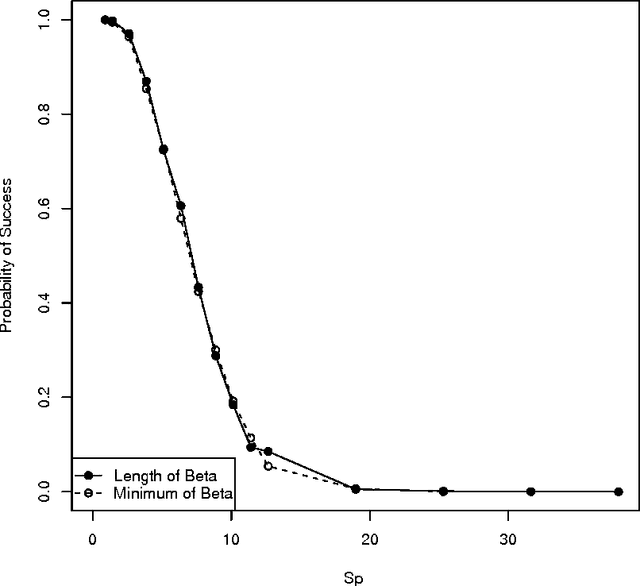

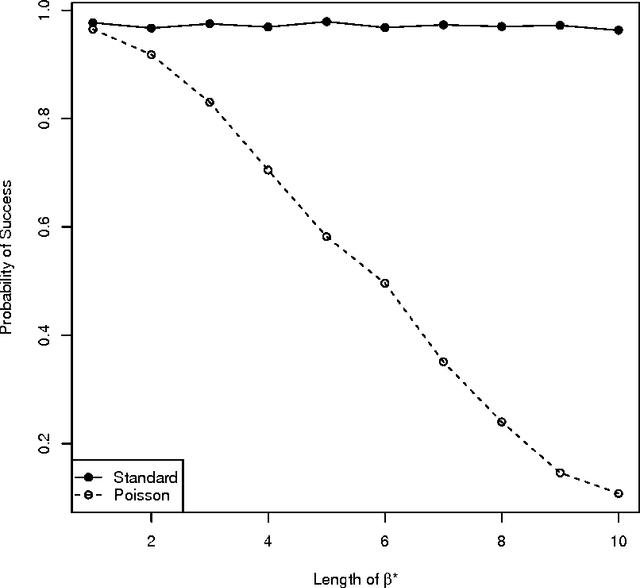
The performance of the Lasso is well understood under the assumptions of the standard linear model with homoscedastic noise. However, in several applications, the standard model does not describe the important features of the data. This paper examines how the Lasso performs on a non-standard model that is motivated by medical imaging applications. In these applications, the variance of the noise scales linearly with the expectation of the observation. Like all heteroscedastic models, the noise terms in this Poisson-like model are \textit{not} independent of the design matrix. More specifically, this paper studies the sign consistency of the Lasso under a sparse Poisson-like model. In addition to studying sufficient conditions for the sign consistency of the Lasso estimate, this paper also gives necessary conditions for sign consistency. Both sets of conditions are comparable to results for the homoscedastic model, showing that when a measure of the signal to noise ratio is large, the Lasso performs well on both Poisson-like data and homoscedastic data. Simulations reveal that the Lasso performs equally well in terms of model selection performance on both Poisson-like data and homoscedastic data (with properly scaled noise variance), across a range of parameterizations. Taken as a whole, these results suggest that the Lasso is robust to the Poisson-like heteroscedastic noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge