Formulas for Counting the Sizes of Markov Equivalence Classes of Directed Acyclic Graphs
Paper and Code
Oct 23, 2016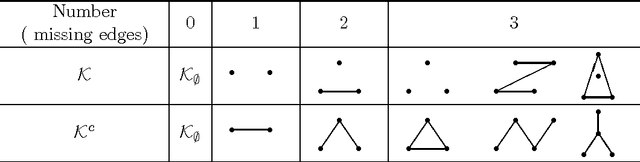
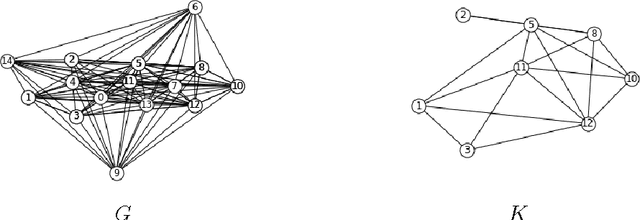
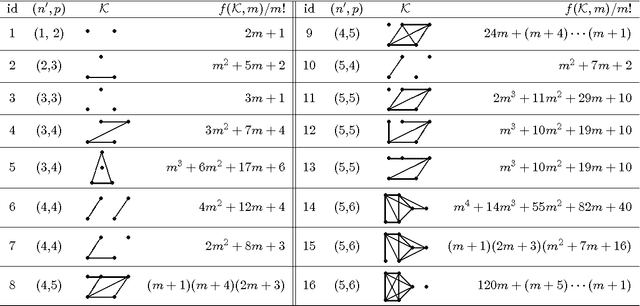
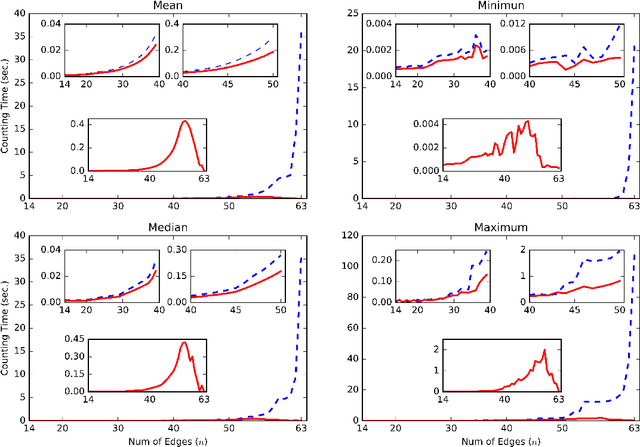
The sizes of Markov equivalence classes of directed acyclic graphs play important roles in measuring the uncertainty and complexity in causal learning. A Markov equivalence class can be represented by an essential graph and its undirected subgraphs determine the size of the class. In this paper, we develop a method to derive the formulas for counting the sizes of Markov equivalence classes. We first introduce a new concept of core graph. The size of a Markov equivalence class of interest is a polynomial of the number of vertices given its core graph. Then, we discuss the recursive and explicit formula of the polynomial, and provide an algorithm to derive the size formula via symbolic computation for any given core graph. The proposed size formula derivation sheds light on the relationships between the size of a Markov equivalence class and its representation graph, and makes size counting efficient, even when the essential graphs contain non-sparse undirected subgraphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge