Training Large Language Models to be Better Rule Followers

Large language models (LLMs) have shown impressive performance across a wide range of tasks. However, they often exhibit unexpected failures in seemingly straightforward tasks, suggesting a reliance on case-based reasoning rather than rule-based reasoning. While the vast training corpus of LLMs contains numerous textual "rules", current training methods fail to leverage these rules effectively. Crucially, the relationships between these "rules" and their corresponding "instances" are not explicitly modeled. As a result, while LLMs can often recall rules with ease, they fail to apply these rules strictly and consistently in relevant reasoning scenarios. In this paper, we investigate the rule-following capabilities of LLMs and propose Meta Rule-Following Fine-Tuning (Meta-RFFT) to enhance the cross-task transferability of rule-following abilities. We first construct a dataset of 88 tasks requiring following rules, encompassing diverse reasoning domains. We demonstrate through extensive experiments that models trained on large-scale rule-following tasks are better rule followers, outperforming the baselines in both downstream fine-tuning and few-shot prompting scenarios. This highlights the cross-task transferability of models with the aid of Meta-RFFT. Furthermore, we examine the influence of factors such as dataset size, rule formulation, and in-context learning.

RedStar: Does Scaling Long-CoT Data Unlock Better Slow-Reasoning Systems?

Can scaling transform reasoning? In this work, we explore the untapped potential of scaling Long Chain-of-Thought (Long-CoT) data to 1000k samples, pioneering the development of a slow-thinking model, RedStar. Through extensive experiments with various LLMs and different sizes, we uncover the ingredients for specialization and scale for Long-CoT training. Surprisingly, even smaller models show significant performance gains with limited data, revealing the sample efficiency of Long-CoT and the critical role of sample difficulty in the learning process. Our findings demonstrate that Long-CoT reasoning can be effectively triggered with just a few thousand examples, while larger models achieve unparalleled improvements. We also introduce reinforcement learning (RL)-scale training as a promising direction for advancing slow-thinking systems. RedStar shines across domains: on the MATH-Hard benchmark, RedStar-code-math boosts performance from 66.2\% to 81.6\%, and on the USA Math Olympiad (AIME), it solves 46.7\% of problems using only 21k mixed-code-math datasets. In multimodal tasks like GeoQA and MathVista-GEO, RedStar-Geo achieves competitive results with minimal Long-CoT data, outperforming other slow-thinking systems like QvQ-Preview. Compared to QwQ, RedStar strikes the perfect balance between reasoning and generalizability. Our work highlights that, with careful tuning, scaling Long-CoT can unlock extraordinary reasoning capabilities-even with limited dataset and set a new standard for slow-thinking models across diverse challenges. Our data and models are released at https://huggingface.co/RedStar-Reasoning.

Number Cookbook: Number Understanding of Language Models and How to Improve It

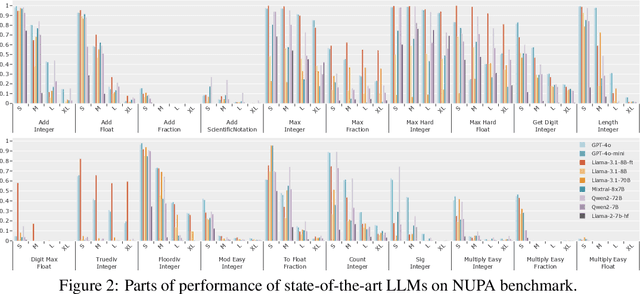
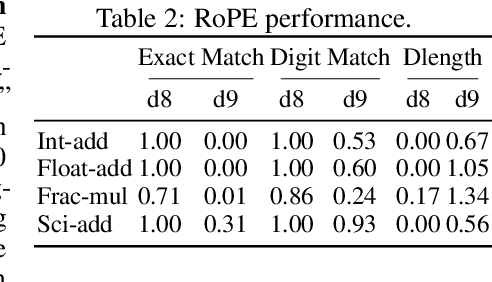
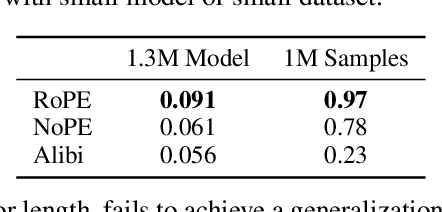
Large language models (LLMs) can solve an increasing number of complex reasoning tasks while making surprising mistakes in basic numerical understanding and processing (such as 9.11 > 9.9). The latter ability is essential for tackling complex arithmetic and mathematical problems and serves as a foundation for most reasoning tasks, but previous work paid little attention to it or only discussed several restricted tasks (like integer addition). In this paper, we comprehensively investigate the numerical understanding and processing ability (NUPA) of LLMs. Firstly, we introduce a benchmark covering four common numerical representations and 17 distinct numerical tasks in four major categories, resulting in 41 meaningful combinations in total. These tasks are derived from primary and secondary education curricula, encompassing nearly all everyday numerical understanding and processing scenarios, and the rules of these tasks are very simple and clear. Through the benchmark, we find that current LLMs fail frequently in many of the tasks. To study the problem, we train small models with existing and potential techniques for enhancing NUPA (such as special tokenizers, PEs, and number formats), comprehensively evaluating their effectiveness using our testbed. We also finetune practical-scale LLMs on our proposed NUPA tasks and find that 1) naive finetuning can improve NUPA a lot on many but not all tasks, and 2) surprisingly, techniques designed to enhance NUPA prove ineffective for finetuning pretrained models. We further explore the impact of chain-of-thought techniques on NUPA. Our work takes a preliminary step towards understanding and improving NUPA of LLMs. Our benchmark and code are released at https://github.com/GraphPKU/number_cookbook.

On the Completeness of Invariant Geometric Deep Learning Models

Invariant models, one important class of geometric deep learning models, are capable of generating meaningful geometric representations by leveraging informative geometric features. These models are characterized by their simplicity, good experimental results and computational efficiency. However, their theoretical expressive power still remains unclear, restricting a deeper understanding of the potential of such models. In this work, we concentrate on characterizing the theoretical expressiveness of invariant models. We first rigorously bound the expressiveness of the most classical invariant model, Vanilla DisGNN (message passing neural networks incorporating distance), restricting its unidentifiable cases to be only those highly symmetric geometric graphs. To break these corner cases' symmetry, we introduce a simple yet E(3)-complete invariant design by nesting Vanilla DisGNN, named GeoNGNN. Leveraging GeoNGNN as a theoretical tool, we for the first time prove the E(3)-completeness of three well-established geometric models: DimeNet, GemNet and SphereNet. Our results fill the gap in the theoretical power of invariant models, contributing to a rigorous and comprehensive understanding of their capabilities. Experimentally, GeoNGNN exhibits good inductive bias in capturing local environments, and achieves competitive results w.r.t. complicated models relying on high-order invariant/equivariant representations while exhibiting significantly faster computational speed.