Is Distance Matrix Enough for Geometric Deep Learning?

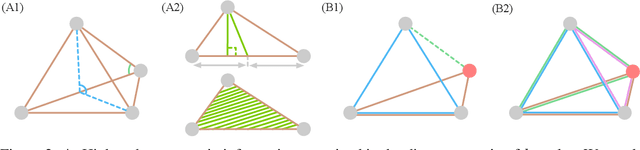
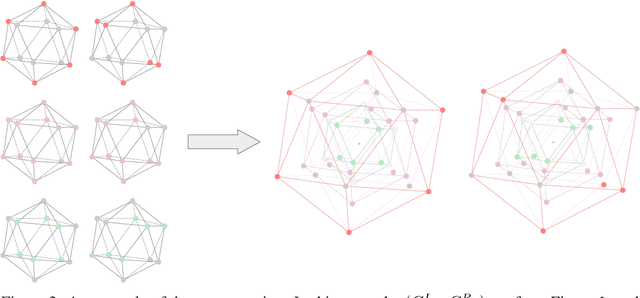
Graph Neural Networks (GNNs) are often used for tasks involving the geometry of a given graph, such as molecular dynamics simulation. While the distance matrix of a graph contains the complete geometric structure information, whether GNNs can learn this geometry solely from the distance matrix has yet to be studied. In this work, we first demonstrate that Message Passing Neural Networks (MPNNs) are insufficient for learning the geometry of a graph from its distance matrix by constructing families of geometric graphs which cannot be distinguished by MPNNs. We then propose $k$-DisGNNs, which can effectively exploit the rich geometry contained in the distance matrix. We demonstrate the high expressive power of our models and prove that some existing well-designed geometric models can be unified by $k$-DisGNNs as special cases. Most importantly, we establish a connection between geometric deep learning and traditional graph representation learning, showing that those highly expressive GNN models originally designed for graph structure learning can also be applied to geometric deep learning problems with impressive performance, and that existing complex, equivariant models are not the only solution. Experimental results verify our theory.