What Are Good Positional Encodings for Directed Graphs?
Paper and Code
Jul 30, 2024
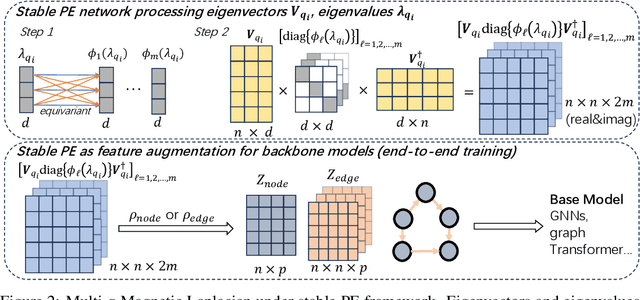


Positional encodings (PE) for graphs are essential in constructing powerful and expressive graph neural networks and graph transformers as they effectively capture relative spatial relations between nodes. While PEs for undirected graphs have been extensively studied, those for directed graphs remain largely unexplored, despite the fundamental role of directed graphs in representing entities with strong logical dependencies, such as those in program analysis and circuit designs. This work studies the design of PEs for directed graphs that are expressive to represent desired directed spatial relations. We first propose walk profile, a generalization of walk counting sequence to directed graphs. We identify limitations in existing PE methods, including symmetrized Laplacian PE, Singular Value Decomposition PE, and Magnetic Laplacian PE, in their ability to express walk profiles. To address these limitations, we propose the Multi-q Magnetic Laplacian PE, which extends Magnetic Laplacian PE with multiple potential factors. This simple variant turns out to be capable of provably expressing walk profiles. Furthermore, we generalize previous basis-invariant and stable networks to handle complex-domain PEs decomposed from Magnetic Laplacians. Our numerical experiments demonstrate the effectiveness of Multi-q Magnetic Laplacian PE with a stable neural architecture, outperforming previous PE methods (with stable networks) on predicting directed distances/walk profiles, sorting network satisfiability, and on general circuit benchmarks. Our code is available at https://github.com/Graph-COM/Multi-q-Maglap.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge