Fair Wasserstein Coresets

Recent technological advancements have given rise to the ability of collecting vast amounts of data, that often exceed the capacity of commonly used machine learning algorithms. Approaches such as coresets and synthetic data distillation have emerged as frameworks to generate a smaller, yet representative, set of samples for downstream training. As machine learning is increasingly applied to decision-making processes, it becomes imperative for modelers to consider and address biases in the data concerning subgroups defined by factors like race, gender, or other sensitive attributes. Current approaches focus on creating fair synthetic representative samples by optimizing local properties relative to the original samples. These methods, however, are not guaranteed to positively affect the performance or fairness of downstream learning processes. In this work, we present Fair Wasserstein Coresets (FWC), a novel coreset approach which generates fair synthetic representative samples along with sample-level weights to be used in downstream learning tasks. FWC aims to minimize the Wasserstein distance between the original datasets and the weighted synthetic samples while enforcing (an empirical version of) demographic parity, a prominent criterion for algorithmic fairness, via a linear constraint. We show that FWC can be thought of as a constrained version of Lloyd's algorithm for k-medians or k-means clustering. Our experiments, conducted on both synthetic and real datasets, demonstrate the scalability of our approach and highlight the competitive performance of FWC compared to existing fair clustering approaches, even when attempting to enhance the fairness of the latter through fair pre-processing techniques.

FairWASP: Fast and Optimal Fair Wasserstein Pre-processing

Recent years have seen a surge of machine learning approaches aimed at reducing disparities in model outputs across different subgroups. In many settings, training data may be used in multiple downstream applications by different users, which means it may be most effective to intervene on the training data itself. In this work, we present FairWASP, a novel pre-processing approach designed to reduce disparities in classification datasets without modifying the original data. FairWASP returns sample-level weights such that the reweighted dataset minimizes the Wasserstein distance to the original dataset while satisfying (an empirical version of) demographic parity, a popular fairness criterion. We show theoretically that integer weights are optimal, which means our method can be equivalently understood as duplicating or eliminating samples. FairWASP can therefore be used to construct datasets which can be fed into any classification method, not just methods which accept sample weights. Our work is based on reformulating the pre-processing task as a large-scale mixed-integer program (MIP), for which we propose a highly efficient algorithm based on the cutting plane method. Experiments on synthetic datasets demonstrate that our proposed optimization algorithm significantly outperforms state-of-the-art commercial solvers in solving both the MIP and its linear program relaxation. Further experiments highlight the competitive performance of FairWASP in reducing disparities while preserving accuracy in downstream classification settings.

Using Taylor-Approximated Gradients to Improve the Frank-Wolfe Method for Empirical Risk Minimization

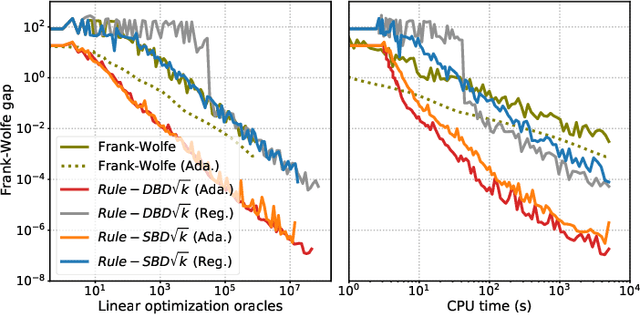
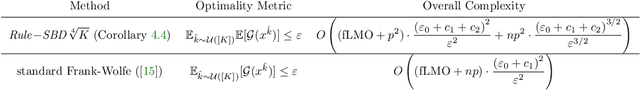
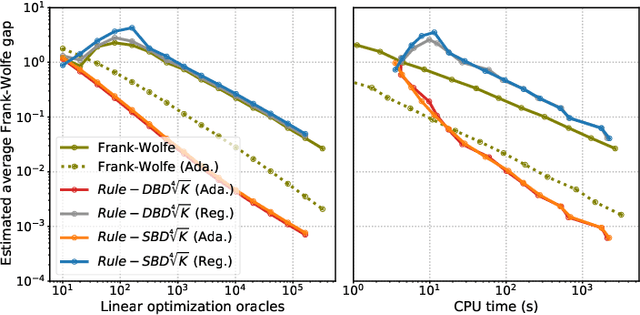
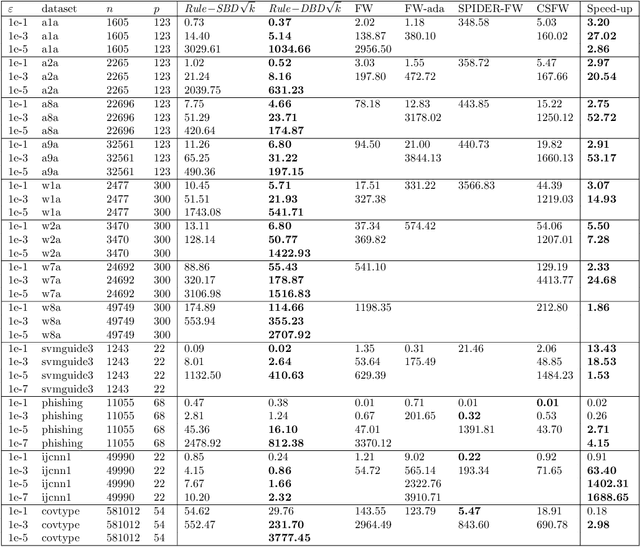
The Frank-Wolfe method has become increasingly useful in statistical and machine learning applications, due to the structure-inducing properties of the iterates, and especially in settings where linear minimization over the feasible set is more computationally efficient than projection. In the setting of Empirical Risk Minimization -- one of the fundamental optimization problems in statistical and machine learning -- the computational effectiveness of Frank-Wolfe methods typically grows linearly in the number of data observations $n$. This is in stark contrast to the case for typical stochastic projection methods. In order to reduce this dependence on $n$, we look to second-order smoothness of typical smooth loss functions (least squares loss and logistic loss, for example) and we propose amending the Frank-Wolfe method with Taylor series-approximated gradients, including variants for both deterministic and stochastic settings. Compared with current state-of-the-art methods in the regime where the optimality tolerance $\varepsilon$ is sufficiently small, our methods are able to simultaneously reduce the dependence on large $n$ while obtaining optimal convergence rates of Frank-Wolfe methods, in both the convex and non-convex settings. We also propose a novel adaptive step-size approach for which we have computational guarantees. Last of all, we present computational experiments which show that our methods exhibit very significant speed-ups over existing methods on real-world datasets for both convex and non-convex binary classification problems.

Learning from Multiple Annotator Noisy Labels via Sample-wise Label Fusion

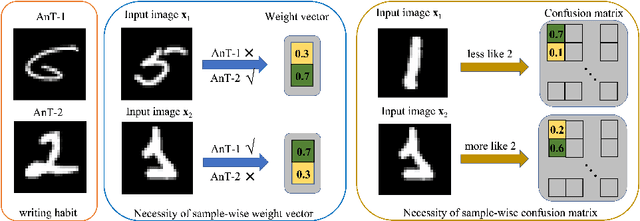
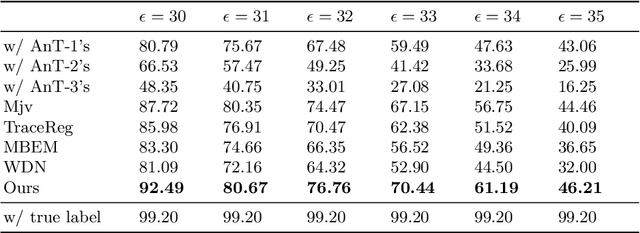
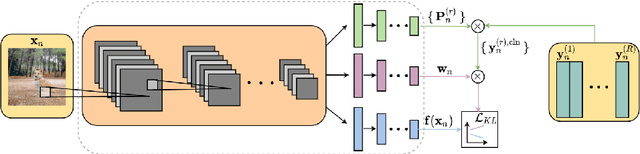
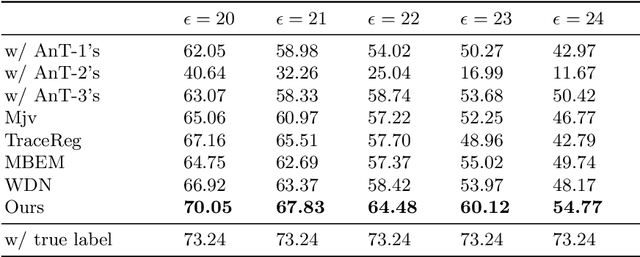
Data lies at the core of modern deep learning. The impressive performance of supervised learning is built upon a base of massive accurately labeled data. However, in some real-world applications, accurate labeling might not be viable; instead, multiple noisy labels (instead of one accurate label) are provided by several annotators for each data sample. Learning a classifier on such a noisy training dataset is a challenging task. Previous approaches usually assume that all data samples share the same set of parameters related to annotator errors, while we demonstrate that label error learning should be both annotator and data sample dependent. Motivated by this observation, we propose a novel learning algorithm. The proposed method displays superiority compared with several state-of-the-art baseline methods on MNIST, CIFAR-100, and ImageNet-100. Our code is available at: https://github.com/zhengqigao/Learning-from-Multiple-Annotator-Noisy-Labels.

Interior-point Methods Strike Back: Solving the Wasserstein Barycenter Problem

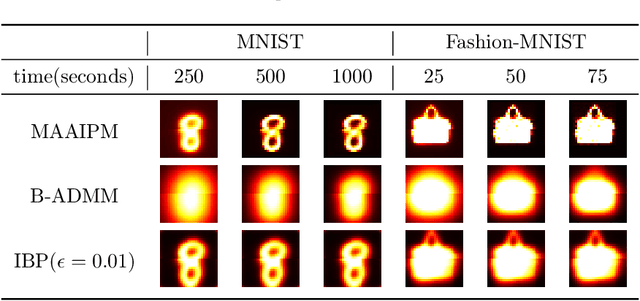
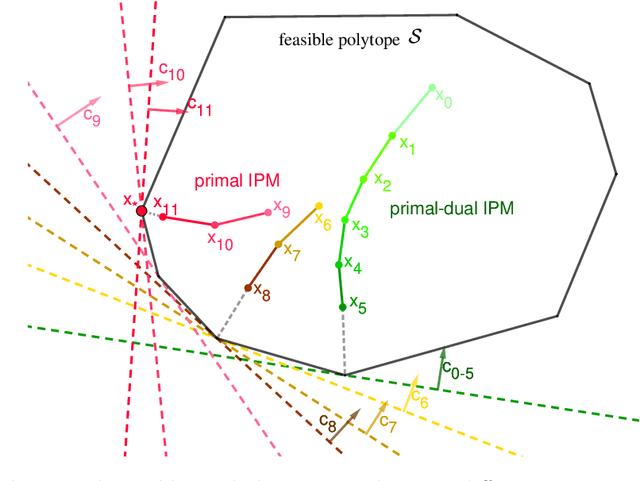
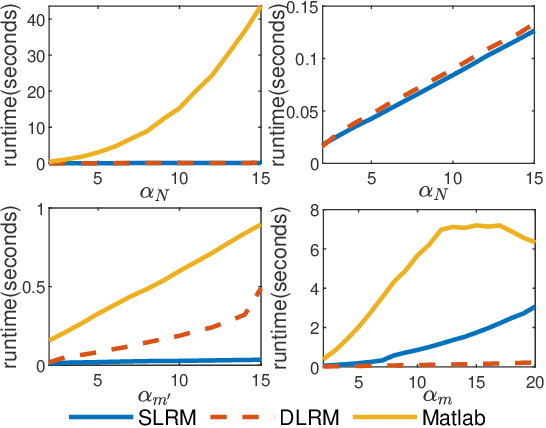
Computing the Wasserstein barycenter of a set of probability measures under the optimal transport metric can quickly become prohibitive for traditional second-order algorithms, such as interior-point methods, as the support size of the measures increases. In this paper, we overcome the difficulty by developing a new adapted interior-point method that fully exploits the problem's special matrix structure to reduce the iteration complexity and speed up the Newton procedure. Different from regularization approaches, our method achieves a well-balanced tradeoff between accuracy and speed. A numerical comparison on various distributions with existing algorithms exhibits the computational advantages of our approach. Moreover, we demonstrate the practicality of our algorithm on image benchmark problems including MNIST and Fashion-MNIST.