Using Taylor-Approximated Gradients to Improve the Frank-Wolfe Method for Empirical Risk Minimization

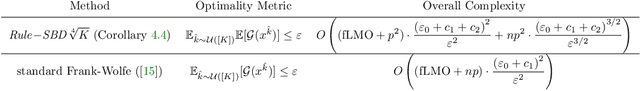
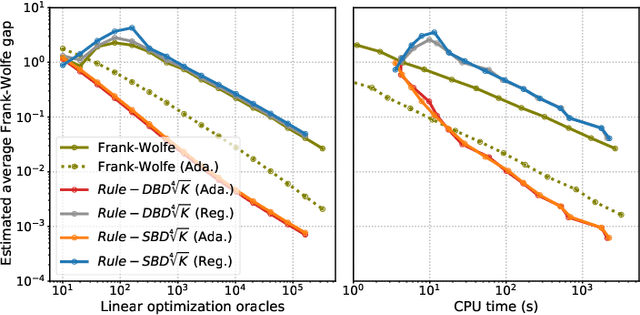
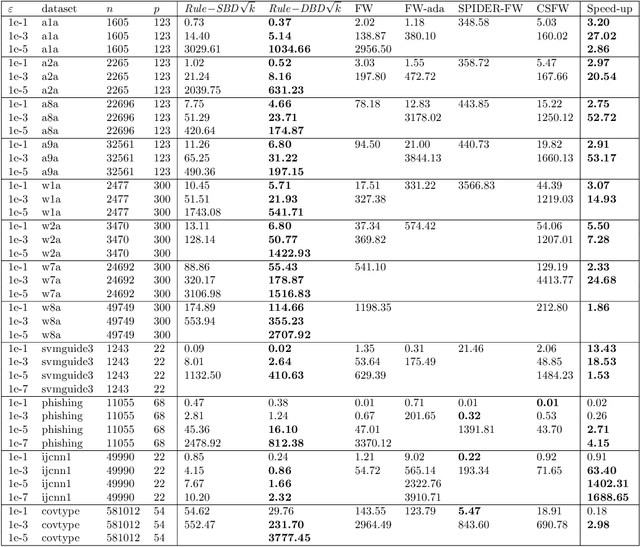
The Frank-Wolfe method has become increasingly useful in statistical and machine learning applications, due to the structure-inducing properties of the iterates, and especially in settings where linear minimization over the feasible set is more computationally efficient than projection. In the setting of Empirical Risk Minimization -- one of the fundamental optimization problems in statistical and machine learning -- the computational effectiveness of Frank-Wolfe methods typically grows linearly in the number of data observations $n$. This is in stark contrast to the case for typical stochastic projection methods. In order to reduce this dependence on $n$, we look to second-order smoothness of typical smooth loss functions (least squares loss and logistic loss, for example) and we propose amending the Frank-Wolfe method with Taylor series-approximated gradients, including variants for both deterministic and stochastic settings. Compared with current state-of-the-art methods in the regime where the optimality tolerance $\varepsilon$ is sufficiently small, our methods are able to simultaneously reduce the dependence on large $n$ while obtaining optimal convergence rates of Frank-Wolfe methods, in both the convex and non-convex settings. We also propose a novel adaptive step-size approach for which we have computational guarantees. Last of all, we present computational experiments which show that our methods exhibit very significant speed-ups over existing methods on real-world datasets for both convex and non-convex binary classification problems.

Condition Number Analysis of Logistic Regression, and its Implications for Standard First-Order Solution Methods

Logistic regression is one of the most popular methods in binary classification, wherein estimation of model parameters is carried out by solving the maximum likelihood (ML) optimization problem, and the ML estimator is defined to be the optimal solution of this problem. It is well known that the ML estimator exists when the data is non-separable, but fails to exist when the data is separable. First-order methods are the algorithms of choice for solving large-scale instances of the logistic regression problem. In this paper, we introduce a pair of condition numbers that measure the degree of non-separability or separability of a given dataset in the setting of binary classification, and we study how these condition numbers relate to and inform the properties and the convergence guarantees of first-order methods. When the training data is non-separable, we show that the degree of non-separability naturally enters the analysis and informs the properties and convergence guarantees of two standard first-order methods: steepest descent (for any given norm) and stochastic gradient descent. Expanding on the work of Bach, we also show how the degree of non-separability enters into the analysis of linear convergence of steepest descent (without needing strong convexity), as well as the adaptive convergence of stochastic gradient descent. When the training data is separable, first-order methods rather curiously have good empirical success, which is not well understood in theory. In the case of separable data, we demonstrate how the degree of separability enters into the analysis of $\ell_2$ steepest descent and stochastic gradient descent for delivering approximate-maximum-margin solutions with associated computational guarantees as well. This suggests that first-order methods can lead to statistically meaningful solutions in the separable case, even though the ML solution does not exist.

An Extended Frank-Wolfe Method with "In-Face" Directions, and its Application to Low-Rank Matrix Completion

Motivated principally by the low-rank matrix completion problem, we present an extension of the Frank-Wolfe method that is designed to induce near-optimal solutions on low-dimensional faces of the feasible region. This is accomplished by a new approach to generating ``in-face" directions at each iteration, as well as through new choice rules for selecting between in-face and ``regular" Frank-Wolfe steps. Our framework for generating in-face directions generalizes the notion of away-steps introduced by Wolfe. In particular, the in-face directions always keep the next iterate within the minimal face containing the current iterate. We present computational guarantees for the new method that trade off efficiency in computing near-optimal solutions with upper bounds on the dimension of minimal faces of iterates. We apply the new method to the matrix completion problem, where low-dimensional faces correspond to low-rank matrices. We present computational results that demonstrate the effectiveness of our methodological approach at producing nearly-optimal solutions of very low rank. On both artificial and real datasets, we demonstrate significant speed-ups in computing very low-rank nearly-optimal solutions as compared to either the Frank-Wolfe method or its traditional away-step variant.

A New Perspective on Boosting in Linear Regression via Subgradient Optimization and Relatives

In this paper we analyze boosting algorithms in linear regression from a new perspective: that of modern first-order methods in convex optimization. We show that classic boosting algorithms in linear regression, namely the incremental forward stagewise algorithm (FS$_\varepsilon$) and least squares boosting (LS-Boost($\varepsilon$)), can be viewed as subgradient descent to minimize the loss function defined as the maximum absolute correlation between the features and residuals. We also propose a modification of FS$_\varepsilon$ that yields an algorithm for the Lasso, and that may be easily extended to an algorithm that computes the Lasso path for different values of the regularization parameter. Furthermore, we show that these new algorithms for the Lasso may also be interpreted as the same master algorithm (subgradient descent), applied to a regularized version of the maximum absolute correlation loss function. We derive novel, comprehensive computational guarantees for several boosting algorithms in linear regression (including LS-Boost($\varepsilon$) and FS$_\varepsilon$) by using techniques of modern first-order methods in convex optimization. Our computational guarantees inform us about the statistical properties of boosting algorithms. In particular they provide, for the first time, a precise theoretical description of the amount of data-fidelity and regularization imparted by running a boosting algorithm with a prespecified learning rate for a fixed but arbitrary number of iterations, for any dataset.

AdaBoost and Forward Stagewise Regression are First-Order Convex Optimization Methods

Boosting methods are highly popular and effective supervised learning methods which combine weak learners into a single accurate model with good statistical performance. In this paper, we analyze two well-known boosting methods, AdaBoost and Incremental Forward Stagewise Regression (FS$_\varepsilon$), by establishing their precise connections to the Mirror Descent algorithm, which is a first-order method in convex optimization. As a consequence of these connections we obtain novel computational guarantees for these boosting methods. In particular, we characterize convergence bounds of AdaBoost, related to both the margin and log-exponential loss function, for any step-size sequence. Furthermore, this paper presents, for the first time, precise computational complexity results for FS$_\varepsilon$.