Mixup Regularization: A Probabilistic Perspective

In recent years, mixup regularization has gained popularity as an effective way to improve the generalization performance of deep learning models by training on convex combinations of training data. While many mixup variants have been explored, the proper adoption of the technique to conditional density estimation and probabilistic machine learning remains relatively unexplored. This work introduces a novel framework for mixup regularization based on probabilistic fusion that is better suited for conditional density estimation tasks. For data distributed according to a member of the exponential family, we show that likelihood functions can be analytically fused using log-linear pooling. We further propose an extension of probabilistic mixup, which allows for fusion of inputs at an arbitrary intermediate layer of the neural network. We provide a theoretical analysis comparing our approach to standard mixup variants. Empirical results on synthetic and real datasets demonstrate the benefits of our proposed framework compared to existing mixup variants.

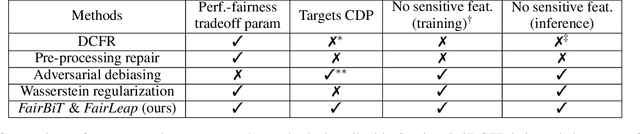
Auditing and Enforcing Conditional Fairness via Optimal Transport

Conditional demographic parity (CDP) is a measure of the demographic parity of a predictive model or decision process when conditioning on an additional feature or set of features. Many algorithmic fairness techniques exist to target demographic parity, but CDP is much harder to achieve, particularly when the conditioning variable has many levels and/or when the model outputs are continuous. The problem of auditing and enforcing CDP is understudied in the literature. In light of this, we propose novel measures of {conditional demographic disparity (CDD)} which rely on statistical distances borrowed from the optimal transport literature. We further design and evaluate regularization-based approaches based on these CDD measures. Our methods, \fairbit{} and \fairlp{}, allow us to target CDP even when the conditioning variable has many levels. When model outputs are continuous, our methods target full equality of the conditional distributions, unlike other methods that only consider first moments or related proxy quantities. We validate the efficacy of our approaches on real-world datasets.