Mixup Regularization: A Probabilistic Perspective

In recent years, mixup regularization has gained popularity as an effective way to improve the generalization performance of deep learning models by training on convex combinations of training data. While many mixup variants have been explored, the proper adoption of the technique to conditional density estimation and probabilistic machine learning remains relatively unexplored. This work introduces a novel framework for mixup regularization based on probabilistic fusion that is better suited for conditional density estimation tasks. For data distributed according to a member of the exponential family, we show that likelihood functions can be analytically fused using log-linear pooling. We further propose an extension of probabilistic mixup, which allows for fusion of inputs at an arbitrary intermediate layer of the neural network. We provide a theoretical analysis comparing our approach to standard mixup variants. Empirical results on synthetic and real datasets demonstrate the benefits of our proposed framework compared to existing mixup variants.

Distributionally and Adversarially Robust Logistic Regression via Intersecting Wasserstein Balls

Empirical risk minimization often fails to provide robustness against adversarial attacks in test data, causing poor out-of-sample performance. Adversarially robust optimization (ARO) has thus emerged as the de facto standard for obtaining models that hedge against such attacks. However, while these models are robust against adversarial attacks, they tend to suffer severely from overfitting. To address this issue for logistic regression, we study the Wasserstein distributionally robust (DR) counterpart of ARO and show that this problem admits a tractable reformulation. Furthermore, we develop a framework to reduce the conservatism of this problem by utilizing an auxiliary dataset (e.g., synthetic, external, or out-of-domain data), whenever available, with instances independently sampled from a nonidentical but related ground truth. In particular, we intersect the ambiguity set of the DR problem with another Wasserstein ambiguity set that is built using the auxiliary dataset. We analyze the properties of the underlying optimization problem, develop efficient solution algorithms, and demonstrate that the proposed method consistently outperforms benchmark approaches on real-world datasets.

Grouped sparse projection

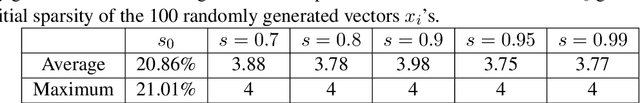
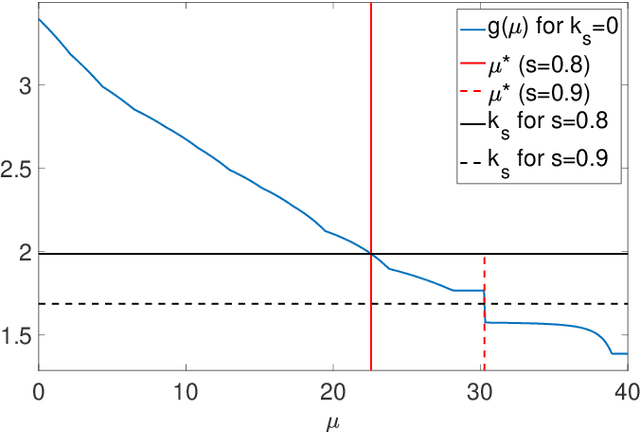
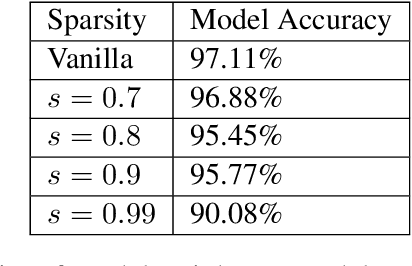
As evident from deep learning, very large models bring improvements in training dynamics and representation power. Yet, smaller models have benefits of energy efficiency and interpretability. To get the benefits from both ends of the spectrum we often encourage sparsity in the model. Unfortunately, most existing approaches do not have a controllable way to request a desired value of sparsity in an interpretable parameter. In this paper, we design a new sparse projection method for a set of vectors in order to achieve a desired average level of sparsity which is measured using the ratio of the $\ell_1$ and $\ell_2$ norms. Most existing methods project each vector individuality trying to achieve a target sparsity, hence the user has to choose a sparsity level for each vector (e.g., impose that all vectors have the same sparsity). Instead, we project all vectors together to achieve an average target sparsity, where the sparsity levels of the vectors is automatically tuned. We also propose a generalization of this projection using a new notion of weighted sparsity measured using the ratio of a weighted $\ell_1$ and the $\ell_2$ norms. These projections can be used in particular to sparsify the columns of a matrix, which we use to compute sparse nonnegative matrix factorization and to learn sparse deep networks.