Unmasking Efficiency: Learning Salient Sparse Models in Non-IID Federated Learning

In this work, we propose Salient Sparse Federated Learning (SSFL), a streamlined approach for sparse federated learning with efficient communication. SSFL identifies a sparse subnetwork prior to training, leveraging parameter saliency scores computed separately on local client data in non-IID scenarios, and then aggregated, to determine a global mask. Only the sparse model weights are communicated each round between the clients and the server. We validate SSFL's effectiveness using standard non-IID benchmarks, noting marked improvements in the sparsity--accuracy trade-offs. Finally, we deploy our method in a real-world federated learning framework and report improvement in communication time.

Learning low-dimensional dynamics from whole-brain data improves task capture

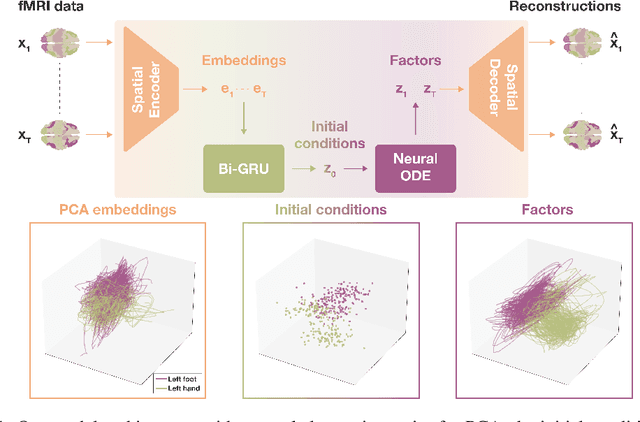
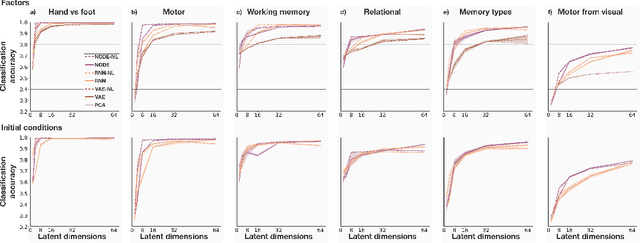
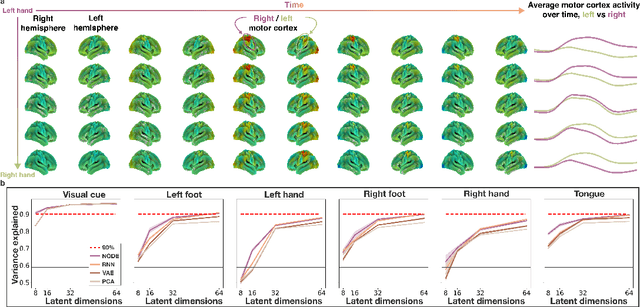
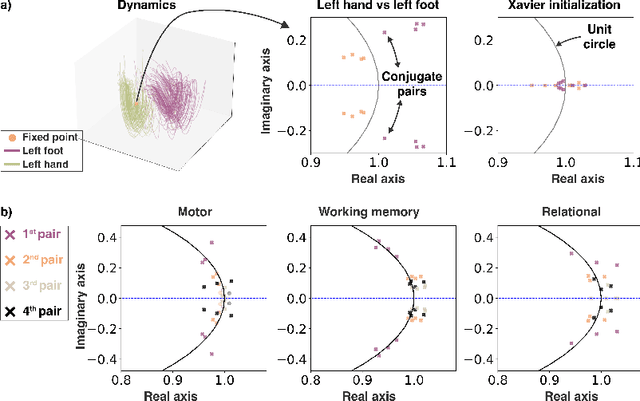
The neural dynamics underlying brain activity are critical to understanding cognitive processes and mental disorders. However, current voxel-based whole-brain dimensionality reduction techniques fall short of capturing these dynamics, producing latent timeseries that inadequately relate to behavioral tasks. To address this issue, we introduce a novel approach to learning low-dimensional approximations of neural dynamics by using a sequential variational autoencoder (SVAE) that represents the latent dynamical system via a neural ordinary differential equation (NODE). Importantly, our method finds smooth dynamics that can predict cognitive processes with accuracy higher than classical methods. Our method also shows improved spatial localization to task-relevant brain regions and identifies well-known structures such as the motor homunculus from fMRI motor task recordings. We also find that non-linear projections to the latent space enhance performance for specific tasks, offering a promising direction for future research. We evaluate our approach on various task-fMRI datasets, including motor, working memory, and relational processing tasks, and demonstrate that it outperforms widely used dimensionality reduction techniques in how well the latent timeseries relates to behavioral sub-tasks, such as left-hand or right-hand tapping. Additionally, we replace the NODE with a recurrent neural network (RNN) and compare the two approaches to understand the importance of explicitly learning a dynamical system. Lastly, we analyze the robustness of the learned dynamical systems themselves and find that their fixed points are robust across seeds, highlighting our method's potential for the analysis of cognitive processes as dynamical systems.

SalientGrads: Sparse Models for Communication Efficient and Data Aware Distributed Federated Training

Federated learning (FL) enables the training of a model leveraging decentralized data in client sites while preserving privacy by not collecting data. However, one of the significant challenges of FL is limited computation and low communication bandwidth in resource limited edge client nodes. To address this, several solutions have been proposed in recent times including transmitting sparse models and learning dynamic masks iteratively, among others. However, many of these methods rely on transmitting the model weights throughout the entire training process as they are based on ad-hoc or random pruning criteria. In this work, we propose Salient Grads, which simplifies the process of sparse training by choosing a data aware subnetwork before training, based on the model-parameter's saliency scores, which is calculated from the local client data. Moreover only highly sparse gradients are transmitted between the server and client models during the training process unlike most methods that rely on sharing the entire dense model in each round. We also demonstrate the efficacy of our method in a real world federated learning application and report improvement in wall-clock communication time.

Single-Shot Pruning for Offline Reinforcement Learning

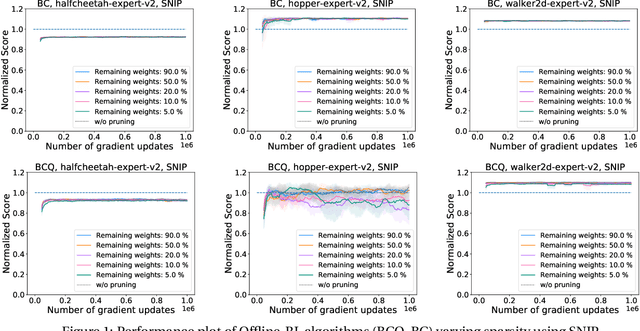
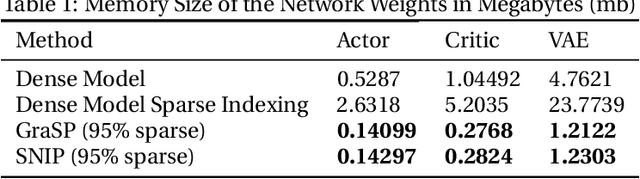
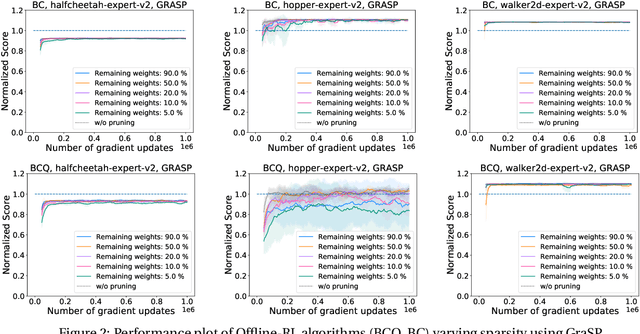
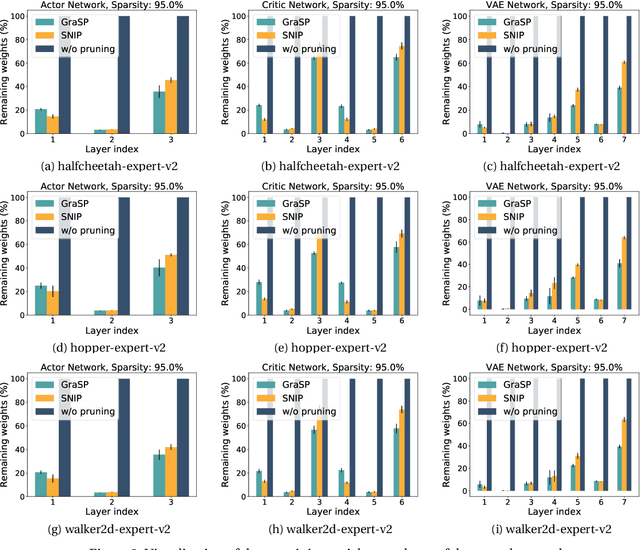
Deep Reinforcement Learning (RL) is a powerful framework for solving complex real-world problems. Large neural networks employed in the framework are traditionally associated with better generalization capabilities, but their increased size entails the drawbacks of extensive training duration, substantial hardware resources, and longer inference times. One way to tackle this problem is to prune neural networks leaving only the necessary parameters. State-of-the-art concurrent pruning techniques for imposing sparsity perform demonstrably well in applications where data distributions are fixed. However, they have not yet been substantially explored in the context of RL. We close the gap between RL and single-shot pruning techniques and present a general pruning approach to the Offline RL. We leverage a fixed dataset to prune neural networks before the start of RL training. We then run experiments varying the network sparsity level and evaluating the validity of pruning at initialization techniques in continuous control tasks. Our results show that with 95% of the network weights pruned, Offline-RL algorithms can still retain performance in the majority of our experiments. To the best of our knowledge, no prior work utilizing pruning in RL retained performance at such high levels of sparsity. Moreover, pruning at initialization techniques can be easily integrated into any existing Offline-RL algorithms without changing the learning objective.

Grouped sparse projection

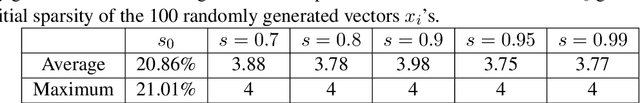
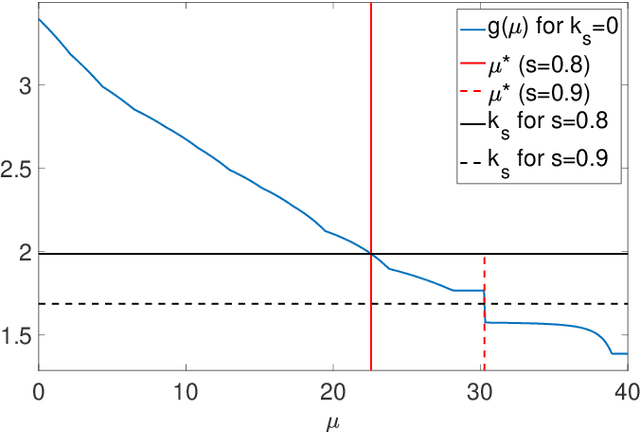
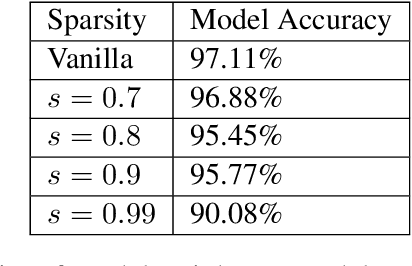
As evident from deep learning, very large models bring improvements in training dynamics and representation power. Yet, smaller models have benefits of energy efficiency and interpretability. To get the benefits from both ends of the spectrum we often encourage sparsity in the model. Unfortunately, most existing approaches do not have a controllable way to request a desired value of sparsity in an interpretable parameter. In this paper, we design a new sparse projection method for a set of vectors in order to achieve a desired average level of sparsity which is measured using the ratio of the $\ell_1$ and $\ell_2$ norms. Most existing methods project each vector individuality trying to achieve a target sparsity, hence the user has to choose a sparsity level for each vector (e.g., impose that all vectors have the same sparsity). Instead, we project all vectors together to achieve an average target sparsity, where the sparsity levels of the vectors is automatically tuned. We also propose a generalization of this projection using a new notion of weighted sparsity measured using the ratio of a weighted $\ell_1$ and the $\ell_2$ norms. These projections can be used in particular to sparsify the columns of a matrix, which we use to compute sparse nonnegative matrix factorization and to learn sparse deep networks.