Learning low-dimensional dynamics from whole-brain data improves task capture

The neural dynamics underlying brain activity are critical to understanding cognitive processes and mental disorders. However, current voxel-based whole-brain dimensionality reduction techniques fall short of capturing these dynamics, producing latent timeseries that inadequately relate to behavioral tasks. To address this issue, we introduce a novel approach to learning low-dimensional approximations of neural dynamics by using a sequential variational autoencoder (SVAE) that represents the latent dynamical system via a neural ordinary differential equation (NODE). Importantly, our method finds smooth dynamics that can predict cognitive processes with accuracy higher than classical methods. Our method also shows improved spatial localization to task-relevant brain regions and identifies well-known structures such as the motor homunculus from fMRI motor task recordings. We also find that non-linear projections to the latent space enhance performance for specific tasks, offering a promising direction for future research. We evaluate our approach on various task-fMRI datasets, including motor, working memory, and relational processing tasks, and demonstrate that it outperforms widely used dimensionality reduction techniques in how well the latent timeseries relates to behavioral sub-tasks, such as left-hand or right-hand tapping. Additionally, we replace the NODE with a recurrent neural network (RNN) and compare the two approaches to understand the importance of explicitly learning a dynamical system. Lastly, we analyze the robustness of the learned dynamical systems themselves and find that their fixed points are robust across seeds, highlighting our method's potential for the analysis of cognitive processes as dynamical systems.

CommsVAE: Learning the brain's macroscale communication dynamics using coupled sequential VAEs

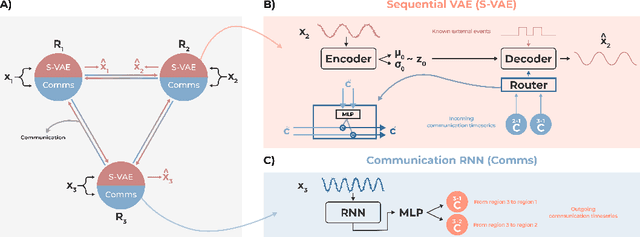
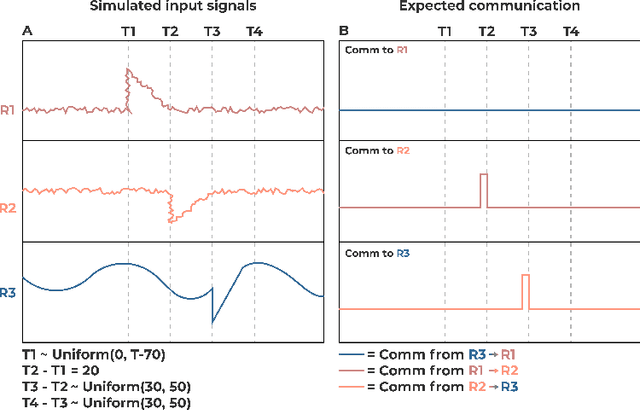
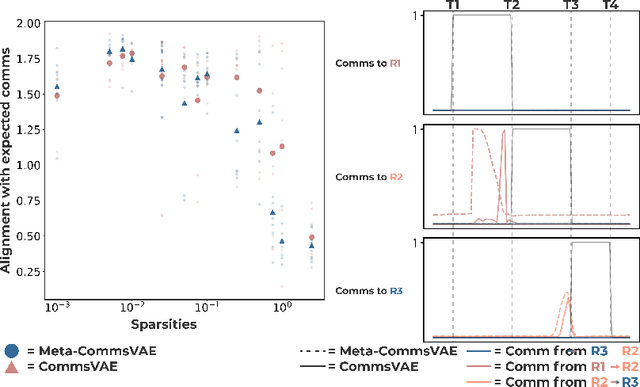
Communication within or between complex systems is commonplace in the natural sciences and fields such as graph neural networks. The brain is a perfect example of such a complex system, where communication between brain regions is constantly being orchestrated. To analyze communication, the brain is often split up into anatomical regions that each perform certain computations. These regions must interact and communicate with each other to perform tasks and support higher-level cognition. On a macroscale, these regions communicate through signal propagation along the cortex and along white matter tracts over longer distances. When and what types of signals are communicated over time is an unsolved problem and is often studied using either functional or structural data. In this paper, we propose a non-linear generative approach to communication from functional data. We address three issues with common connectivity approaches by explicitly modeling the directionality of communication, finding communication at each timestep, and encouraging sparsity. To evaluate our model, we simulate temporal data that has sparse communication between nodes embedded in it and show that our model can uncover the expected communication dynamics. Subsequently, we apply our model to temporal neural data from multiple tasks and show that our approach models communication that is more specific to each task. The specificity of our method means it can have an impact on the understanding of psychiatric disorders, which are believed to be related to highly specific communication between brain regions compared to controls. In sum, we propose a general model for dynamic communication learning on graphs, and show its applicability to a subfield of the natural sciences, with potential widespread scientific impact.

Spatio-temporally separable non-linear latent factor learning: an application to somatomotor cortex fMRI data

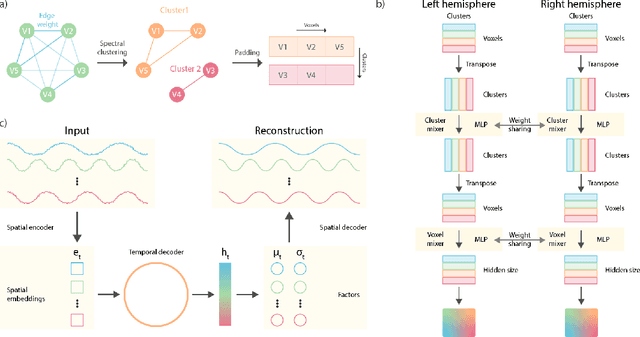
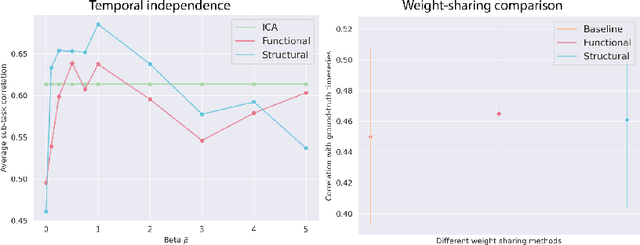
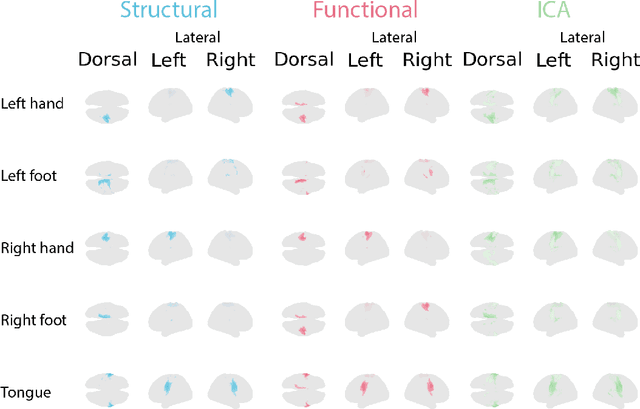
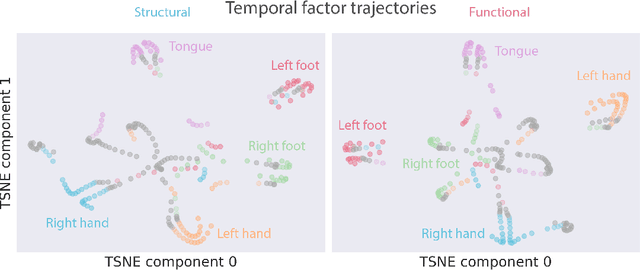
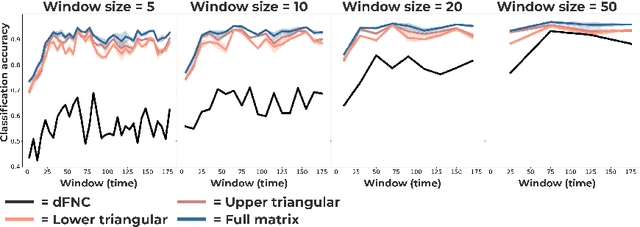
Functional magnetic resonance imaging (fMRI) data contain complex spatiotemporal dynamics, thus researchers have developed approaches that reduce the dimensionality of the signal while extracting relevant and interpretable dynamics. Models of fMRI data that can perform whole-brain discovery of dynamical latent factors are understudied. The benefits of approaches such as linear independent component analysis models have been widely appreciated, however, nonlinear extensions of these models present challenges in terms of identification. Deep learning methods provide a way forward, but new methods for efficient spatial weight-sharing are critical to deal with the high dimensionality of the data and the presence of noise. Our approach generalizes weight sharing to non-Euclidean neuroimaging data by first performing spectral clustering based on the structural and functional similarity between voxels. The spectral clusters and their assignments can then be used as patches in an adapted multi-layer perceptron (MLP)-mixer model to share parameters among input points. To encourage temporally independent latent factors, we use an additional total correlation term in the loss. Our approach is evaluated on data with multiple motor sub-tasks to assess whether the model captures disentangled latent factors that correspond to each sub-task. Then, to assess the latent factors we find further, we compare the spatial location of each latent factor to the motor homunculus. Finally, we show that our approach captures task effects better than the current gold standard of source signal separation, independent component analysis (ICA).