Interpretable Sparsification of Brain Graphs: Better Practices and Effective Designs for Graph Neural Networks

Brain graphs, which model the structural and functional relationships between brain regions, are crucial in neuroscientific and clinical applications involving graph classification. However, dense brain graphs pose computational challenges including high runtime and memory usage and limited interpretability. In this paper, we investigate effective designs in Graph Neural Networks (GNNs) to sparsify brain graphs by eliminating noisy edges. While prior works remove noisy edges based on explainability or task-irrelevant properties, their effectiveness in enhancing performance with sparsified graphs is not guaranteed. Moreover, existing approaches often overlook collective edge removal across multiple graphs. To address these issues, we introduce an iterative framework to analyze different sparsification models. Our findings are as follows: (i) methods prioritizing interpretability may not be suitable for graph sparsification as they can degrade GNNs' performance in graph classification tasks; (ii) simultaneously learning edge selection with GNN training is more beneficial than post-training; (iii) a shared edge selection across graphs outperforms separate selection for each graph; and (iv) task-relevant gradient information aids in edge selection. Based on these insights, we propose a new model, Interpretable Graph Sparsification (IGS), which enhances graph classification performance by up to 5.1% with 55.0% fewer edges. The retained edges identified by IGS provide neuroscientific interpretations and are supported by well-established literature.

Learning low-dimensional dynamics from whole-brain data improves task capture

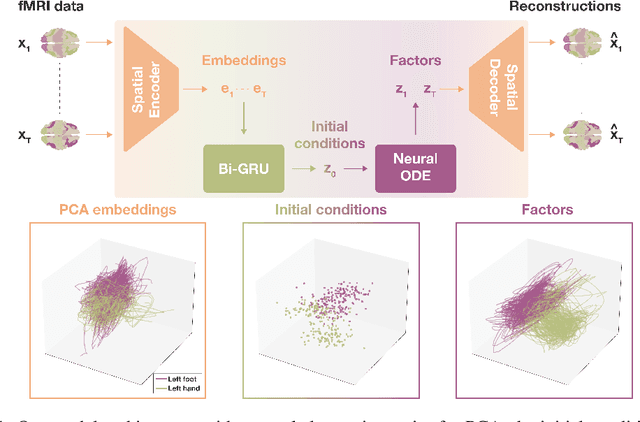
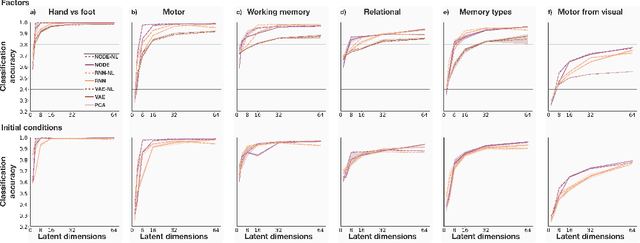
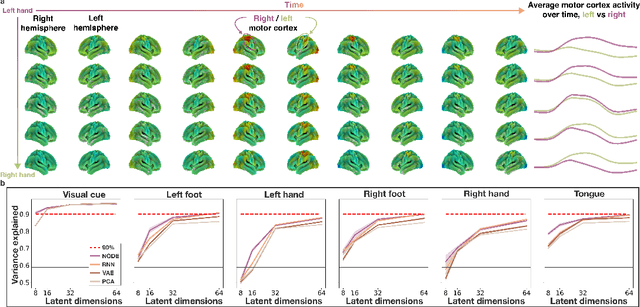
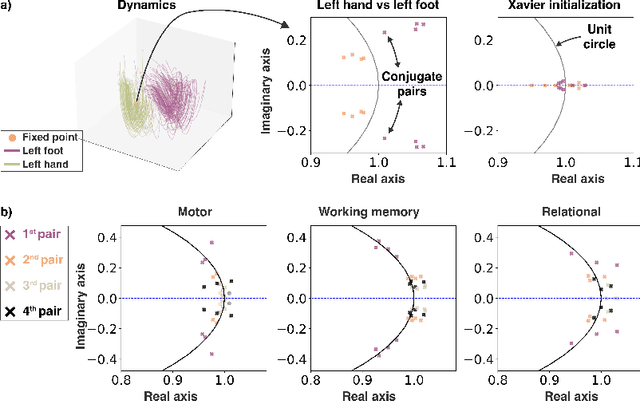
The neural dynamics underlying brain activity are critical to understanding cognitive processes and mental disorders. However, current voxel-based whole-brain dimensionality reduction techniques fall short of capturing these dynamics, producing latent timeseries that inadequately relate to behavioral tasks. To address this issue, we introduce a novel approach to learning low-dimensional approximations of neural dynamics by using a sequential variational autoencoder (SVAE) that represents the latent dynamical system via a neural ordinary differential equation (NODE). Importantly, our method finds smooth dynamics that can predict cognitive processes with accuracy higher than classical methods. Our method also shows improved spatial localization to task-relevant brain regions and identifies well-known structures such as the motor homunculus from fMRI motor task recordings. We also find that non-linear projections to the latent space enhance performance for specific tasks, offering a promising direction for future research. We evaluate our approach on various task-fMRI datasets, including motor, working memory, and relational processing tasks, and demonstrate that it outperforms widely used dimensionality reduction techniques in how well the latent timeseries relates to behavioral sub-tasks, such as left-hand or right-hand tapping. Additionally, we replace the NODE with a recurrent neural network (RNN) and compare the two approaches to understand the importance of explicitly learning a dynamical system. Lastly, we analyze the robustness of the learned dynamical systems themselves and find that their fixed points are robust across seeds, highlighting our method's potential for the analysis of cognitive processes as dynamical systems.