Distributionally and Adversarially Robust Logistic Regression via Intersecting Wasserstein Balls

Empirical risk minimization often fails to provide robustness against adversarial attacks in test data, causing poor out-of-sample performance. Adversarially robust optimization (ARO) has thus emerged as the de facto standard for obtaining models that hedge against such attacks. However, while these models are robust against adversarial attacks, they tend to suffer severely from overfitting. To address this issue for logistic regression, we study the Wasserstein distributionally robust (DR) counterpart of ARO and show that this problem admits a tractable reformulation. Furthermore, we develop a framework to reduce the conservatism of this problem by utilizing an auxiliary dataset (e.g., synthetic, external, or out-of-domain data), whenever available, with instances independently sampled from a nonidentical but related ground truth. In particular, we intersect the ambiguity set of the DR problem with another Wasserstein ambiguity set that is built using the auxiliary dataset. We analyze the properties of the underlying optimization problem, develop efficient solution algorithms, and demonstrate that the proposed method consistently outperforms benchmark approaches on real-world datasets.

Near-Optimal Fair Resource Allocation for Strategic Agents without Money: A Data-Driven Approach

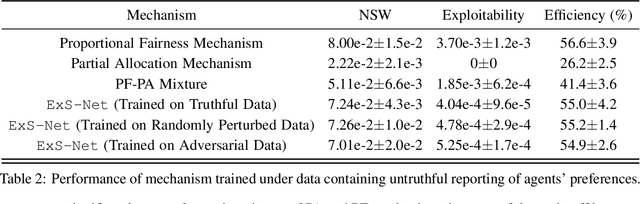
We study learning-based design of fair allocation mechanisms for divisible resources, using proportional fairness (PF) as a benchmark. The learning setting is a significant departure from the classic mechanism design literature, in that, we need to learn fair mechanisms solely from data. In particular, we consider the challenging problem of learning one-shot allocation mechanisms -- without the use of money -- that incentivize strategic agents to be truthful when reporting their valuations. It is well-known that the mechanism that directly seeks to optimize PF is not incentive compatible, meaning that the agents can potentially misreport their preferences to gain increased allocations. We introduce the notion of "exploitability" of a mechanism to measure the relative gain in utility from misreport, and make the following important contributions in the paper: (i) Using sophisticated techniques inspired by differentiable convex programming literature, we design a numerically efficient approach for computing the exploitability of the PF mechanism. This novel contribution enables us to quantify the gap that needs to be bridged to approximate PF via incentive compatible mechanisms. (ii) Next, we modify the PF mechanism to introduce a trade-off between fairness and exploitability. By properly controlling this trade-off using data, we show that our proposed mechanism, ExPF-Net, provides a strong approximation to the PF mechanism while maintaining low exploitability. This mechanism, however, comes with a high computational cost. (iii) To address the computational challenges, we propose another mechanism ExS-Net, which is end-to-end parameterized by a neural network. ExS-Net enjoys similar (slightly inferior) performance and significantly accelerated training and inference time performance. (iv) Extensive numerical simulations demonstrate the robustness and efficacy of the proposed mechanisms.

Sequential Fair Resource Allocation under a Markov Decision Process Framework

We study the sequential decision-making problem of allocating a limited resource to agents that reveal their stochastic demands on arrival over a finite horizon. Our goal is to design fair allocation algorithms that exhaust the available resource budget. This is challenging in sequential settings where information on future demands is not available at the time of decision-making. We formulate the problem as a discrete time Markov decision process (MDP). We propose a new algorithm, SAFFE, that makes fair allocations with respect to the entire demands revealed over the horizon by accounting for expected future demands at each arrival time. The algorithm introduces regularization which enables the prioritization of current revealed demands over future potential demands depending on the uncertainty in agents' future demands. Using the MDP formulation, we show that SAFFE optimizes allocations based on an upper bound on the Nash Social Welfare fairness objective, and we bound its gap to optimality with the use of concentration bounds on total future demands. Using synthetic and real data, we compare the performance of SAFFE against existing approaches and a reinforcement learning policy trained on the MDP. We show that SAFFE leads to more fair and efficient allocations and achieves close-to-optimal performance in settings with dense arrivals.