When Reasoning Hurts Legal Drafting: The Verbalization Bottleneck in Patent Claim Generation

Patent claim drafting is a challenging legal drafting task that requires technical expertise, precise linguistic control, strict adherence to formal conventions, and the preservation of complex logical relationships among claim elements. While Chain-of-Thought (CoT) prompting has been widely used to improve the reasoning capabilities of large language models (LLMs), recent evidence suggests that its benefits may be limited, or even negative, in highly structured or pattern-sensitive tasks. Therefore, this paper investigates whether CoT prompting benefits patent claim generation. We propose a task-specific CoT method for patent claim generation and evaluate its effectiveness through both automatic metrics and human expert assessment. Our results show that reasoning-enhanced prompting can improve claim quality. Moreover, we demonstrate a counter-intuitive but important empirical finding: implicit CoT, where reasoning is kept internal rather than explicitly verbalized, consistently outperforms explicit CoT. Through systematic analysis, we show that explicit CoT can introduce an unnecessary information bottleneck for claim generation. Verbalized reasoning may compromise the quality of final outputs through three specific mechanisms: abstraction of critical details, disruption of internalized generation patterns, and cascading error propagation. Our findings provide new insights into legal tasks and CoT applications.

Genie Sim 3.0 : A High-Fidelity Comprehensive Simulation Platform for Humanoid Robot

The development of robust and generalizable robot learning models is critically contingent upon the availability of large-scale, diverse training data and reliable evaluation benchmarks. Collecting data in the physical world poses prohibitive costs and scalability challenges, and prevailing simulation benchmarks frequently suffer from fragmentation, narrow scope, or insufficient fidelity to enable effective sim-to-real transfer. To address these challenges, we introduce Genie Sim 3.0, a unified simulation platform for robotic manipulation. We present Genie Sim Generator, a large language model (LLM)-powered tool that constructs high-fidelity scenes from natural language instructions. Its principal strength resides in rapid and multi-dimensional generalization, facilitating the synthesis of diverse environments to support scalable data collection and robust policy evaluation. We introduce the first benchmark that pioneers the application of LLM for automated evaluation. It leverages LLM to mass-generate evaluation scenarios and employs Vision-Language Model (VLM) to establish an automated assessment pipeline. We also release an open-source dataset comprising more than 10,000 hours of synthetic data across over 200 tasks. Through systematic experimentation, we validate the robust zero-shot sim-to-real transfer capability of our open-source dataset, demonstrating that synthetic data can server as an effective substitute for real-world data under controlled conditions for scalable policy training. For code and dataset details, please refer to: https://github.com/AgibotTech/genie_sim.

Reasoning for Hierarchical Text Classification: The Case of Patents

Hierarchical text classification (HTC) assigns documents to multiple levels of a pre-defined taxonomy. Automated patent subject classification represents one of the hardest HTC scenarios because of domain knowledge difficulty and a huge number of labels. Prior approaches only output a flat label set, which offers little insight into the reason behind predictions. Therefore, we propose Reasoning for Hierarchical Classification (RHC), a novel framework that reformulates HTC as a step-by-step reasoning task to sequentially deduce hierarchical labels. RHC trains large language models (LLMs) in two stages: a cold-start stage that aligns outputs with chain-of-thought (CoT) reasoning format and a reinforcement learning (RL) stage to enhance multi-step reasoning ability. RHC demonstrates four advantages in our experiments. (1) Effectiveness: RHC surpasses previous baselines and outperforms the supervised fine-tuning counterparts by approximately 3% in accuracy and macro F1. (2) Explainability: RHC produces natural-language justifications before prediction to facilitate human inspection. (3) Scalability: RHC scales favorably with model size with larger gains compared to standard fine-tuning. (4) Applicability: Beyond patents, we further demonstrate that RHC achieves state-of-the-art performance on other widely used HTC benchmarks, which highlights its broad applicability.

Macroscopic auxiliary asymptotic preserving neural networks for the linear radiative transfer equations

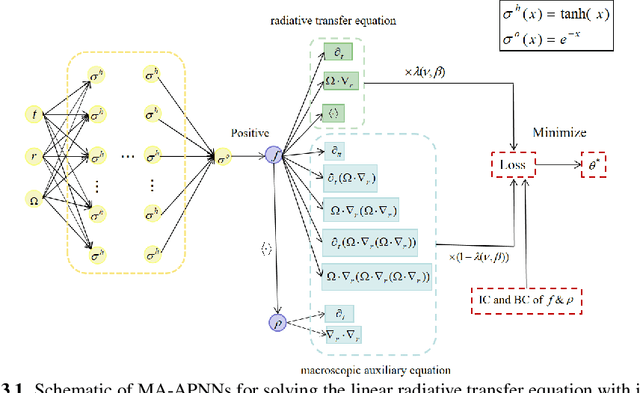
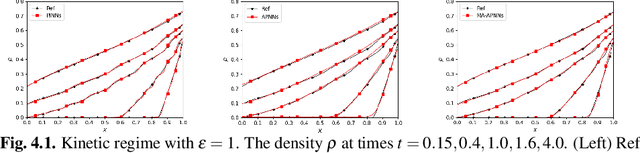
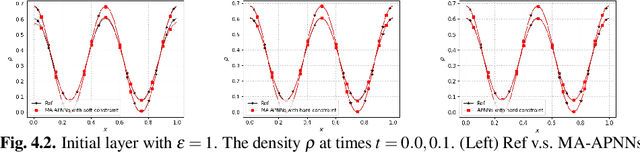
We develop a Macroscopic Auxiliary Asymptotic-Preserving Neural Network (MA-APNN) method to solve the time-dependent linear radiative transfer equations (LRTEs), which have a multi-scale nature and high dimensionality. To achieve this, we utilize the Physics-Informed Neural Networks (PINNs) framework and design a new adaptive exponentially weighted Asymptotic-Preserving (AP) loss function, which incorporates the macroscopic auxiliary equation that is derived from the original transfer equation directly and explicitly contains the information of the diffusion limit equation. Thus, as the scale parameter tends to zero, the loss function gradually transitions from the transport state to the diffusion limit state. In addition, the initial data, boundary conditions, and conservation laws serve as the regularization terms for the loss. We present several numerical examples to demonstrate the effectiveness of MA-APNNs.

A model-data asymptotic-preserving neural network method based on micro-macro decomposition for gray radiative transfer equations

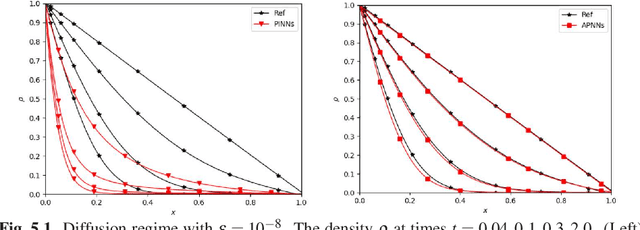
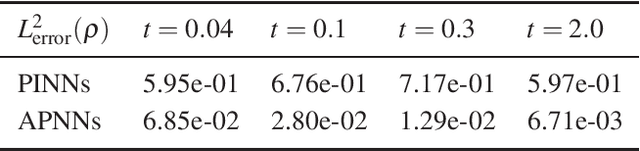
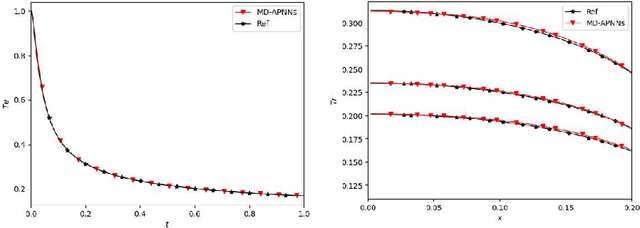
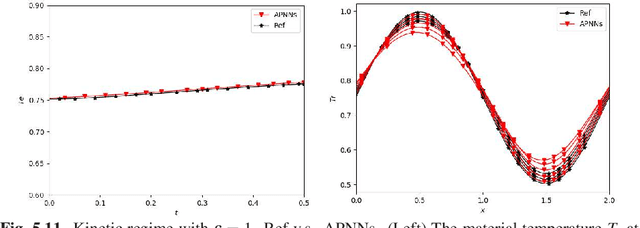
We propose a model-data asymptotic-preserving neural network(MD-APNN) method to solve the nonlinear gray radiative transfer equations(GRTEs). The system is challenging to be simulated with both the traditional numerical schemes and the vanilla physics-informed neural networks(PINNs) due to the multiscale characteristics. Under the framework of PINNs, we employ a micro-macro decomposition technique to construct a new asymptotic-preserving(AP) loss function, which includes the residual of the governing equations in the micro-macro coupled form, the initial and boundary conditions with additional diffusion limit information, the conservation laws, and a few labeled data. A convergence analysis is performed for the proposed method, and a number of numerical examples are presented to illustrate the efficiency of MD-APNNs, and particularly, the importance of the AP property in the neural networks for the diffusion dominating problems. The numerical results indicate that MD-APNNs lead to a better performance than APNNs or pure data-driven networks in the simulation of the nonlinear non-stationary GRTEs.