A model-data asymptotic-preserving neural network method based on micro-macro decomposition for gray radiative transfer equations
Paper and Code
Dec 11, 2022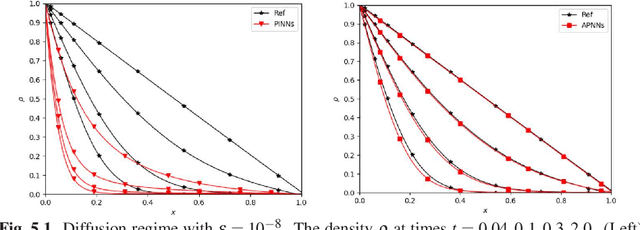
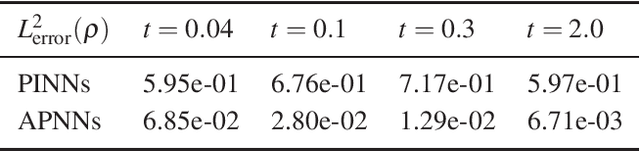
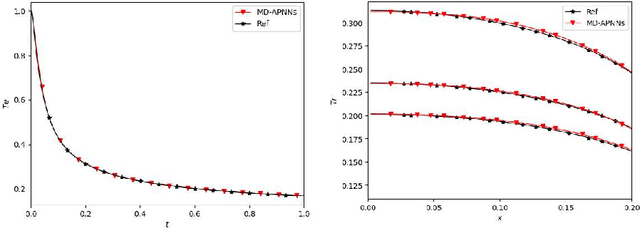
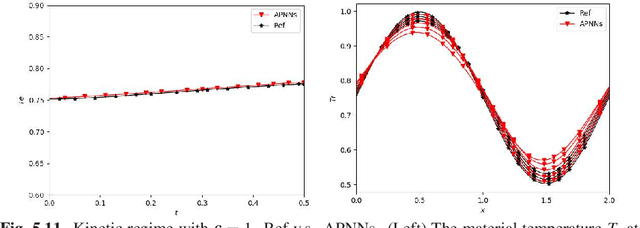
We propose a model-data asymptotic-preserving neural network(MD-APNN) method to solve the nonlinear gray radiative transfer equations(GRTEs). The system is challenging to be simulated with both the traditional numerical schemes and the vanilla physics-informed neural networks(PINNs) due to the multiscale characteristics. Under the framework of PINNs, we employ a micro-macro decomposition technique to construct a new asymptotic-preserving(AP) loss function, which includes the residual of the governing equations in the micro-macro coupled form, the initial and boundary conditions with additional diffusion limit information, the conservation laws, and a few labeled data. A convergence analysis is performed for the proposed method, and a number of numerical examples are presented to illustrate the efficiency of MD-APNNs, and particularly, the importance of the AP property in the neural networks for the diffusion dominating problems. The numerical results indicate that MD-APNNs lead to a better performance than APNNs or pure data-driven networks in the simulation of the nonlinear non-stationary GRTEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge