Conjugate-Gradient-like Based Adaptive Moment Estimation Optimization Algorithm for Deep Learning

Training deep neural networks is a challenging task. In order to speed up training and enhance the performance of deep neural networks, we rectify the vanilla conjugate gradient as conjugate-gradient-like and incorporate it into the generic Adam, and thus propose a new optimization algorithm named CG-like-Adam for deep learning. Specifically, both the first-order and the second-order moment estimation of generic Adam are replaced by the conjugate-gradient-like. Convergence analysis handles the cases where the exponential moving average coefficient of the first-order moment estimation is constant and the first-order moment estimation is unbiased. Numerical experiments show the superiority of the proposed algorithm based on the CIFAR10/100 dataset.

Macroscopic auxiliary asymptotic preserving neural networks for the linear radiative transfer equations

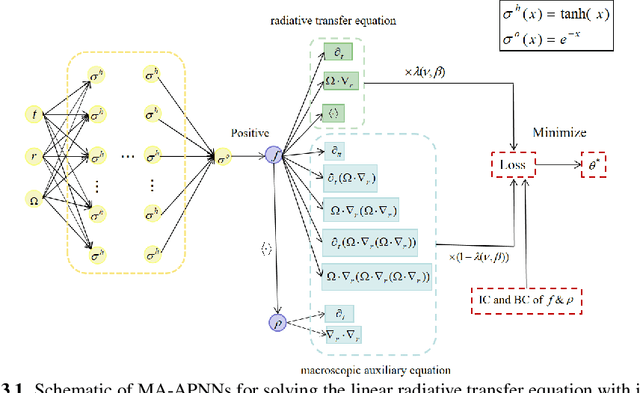
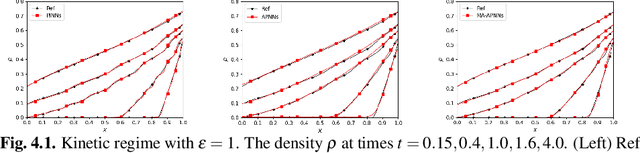
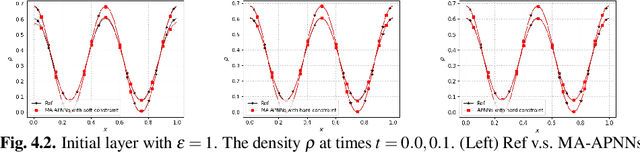
We develop a Macroscopic Auxiliary Asymptotic-Preserving Neural Network (MA-APNN) method to solve the time-dependent linear radiative transfer equations (LRTEs), which have a multi-scale nature and high dimensionality. To achieve this, we utilize the Physics-Informed Neural Networks (PINNs) framework and design a new adaptive exponentially weighted Asymptotic-Preserving (AP) loss function, which incorporates the macroscopic auxiliary equation that is derived from the original transfer equation directly and explicitly contains the information of the diffusion limit equation. Thus, as the scale parameter tends to zero, the loss function gradually transitions from the transport state to the diffusion limit state. In addition, the initial data, boundary conditions, and conservation laws serve as the regularization terms for the loss. We present several numerical examples to demonstrate the effectiveness of MA-APNNs.

Learning More Discriminative Local Descriptors for Few-shot Learning

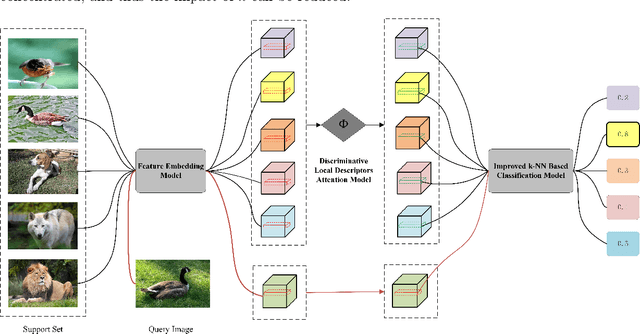
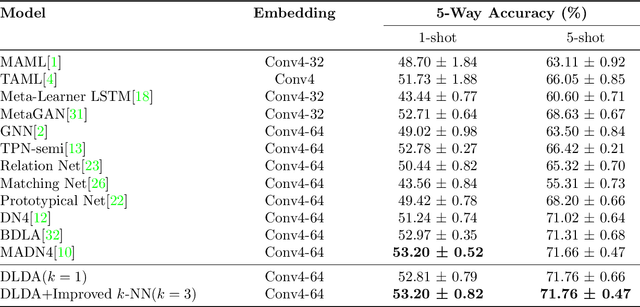
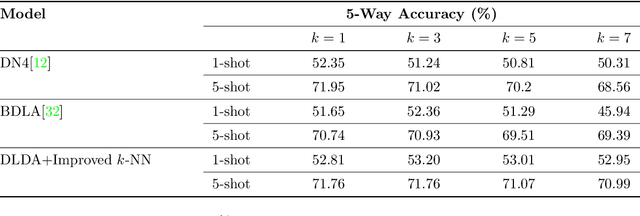
Few-shot learning for image classification comes up as a hot topic in computer vision, which aims at fast learning from a limited number of labeled images and generalize over the new tasks. In this paper, motivated by the idea of Fisher Score, we propose a Discriminative Local Descriptors Attention (DLDA) model that adaptively selects the representative local descriptors and does not introduce any additional parameters, while most of the existing local descriptors based methods utilize the neural networks that inevitably involve the tedious parameter tuning. Moreover, we modify the traditional $k$-NN classification model by adjusting the weights of the $k$ nearest neighbors according to their distances from the query point. Experiments on four benchmark datasets show that our method not only achieves higher accuracy compared with the state-of-art approaches for few-shot learning, but also possesses lower sensitivity to the choices of $k$.

A model-data asymptotic-preserving neural network method based on micro-macro decomposition for gray radiative transfer equations

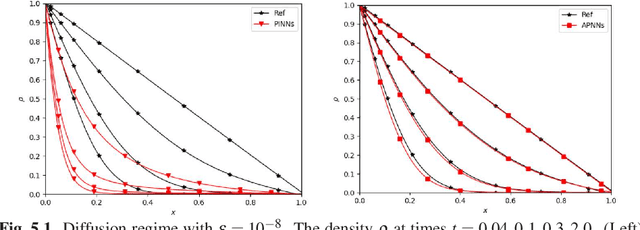
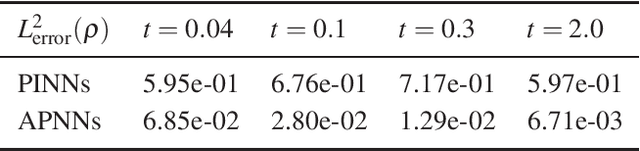
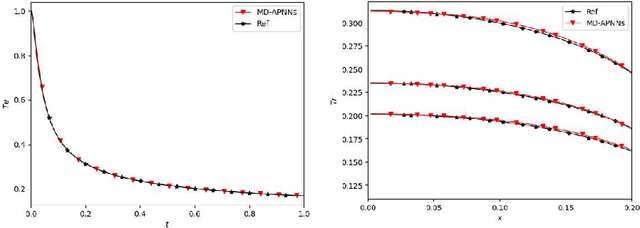
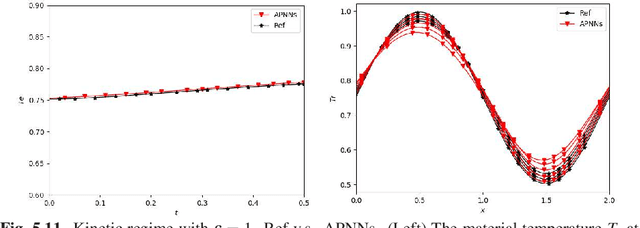
We propose a model-data asymptotic-preserving neural network(MD-APNN) method to solve the nonlinear gray radiative transfer equations(GRTEs). The system is challenging to be simulated with both the traditional numerical schemes and the vanilla physics-informed neural networks(PINNs) due to the multiscale characteristics. Under the framework of PINNs, we employ a micro-macro decomposition technique to construct a new asymptotic-preserving(AP) loss function, which includes the residual of the governing equations in the micro-macro coupled form, the initial and boundary conditions with additional diffusion limit information, the conservation laws, and a few labeled data. A convergence analysis is performed for the proposed method, and a number of numerical examples are presented to illustrate the efficiency of MD-APNNs, and particularly, the importance of the AP property in the neural networks for the diffusion dominating problems. The numerical results indicate that MD-APNNs lead to a better performance than APNNs or pure data-driven networks in the simulation of the nonlinear non-stationary GRTEs.

Big-Data Clustering: K-Means or K-Indicators?

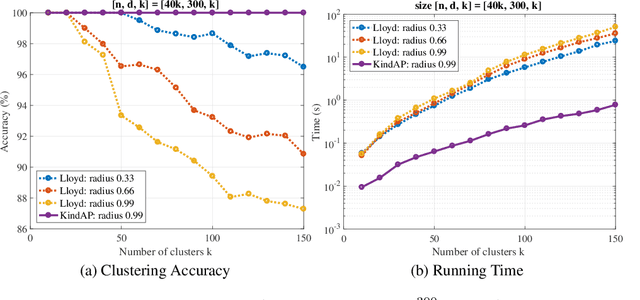
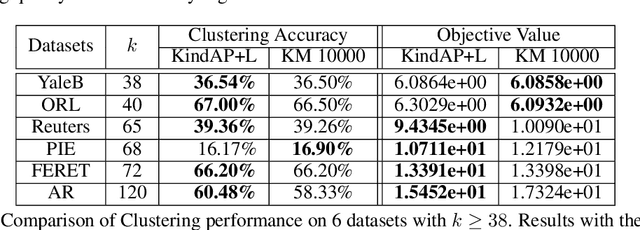
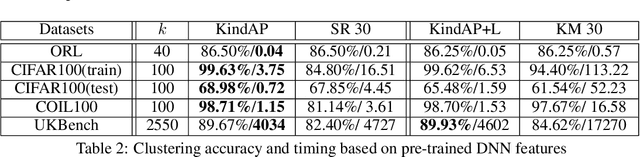
The K-means algorithm is arguably the most popular data clustering method, commonly applied to processed datasets in some "feature spaces", as is in spectral clustering. Highly sensitive to initializations, however, K-means encounters a scalability bottleneck with respect to the number of clusters K as this number grows in big data applications. In this work, we promote a closely related model called K-indicators model and construct an efficient, semi-convex-relaxation algorithm that requires no randomized initializations. We present extensive empirical results to show advantages of the new algorithm when K is large. In particular, using the new algorithm to start the K-means algorithm, without any replication, can significantly outperform the standard K-means with a large number of currently state-of-the-art random replications.