Early Risk Assessment Model for ICA Timing Strategy in Unstable Angina Patients Using Multi-Modal Machine Learning

Background: Invasive coronary arteriography (ICA) is recognized as the gold standard for diagnosing cardiovascular diseases, including unstable angina (UA). The challenge lies in determining the optimal timing for ICA in UA patients, balancing the need for revascularization in high-risk patients against the potential complications in low-risk ones. Unlike myocardial infarction, UA does not have specific indicators like ST-segment deviation or cardiac enzymes, making risk assessment complex. Objectives: Our study aims to enhance the early risk assessment for UA patients by utilizing machine learning algorithms. These algorithms can potentially identify patients who would benefit most from ICA by analyzing less specific yet related indicators that are challenging for human physicians to interpret. Methods: We collected data from 640 UA patients at Shanghai General Hospital, including medical history and electrocardiograms (ECG). Machine learning algorithms were trained using multi-modal demographic characteristics including clinical risk factors, symptoms, biomarker levels, and ECG features extracted by pre-trained neural networks. The goal was to stratify patients based on their revascularization risk. Additionally, we translated our models into applicable and explainable look-up tables through discretization for practical clinical use. Results: The study achieved an Area Under the Curve (AUC) of $0.719 \pm 0.065$ in risk stratification, significantly surpassing the widely adopted GRACE score's AUC of $0.579 \pm 0.044$. Conclusions: The results suggest that machine learning can provide superior risk stratification for UA patients. This improved stratification could help in balancing the risks, costs, and complications associated with ICA, indicating a potential shift in clinical assessment practices for unstable angina.

Characteristic Guidance: Non-linear Correction for Diffusion Model at Large Guidance Scale

Popular guidance for denoising diffusion probabilistic model (DDPM) linearly combines distinct conditional models together to provide enhanced control over samples. However, this approach overlooks nonlinear effects that become significant when guidance scale is large. To address this issue, we propose characteristic guidance, a sampling method that provides first-principle non-linear correction for classifier-free guided DDPMs. Such correction forces the guided DDPMs to respect the Fokker-Planck equation of their underlying diffusion process, in a way that is training-free, derivative-free, and compatible with existing sampling methods. Experiments show that characteristic guidance enhances control and reduces color and exposure issues in image generation, proving effective in diverse applications ranging from latent space sampling to solving physics problems like magnet phase transitions.

Stabilizing the Maximal Entropy Moment Method for Rarefied Gas Dynamics at Single-Precision

Developing extended hydrodynamics equations valid for both dense and rarefied gases remains a great challenge. A systematical solution for this challenge is the moment method describing both dense and rarefied gas behaviors with moments of gas molecule velocity distributions. Among moment methods, the maximal entropy moment method (MEM) stands out for its well-posedness and stability, which utilizes velocity distributions with maximized entropy. However, finding such distributions requires solving an ill-conditioned and computation-demanding optimization problem. This problem causes numerical overflow and breakdown when the numerical precision is insufficient, especially for flows like high-speed shock waves. It also prevents modern GPUs from accelerating optimization with their enormous single floating-point precision computation power. This paper aims to stabilize MEM, making it practical for simulating very strong normal shock waves on modern GPUs at single precision. We propose the gauge transformations for MEM, making the optimization less ill-conditioned. We also tackle numerical overflow and breakdown by adopting the canonical form of distribution and Newton's modified optimization method. With these techniques, we achieved a single-precision GPU simulation of a Mach 10 shock wave with 35 moments MEM, surpassing the previous double-precision results of Mach 4. Moreover, we argued that over-refined spatial mesh degrades both the accuracy and stability of MEM. Overall, this paper makes the maximal entropy moment method practical for simulating very strong normal shock waves on modern GPUs at single-precision, with significant stability improvement compared to previous methods.

Data Driven Macroscopic Modeling across Knudsen Numbers for Rarefied Gas Dynamics and Application to Rayleigh Scattering

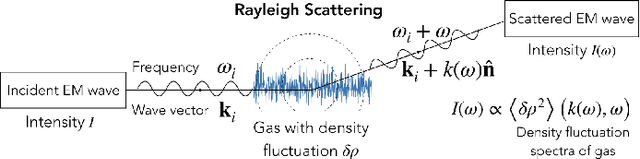
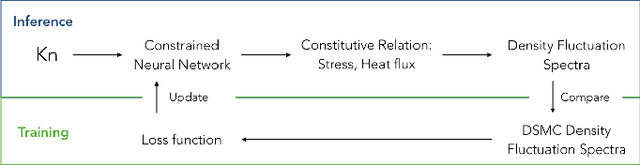
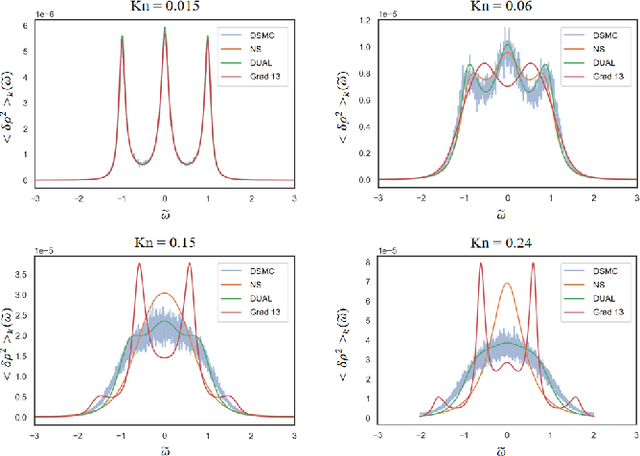
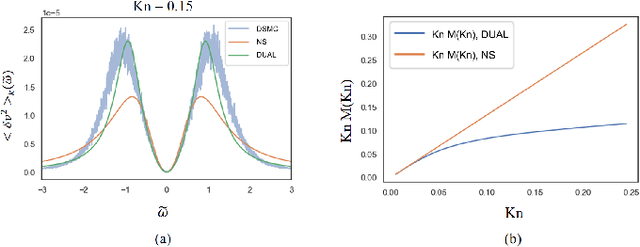
Macroscopic modeling of the gas dynamics across Knudsen numbers from dense gas region to rarefied gas region remains a great challenge. The reason is macroscopic models lack accurate constitutive relations valid across different Knudsen numbers. To address this problem, we proposed a Data-driven, KnUdsen number Adaptive Linear constitutive relation model named DUAL. The DUAL model is accurate across a range of Knudsen numbers, from dense to rarefied, through learning to adapt Knudsen number change from observed data. It is consistent with the Navier-Stokes equation under the hydrodynamic limit, by utilizing a constrained neural network. In addition, it naturally satisfies the second law of thermodynamics and is robust to noisy data. We test the DUAL model on the calculation of Rayleigh scattering spectra. The DUAL model gives accurate spectra for various Knudsen numbers and is superior to traditional perturbation and moment expansion methods.