PiRD: Physics-informed Residual Diffusion for Flow Field Reconstruction

The use of machine learning in fluid dynamics is becoming more common to expedite the computation when solving forward and inverse problems of partial differential equations. Yet, a notable challenge with existing convolutional neural network (CNN)-based methods for data fidelity enhancement is their reliance on specific low-fidelity data patterns and distributions during the training phase. In addition, the CNN-based method essentially treats the flow reconstruction task as a computer vision task that prioritizes the element-wise precision which lacks a physical and mathematical explanation. This dependence can dramatically affect the models' effectiveness in real-world scenarios, especially when the low-fidelity input deviates from the training data or contains noise not accounted for during training. The introduction of diffusion models in this context shows promise for improving performance and generalizability. Unlike direct mapping from a specific low-fidelity to a high-fidelity distribution, diffusion models learn to transition from any low-fidelity distribution towards a high-fidelity one. Our proposed model - Physics-informed Residual Diffusion, demonstrates the capability to elevate the quality of data from both standard low-fidelity inputs, to low-fidelity inputs with injected Gaussian noise, and randomly collected samples. By integrating physics-based insights into the objective function, it further refines the accuracy and the fidelity of the inferred high-quality data. Experimental results have shown that our approach can effectively reconstruct high-quality outcomes for two-dimensional turbulent flows from a range of low-fidelity input conditions without requiring retraining.

Accelerated Distributed Aggregative Optimization

In this paper, we investigate a distributed aggregative optimization problem in a network, where each agent has its own local cost function which depends not only on the local state variable but also on an aggregated function of state variables from all agents. To accelerate the optimization process, we combine heavy ball and Nesterov's accelerated methods with distributed aggregative gradient tracking, and propose two novel algorithms named DAGT-HB and DAGT-NES for solving the distributed aggregative optimization problem. We analyse that the DAGT-HB and DAGT-NES algorithms can converge to an optimal solution at a global $\mathbf{R}-$linear convergence rate when the objective function is smooth and strongly convex, and when the parameters (e.g., step size and momentum coefficients) are selected within certain ranges. A numerical experiment on the optimal placement problem is given to verify the effectiveness and superiority of our proposed algorithms.

The Novel Adaptive Fractional Order Gradient Decent Algorithms Design via Robust Control

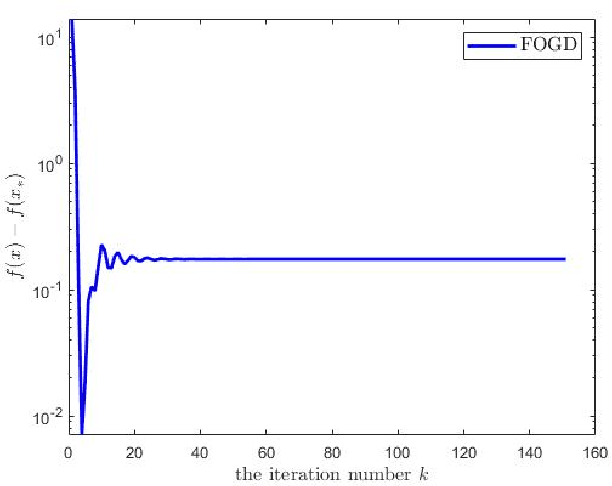
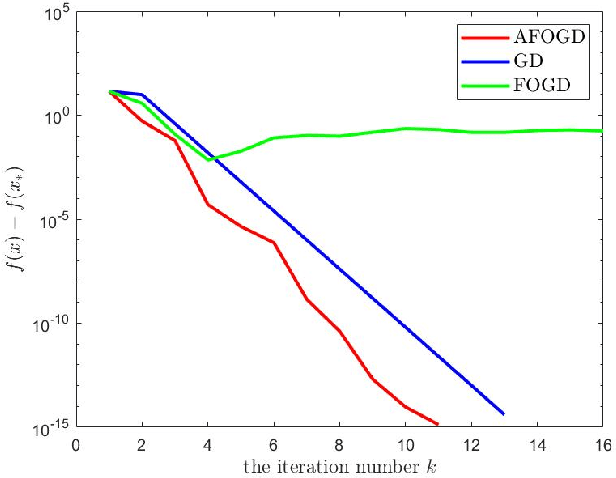
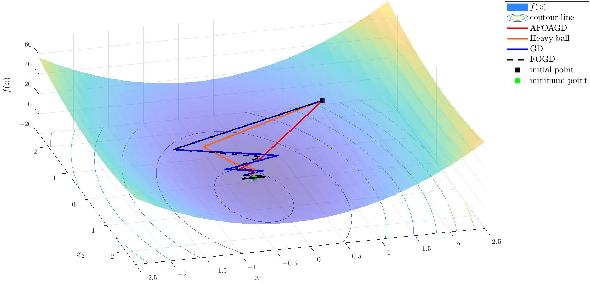
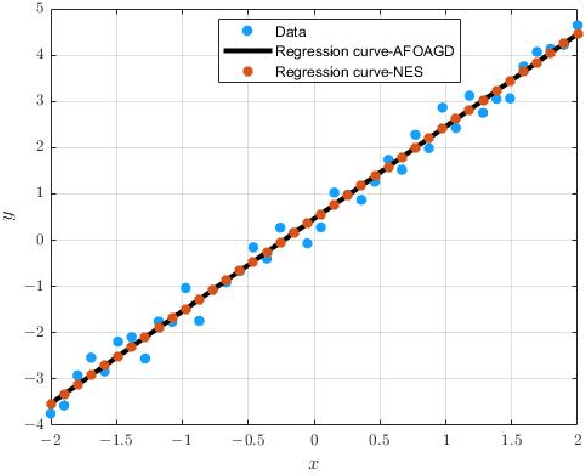
The vanilla fractional order gradient descent may oscillatively converge to a region around the global minimum instead of converging to the exact minimum point, or even diverge, in the case where the objective function is strongly convex. To address this problem, a novel adaptive fractional order gradient descent (AFOGD) method and a novel adaptive fractional order accelerated gradient descent (AFOAGD) method are proposed in this paper. Inspired by the quadratic constraints and Lyapunov stability analysis from robust control theory, we establish a linear matrix inequality to analyse the convergence of our proposed algorithms. We prove that the proposed algorithms can achieve R-linear convergence when the objective function is $\textbf{L-}$smooth and $\textbf{m-}$strongly-convex. Several numerical simulations are demonstrated to verify the effectiveness and superiority of our proposed algorithms.

GotFlow3D: Recurrent Graph Optimal Transport for Learning 3D Flow Motion in Particle Tracking

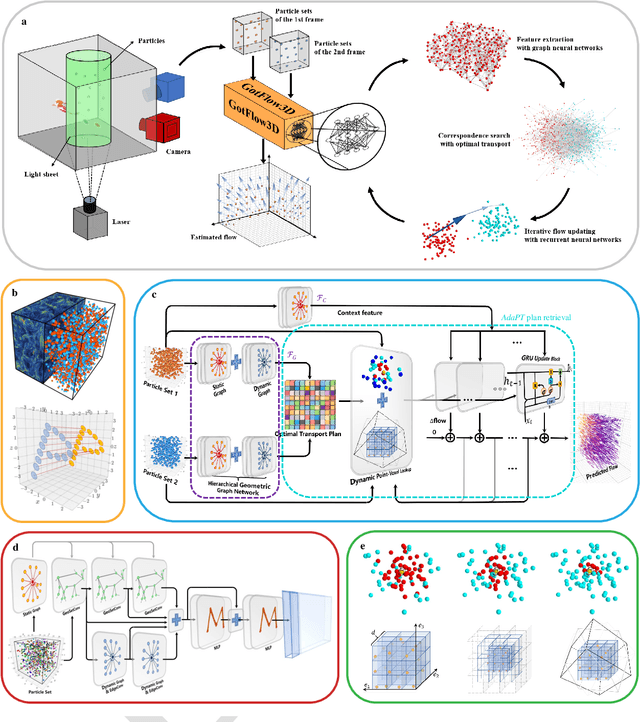
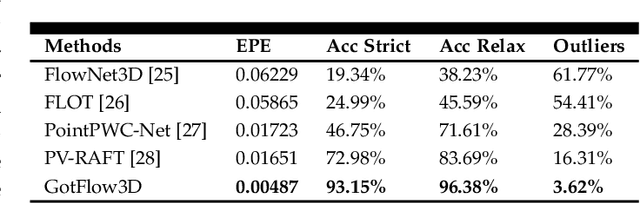
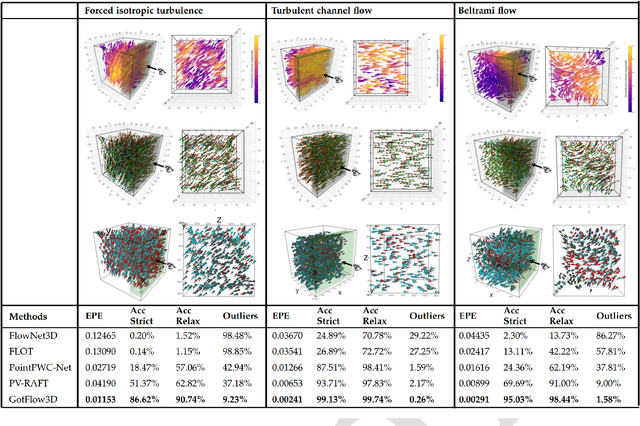
Flow visualization technologies such as particle tracking velocimetry (PTV) are broadly used in understanding the all-pervasiveness three-dimensional (3D) turbulent flow from nature and industrial processes. Despite the advances in 3D acquisition techniques, the developed motion estimation algorithms in particle tracking remain great challenges of large particle displacements, dense particle distributions and high computational cost. By introducing a novel deep neural network based on recurrent Graph Optimal Transport, called GotFlow3D, we present an end-to-end solution to learn the 3D fluid flow motion from double-frame particle sets. The proposed network constructs two graphs in the geometric and feature space and further enriches the original particle representations with the fused intrinsic and extrinsic features learnt from a graph neural network. The extracted deep features are subsequently utilized to make optimal transport plans indicating the correspondences of particle pairs, which are then iteratively and adaptively retrieved to guide the recurrent flow learning. Experimental evaluations, including assessments on numerical experiments and validations on real-world experiments, demonstrate that the proposed GotFlow3D achieves state-of-the-art performance against both recently-developed scene flow learners and particle tracking algorithms, with impressive accuracy, robustness and generalization ability, which can provide deeper insight into the complex dynamics of broad physical and biological systems.

AOSLO-net: A deep learning-based method for automatic segmentation of retinal microaneurysms from adaptive optics scanning laser ophthalmoscope images

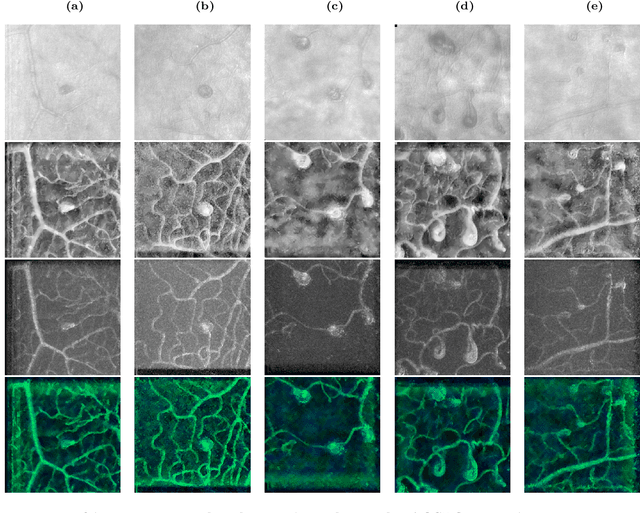
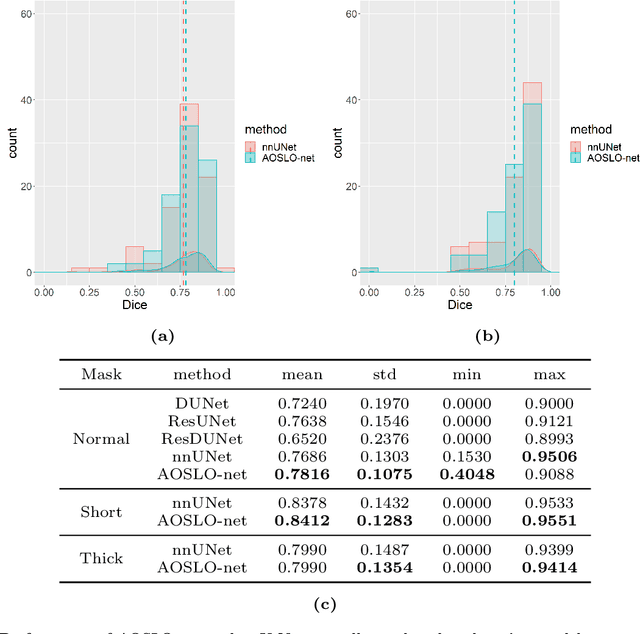
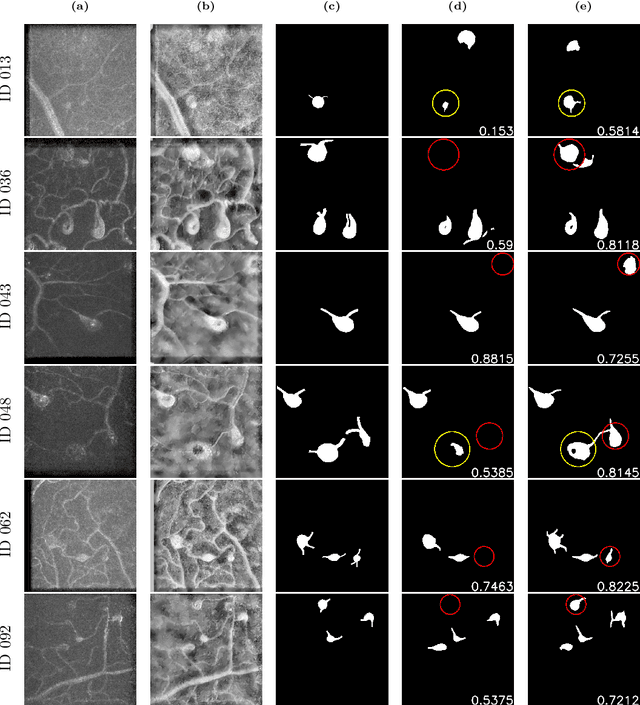
Microaneurysms (MAs) are one of the earliest signs of diabetic retinopathy (DR), a frequent complication of diabetes that can lead to visual impairment and blindness. Adaptive optics scanning laser ophthalmoscopy (AOSLO) provides real-time retinal images with resolution down to 2 $\mu m$ and thus allows detection of the morphologies of individual MAs, a potential marker that might dictate MA pathology and affect the progression of DR. In contrast to the numerous automatic models developed for assessing the number of MAs on fundus photographs, currently there is no high throughput image protocol available for automatic analysis of AOSLO photographs. To address this urgency, we introduce AOSLO-net, a deep neural network framework with customized training policies to automatically segment MAs from AOSLO images. We evaluate the performance of AOSLO-net using 87 DR AOSLO images and our results demonstrate that the proposed model outperforms the state-of-the-art segmentation model both in accuracy and cost and enables correct MA morphological classification.

Physics-informed neural networks (PINNs) for fluid mechanics: A review

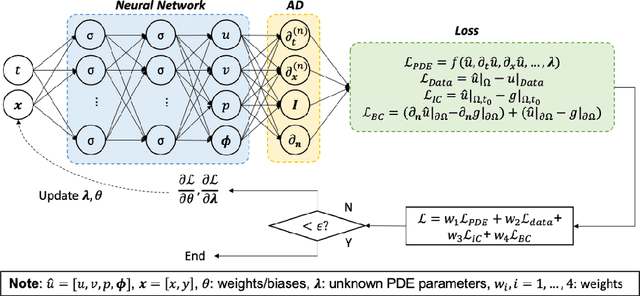
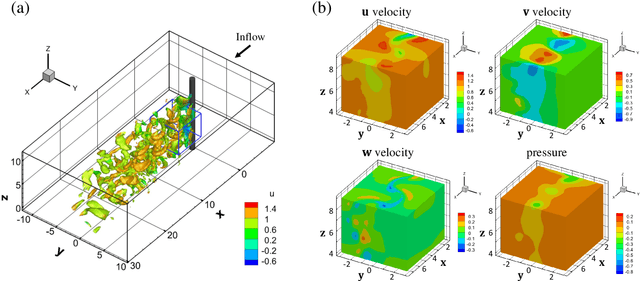
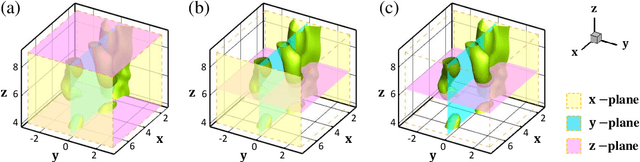
Despite the significant progress over the last 50 years in simulating flow problems using numerical discretization of the Navier-Stokes equations (NSE), we still cannot incorporate seamlessly noisy data into existing algorithms, mesh-generation is complex, and we cannot tackle high-dimensional problems governed by parametrized NSE. Moreover, solving inverse flow problems is often prohibitively expensive and requires complex and expensive formulations and new computer codes. Here, we review flow physics-informed learning, integrating seamlessly data and mathematical models, and implementing them using physics-informed neural networks (PINNs). We demonstrate the effectiveness of PINNs for inverse problems related to three-dimensional wake flows, supersonic flows, and biomedical flows.