The Novel Adaptive Fractional Order Gradient Decent Algorithms Design via Robust Control
Paper and Code
Mar 08, 2023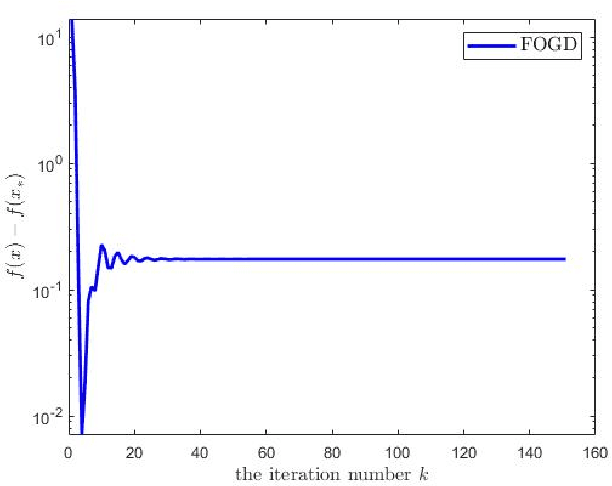
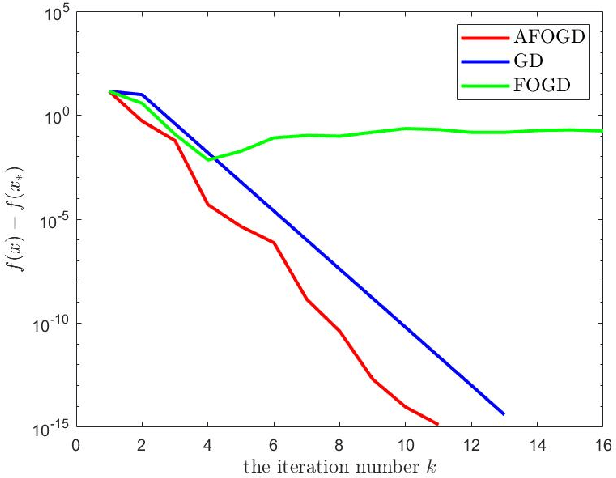
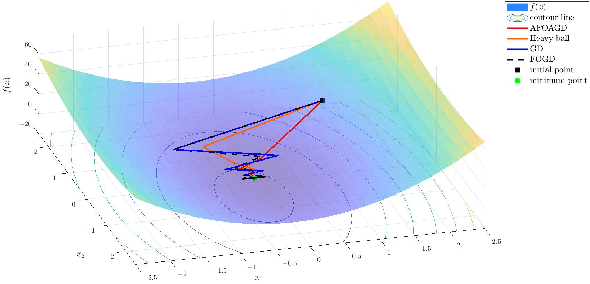
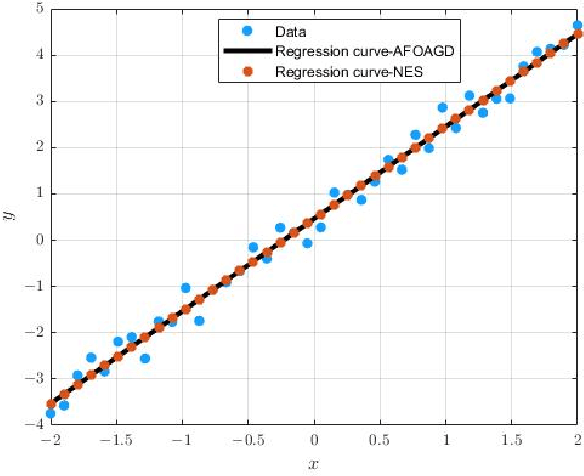
The vanilla fractional order gradient descent may oscillatively converge to a region around the global minimum instead of converging to the exact minimum point, or even diverge, in the case where the objective function is strongly convex. To address this problem, a novel adaptive fractional order gradient descent (AFOGD) method and a novel adaptive fractional order accelerated gradient descent (AFOAGD) method are proposed in this paper. Inspired by the quadratic constraints and Lyapunov stability analysis from robust control theory, we establish a linear matrix inequality to analyse the convergence of our proposed algorithms. We prove that the proposed algorithms can achieve R-linear convergence when the objective function is $\textbf{L-}$smooth and $\textbf{m-}$strongly-convex. Several numerical simulations are demonstrated to verify the effectiveness and superiority of our proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge