An AI-enabled tool for quantifying overlapping red blood cell sickling dynamics in microfluidic assays

Understanding sickle cell dynamics requires accurate identification of morphological transitions under diverse biophysical conditions, particularly in densely packed and overlapping cell populations. Here, we present an automated deep learning framework that integrates AI-assisted annotation, segmentation, classification, and instance counting to quantify red blood cell (RBC) populations across varying density regimes in time-lapse microscopy data. Experimental images were annotated using the Roboflow platform to generate labeled dataset for training an nnU-Net segmentation model. The trained network enables prediction of the temporal evolution of the sickle cell fraction, while a watershed algorithm resolves overlapping cells to enhance quantification accuracy. Despite requiring only a limited amount of labeled data for training, the framework achieves high segmentation performance, effectively addressing challenges associated with scarce manual annotations and cell overlap. By quantitatively tracking dynamic changes in RBC morphology, this approach can more than double the experimental throughput via densely packed cell suspensions, capture drug-dependent sickling behavior, and reveal distinct mechanobiological signatures of cellular morphological evolution. Overall, this AI-driven framework establishes a scalable and reproducible computational platform for investigating cellular biomechanics and assessing therapeutic efficacy in microphysiological systems.

SolARED: Solar Active Region Emergence Dataset for Machine Learning Aided Predictions

The development of accurate forecasts of solar eruptive activity has become increasingly important for preventing potential impacts on space technologies and exploration. Therefore, it is crucial to detect Active Regions (ARs) before they start forming on the solar surface. This will enable the development of early-warning capabilities for upcoming space weather disturbances. For this reason, we prepared the Solar Active Region Emergence Dataset (SolARED). The dataset is derived from full-disk maps of the Doppler velocity, magnetic field, and continuum intensity, obtained by the Helioseismic and Magnetic Imager (HMI) onboard the Solar Dynamics Observatory (SDO). SolARED includes time series of remapped, tracked, and binned data that characterize the evolution of acoustic power of solar oscillations, unsigned magnetic flux, and continuum intensity for 50 large ARs before, during, and after their emergence on the solar surface, as well as surrounding areas observed on the solar disc between 2010 and 2023. The resulting ML-ready SolARED dataset is designed to support enhancements of predictive capabilities, enabling the development of operational forecasts for the emergence of active regions. The SolARED dataset is available at https://sun.njit.edu/sarportal/, through an interactive visualization web application.

Forecasting Continuum Intensity for Solar Active Region Emergence Prediction using Transformers

Early and accurate prediction of solar active region (AR) emergence is crucial for space weather forecasting. Building on established Long Short-Term Memory (LSTM) based approaches for forecasting the continuum intensity decrease associated with AR emergence, this work expands the modeling with new architectures and targets. We investigate a sliding-window Transformer architecture to forecast continuum intensity evolution up to 12 hours ahead using data from 46 ARs observed by SDO/HMI. We conduct a systematic ablation study to evaluate two key components: (1) the inclusion of a temporal 1D convolutional (Conv1D) front-end and (2) a novel `Early Detection' architecture featuring attention biases and a timing-aware loss function. Our best-performing model, combining the Early Detection architecture without the Conv1D layer, achieved a Root Mean Square Error (RMSE) of 0.1189 (representing a 10.6% improvement over the LSTM baseline) and an average advance warning time of 4.73 hours (timing difference of -4.73h), even under a stricter emergence criterion than previous studies. While the Transformer demonstrates superior aggregate timing and accuracy, we note that this high-sensitivity detection comes with increased variance compared to smoother baseline models. However, this volatility is a necessary trade-off for operational warning systems: the model's ability to detect micro-changes in precursor signals enables significantly earlier detection, outweighing the cost of increased noise. Our results demonstrate that Transformer architectures modified with early detection biases, when used without temporal smoothing layers, provide a high-sensitivity alternative for forecasting AR emergence that prioritizes advance warning over statistical smoothness.

Arcee: Differentiable Recurrent State Chain for Generative Vision Modeling with Mamba SSMs

State-space models (SSMs), Mamba in particular, are increasingly adopted for long-context sequence modeling, providing linear-time aggregation via an input-dependent, causal selective-scan operation. Along this line, recent "Mamba-for-vision" variants largely explore multiple scan orders to relax strict causality for non-sequential signals (e.g., images). Rather than preserving cross-block memory, the conventional formulation of the selective-scan operation in Mamba reinitializes each block's state-space dynamics from zero, discarding the terminal state-space representation (SSR) from the previous block. Arcee, a cross-block recurrent state chain, reuses each block's terminal state-space representation as the initial condition for the next block. Handoff across blocks is constructed as a differentiable boundary map whose Jacobian enables end-to-end gradient flow across terminal boundaries. Key to practicality, Arcee is compatible with all prior "vision-mamba" variants, parameter-free, and incurs constant, negligible cost. As a modeling perspective, we view terminal SSR as a mild directional prior induced by a causal pass over the input, rather than an estimator of the non-sequential signal itself. To quantify the impact, for unconditional generation on CelebA-HQ (256$\times$256) with Flow Matching, Arcee reduces FID$\downarrow$ from $82.81$ to $15.33$ ($5.4\times$ lower) on a single scan-order Zigzag Mamba baseline. Efficient CUDA kernels and training code will be released to support rigorous and reproducible research.

BrainATCL: Adaptive Temporal Brain Connectivity Learning for Functional Link Prediction and Age Estimation

Functional Magnetic Resonance Imaging (fMRI) is an imaging technique widely used to study human brain activity. fMRI signals in areas across the brain transiently synchronise and desynchronise their activity in a highly structured manner, even when an individual is at rest. These functional connectivity dynamics may be related to behaviour and neuropsychiatric disease. To model these dynamics, temporal brain connectivity representations are essential, as they reflect evolving interactions between brain regions and provide insight into transient neural states and network reconfigurations. However, conventional graph neural networks (GNNs) often struggle to capture long-range temporal dependencies in dynamic fMRI data. To address this challenge, we propose BrainATCL, an unsupervised, nonparametric framework for adaptive temporal brain connectivity learning, enabling functional link prediction and age estimation. Our method dynamically adjusts the lookback window for each snapshot based on the rate of newly added edges. Graph sequences are subsequently encoded using a GINE-Mamba2 backbone to learn spatial-temporal representations of dynamic functional connectivity in resting-state fMRI data of 1,000 participants from the Human Connectome Project. To further improve spatial modeling, we incorporate brain structure and function-informed edge attributes, i.e., the left/right hemispheric identity and subnetwork membership of brain regions, enabling the model to capture biologically meaningful topological patterns. We evaluate our BrainATCL on two tasks: functional link prediction and age estimation. The experimental results demonstrate superior performance and strong generalization, including in cross-session prediction scenarios.

Hierarchical Mamba Meets Hyperbolic Geometry: A New Paradigm for Structured Language Embeddings

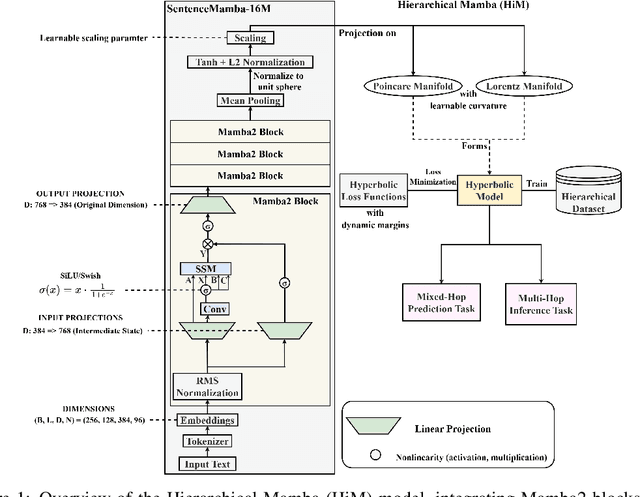
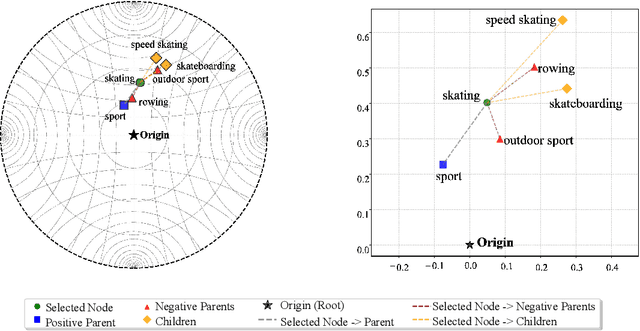
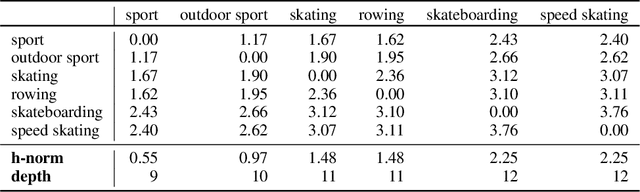
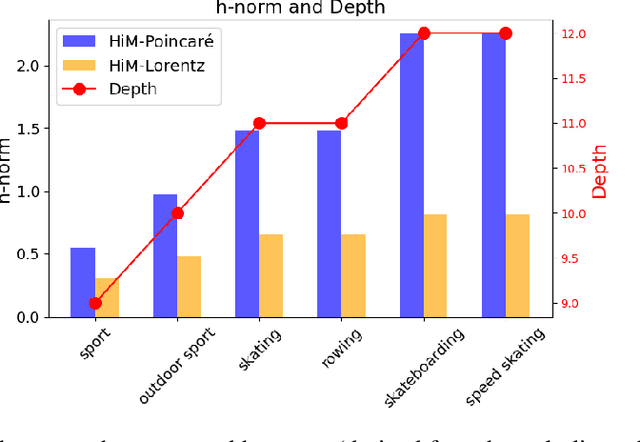
Selective state-space models have achieved great success in long-sequence modeling. However, their capacity for language representation, especially in complex hierarchical reasoning tasks, remains underexplored. Most large language models rely on flat Euclidean embeddings, limiting their ability to capture latent hierarchies. To address this limitation, we propose Hierarchical Mamba (HiM), integrating efficient Mamba2 with exponential growth and curved nature of hyperbolic geometry to learn hierarchy-aware language embeddings for deeper linguistic understanding. Mamba2-processed sequences are projected to the Poincare ball (via tangent-based mapping) or Lorentzian manifold (via cosine and sine-based mapping) with "learnable" curvature, optimized with a combined hyperbolic loss. Our HiM model facilitates the capture of relational distances across varying hierarchical levels, enabling effective long-range reasoning. This makes it well-suited for tasks like mixed-hop prediction and multi-hop inference in hierarchical classification. We evaluated our HiM with four linguistic and medical datasets for mixed-hop prediction and multi-hop inference tasks. Experimental results demonstrated that: 1) Both HiM models effectively capture hierarchical relationships for four ontological datasets, surpassing Euclidean baselines. 2) HiM-Poincare captures fine-grained semantic distinctions with higher h-norms, while HiM-Lorentz provides more stable, compact, and hierarchy-preserving embeddings favoring robustness over detail.

A Comparative Study on Dynamic Graph Embedding based on Mamba and Transformers

Dynamic graph embedding has emerged as an important technique for modeling complex time-evolving networks across diverse domains. While transformer-based models have shown promise in capturing long-range dependencies in temporal graph data, they face scalability challenges due to quadratic computational complexity. This study presents a comparative analysis of dynamic graph embedding approaches using transformers and the recently proposed Mamba architecture, a state-space model with linear complexity. We introduce three novel models: TransformerG2G augment with graph convolutional networks, DG-Mamba, and GDG-Mamba with graph isomorphism network edge convolutions. Our experiments on multiple benchmark datasets demonstrate that Mamba-based models achieve comparable or superior performance to transformer-based approaches in link prediction tasks while offering significant computational efficiency gains on longer sequences. Notably, DG-Mamba variants consistently outperform transformer-based models on datasets with high temporal variability, such as UCI, Bitcoin, and Reality Mining, while maintaining competitive performance on more stable graphs like SBM. We provide insights into the learned temporal dependencies through analysis of attention weights and state matrices, revealing the models' ability to capture complex temporal patterns. By effectively combining state-space models with graph neural networks, our work addresses key limitations of previous approaches and contributes to the growing body of research on efficient temporal graph representation learning. These findings offer promising directions for scaling dynamic graph embedding to larger, more complex real-world networks, potentially enabling new applications in areas such as social network analysis, financial modeling, and biological system dynamics.

TransformerG2G: Adaptive time-stepping for learning temporal graph embeddings using transformers

Dynamic graph embedding has emerged as a very effective technique for addressing diverse temporal graph analytic tasks (i.e., link prediction, node classification, recommender systems, anomaly detection, and graph generation) in various applications. Such temporal graphs exhibit heterogeneous transient dynamics, varying time intervals, and highly evolving node features throughout their evolution. Hence, incorporating long-range dependencies from the historical graph context plays a crucial role in accurately learning their temporal dynamics. In this paper, we develop a graph embedding model with uncertainty quantification, TransformerG2G, by exploiting the advanced transformer encoder to first learn intermediate node representations from its current state ($t$) and previous context (over timestamps [$t-1, t-l$], $l$ is the length of context). Moreover, we employ two projection layers to generate lower-dimensional multivariate Gaussian distributions as each node's latent embedding at timestamp $t$. We consider diverse benchmarks with varying levels of ``novelty" as measured by the TEA plots. Our experiments demonstrate that the proposed TransformerG2G model outperforms conventional multi-step methods and our prior work (DynG2G) in terms of both link prediction accuracy and computational efficiency, especially for high degree of novelty. Furthermore, the learned time-dependent attention weights across multiple graph snapshots reveal the development of an automatic adaptive time stepping enabled by the transformer. Importantly, by examining the attention weights, we can uncover temporal dependencies, identify influential elements, and gain insights into the complex interactions within the graph structure. For example, we identified a strong correlation between attention weights and node degree at the various stages of the graph topology evolution.

Norm-based Generalization Bounds for Compositionally Sparse Neural Networks

In this paper, we investigate the Rademacher complexity of deep sparse neural networks, where each neuron receives a small number of inputs. We prove generalization bounds for multilayered sparse ReLU neural networks, including convolutional neural networks. These bounds differ from previous ones, as they consider the norms of the convolutional filters instead of the norms of the associated Toeplitz matrices, independently of weight sharing between neurons. As we show theoretically, these bounds may be orders of magnitude better than standard norm-based generalization bounds and empirically, they are almost non-vacuous in estimating generalization in various simple classification problems. Taken together, these results suggest that compositional sparsity of the underlying target function is critical to the success of deep neural networks.

Scalable algorithms for physics-informed neural and graph networks

Physics-informed machine learning (PIML) has emerged as a promising new approach for simulating complex physical and biological systems that are governed by complex multiscale processes for which some data are also available. In some instances, the objective is to discover part of the hidden physics from the available data, and PIML has been shown to be particularly effective for such problems for which conventional methods may fail. Unlike commercial machine learning where training of deep neural networks requires big data, in PIML big data are not available. Instead, we can train such networks from additional information obtained by employing the physical laws and evaluating them at random points in the space-time domain. Such physics-informed machine learning integrates multimodality and multifidelity data with mathematical models, and implements them using neural networks or graph networks. Here, we review some of the prevailing trends in embedding physics into machine learning, using physics-informed neural networks (PINNs) based primarily on feed-forward neural networks and automatic differentiation. For more complex systems or systems of systems and unstructured data, graph neural networks (GNNs) present some distinct advantages, and here we review how physics-informed learning can be accomplished with GNNs based on graph exterior calculus to construct differential operators; we refer to these architectures as physics-informed graph networks (PIGNs). We present representative examples for both forward and inverse problems and discuss what advances are needed to scale up PINNs, PIGNs and more broadly GNNs for large-scale engineering problems.