Decimated Prony's Method for Stable Super-resolution

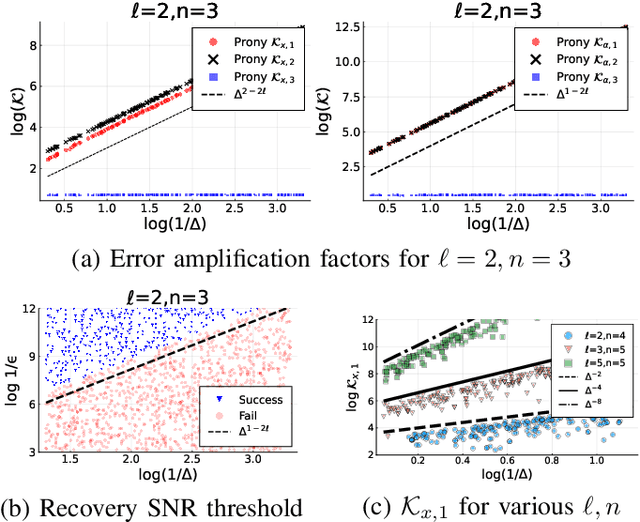
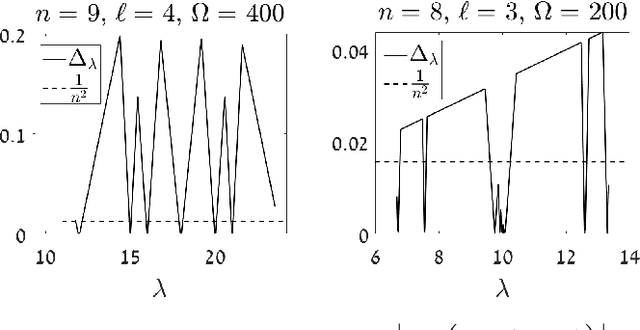
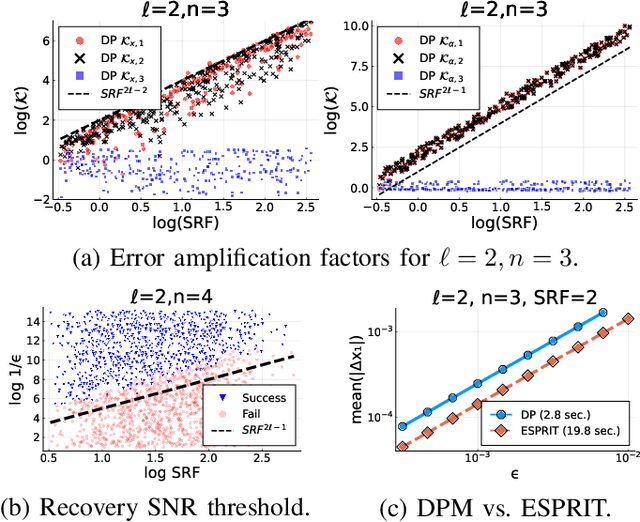
We study recovery of amplitudes and nodes of a finite impulse train from a limited number of equispaced noisy frequency samples. This problem is known as super-resolution (SR) under sparsity constraints and has numerous applications, including direction of arrival and finite rate of innovation sampling. Prony's method is an algebraic technique which fully recovers the signal parameters in the absence of measurement noise. In the presence of noise, Prony's method may experience significant loss of accuracy, especially when the separation between Dirac pulses is smaller than the Nyquist-Shannon-Rayleigh (NSR) limit. In this work we combine Prony's method with a recently established decimation technique for analyzing the SR problem in the regime where the distance between two or more pulses is much smaller than the NSR limit. We show that our approach attains optimal asymptotic stability in the presence of noise. Our result challenges the conventional belief that Prony-type methods tend to be highly numerically unstable.

A physically-informed Deep-Learning approach for locating sources in a waveguide

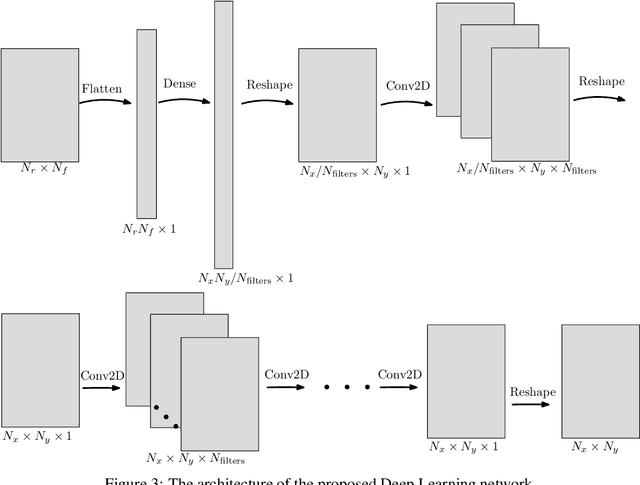
Inverse source problems are central to many applications in acoustics, geophysics, non-destructive testing, and more. Traditional imaging methods suffer from the resolution limit, preventing distinction of sources separated by less than the emitted wavelength. In this work we propose a method based on physically-informed neural-networks for solving the source refocusing problem, constructing a novel loss term which promotes super-resolving capabilities of the network and is based on the physics of wave propagation. We demonstrate the approach in the setup of imaging an a-priori unknown number of point sources in a two-dimensional rectangular waveguide from measurements of wavefield recordings along a vertical cross-section. The results show the ability of the method to approximate the locations of sources with high accuracy, even when placed close to each other.

On the Global-Local Dichotomy in Sparsity Modeling

The traditional sparse modeling approach, when applied to inverse problems with large data such as images, essentially assumes a sparse model for small overlapping data patches. While producing state-of-the-art results, this methodology is suboptimal, as it does not attempt to model the entire global signal in any meaningful way - a nontrivial task by itself. In this paper we propose a way to bridge this theoretical gap by constructing a global model from the bottom up. Given local sparsity assumptions in a dictionary, we show that the global signal representation must satisfy a constrained underdetermined system of linear equations, which can be solved efficiently by modern optimization methods such as Alternating Direction Method of Multipliers (ADMM). We investigate conditions for unique and stable recovery, and provide numerical evidence corroborating the theory.