Conformalized-KANs: Uncertainty Quantification with Coverage Guarantees for Kolmogorov-Arnold Networks (KANs) in Scientific Machine Learning
Paper and Code
Apr 21, 2025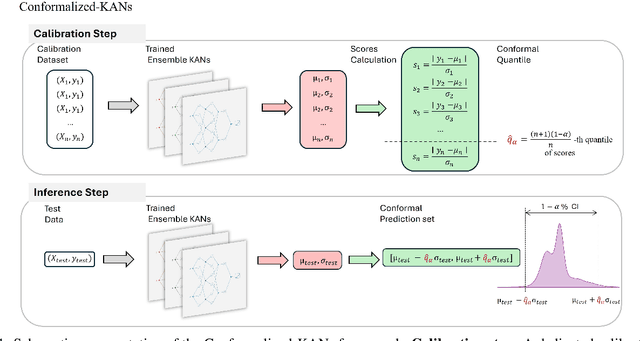

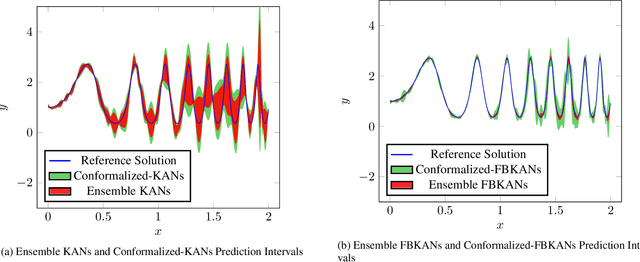

This paper explores uncertainty quantification (UQ) methods in the context of Kolmogorov-Arnold Networks (KANs). We apply an ensemble approach to KANs to obtain a heuristic measure of UQ, enhancing interpretability and robustness in modeling complex functions. Building on this, we introduce Conformalized-KANs, which integrate conformal prediction, a distribution-free UQ technique, with KAN ensembles to generate calibrated prediction intervals with guaranteed coverage. Extensive numerical experiments are conducted to evaluate the effectiveness of these methods, focusing particularly on the robustness and accuracy of the prediction intervals under various hyperparameter settings. We show that the conformal KAN predictions can be applied to recent extensions of KANs, including Finite Basis KANs (FBKANs) and multifideilty KANs (MFKANs). The results demonstrate the potential of our approaches to improve the reliability and applicability of KANs in scientific machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge