Linking Gaussian Process regression with data-driven manifold embeddings for nonlinear data fusion
Paper and Code
Dec 16, 2018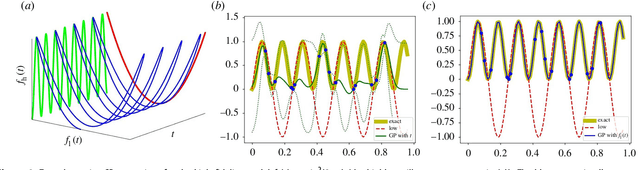
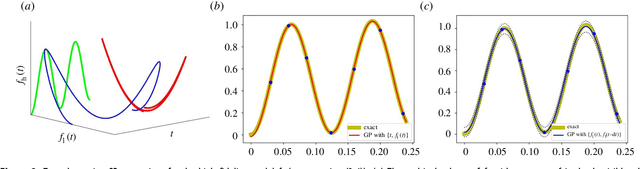
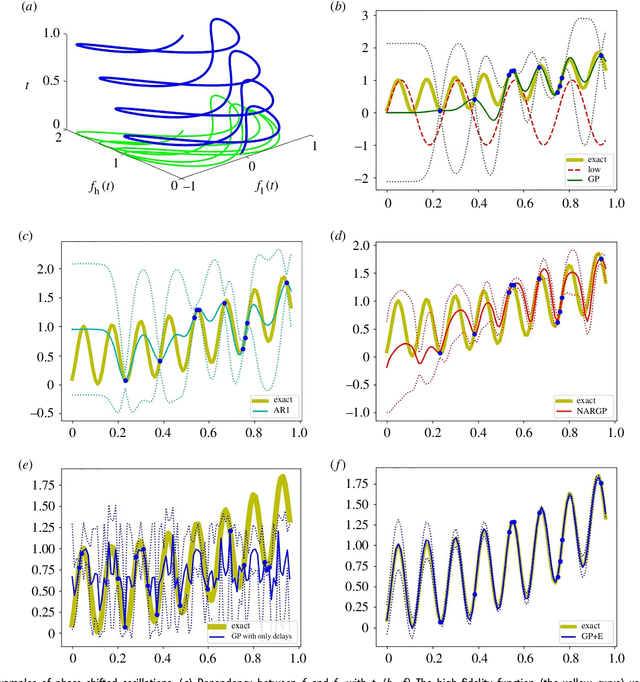
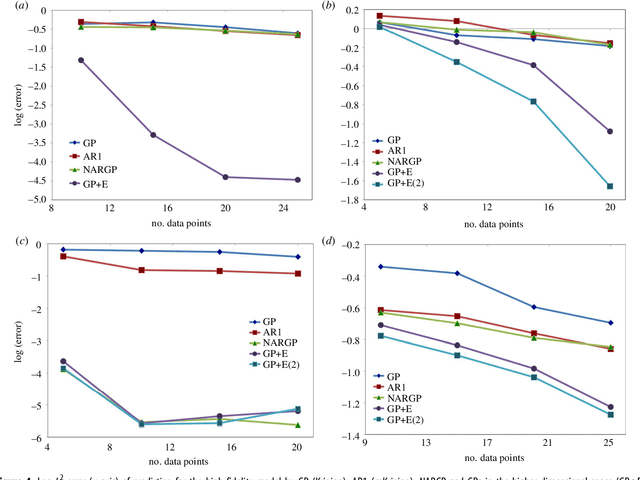
In statistical modeling with Gaussian Process regression, it has been shown that combining (few) high-fidelity data with (many) low-fidelity data can enhance prediction accuracy, compared to prediction based on the few high-fidelity data only. Such information fusion techniques for multifidelity data commonly approach the high-fidelity model $f_h(t)$ as a function of two variables $(t,y)$, and then using $f_l(t)$ as the $y$ data. More generally, the high-fidelity model can be written as a function of several variables $(t,y_1,y_2....)$; the low-fidelity model $f_l$ and, say, some of its derivatives, can then be substituted for these variables. In this paper, we will explore mathematical algorithms for multifidelity information fusion that use such an approach towards improving the representation of the high-fidelity function with only a few training data points. Given that $f_h$ may not be a simple function -- and sometimes not even a function -- of $f_l$, we demonstrate that using additional functions of $t$, such as derivatives or shifts of $f_l$, can drastically improve the approximation of $f_h$ through Gaussian Processes. We also point out a connection with "embedology" techniques from topology and dynamical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge