Michael Parks
nPINNs: nonlocal Physics-Informed Neural Networks for a parametrized nonlocal universal Laplacian operator. Algorithms and Applications
Apr 08, 2020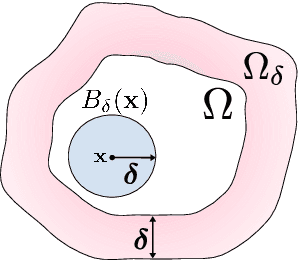
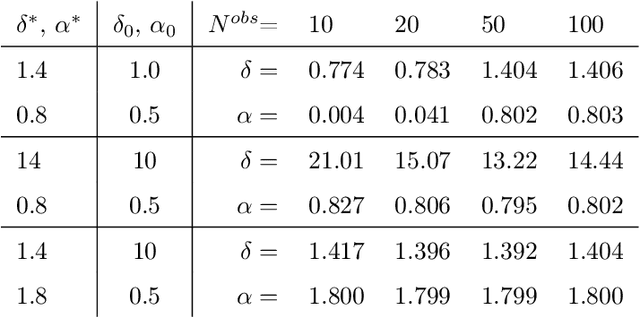
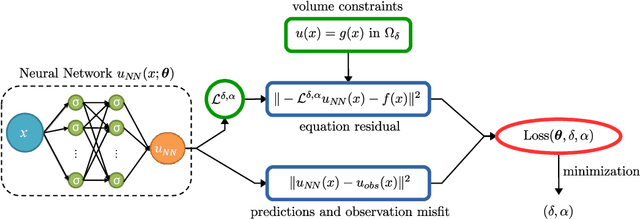
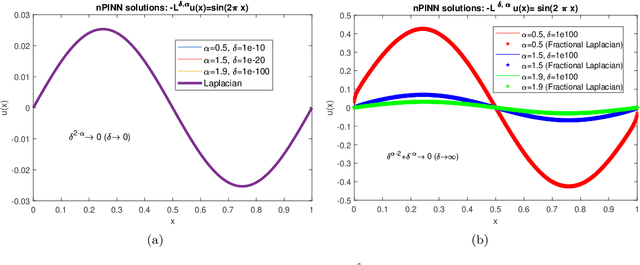
Abstract:Physics-informed neural networks (PINNs) are effective in solving inverse problems based on differential and integral equations with sparse, noisy, unstructured, and multi-fidelity data. PINNs incorporate all available information into a loss function, thus recasting the original problem into an optimization problem. In this paper, we extend PINNs to parameter and function inference for integral equations such as nonlocal Poisson and nonlocal turbulence models, and we refer to them as nonlocal PINNs (nPINNs). The contribution of the paper is three-fold. First, we propose a unified nonlocal operator, which converges to the classical Laplacian as one of the operator parameters, the nonlocal interaction radius $\delta$ goes to zero, and to the fractional Laplacian as $\delta$ goes to infinity. This universal operator forms a super-set of classical Laplacian and fractional Laplacian operators and, thus, has the potential to fit a broad spectrum of data sets. We provide theoretical convergence rates with respect to $\delta$ and verify them via numerical experiments. Second, we use nPINNs to estimate the two parameters, $\delta$ and $\alpha$. The strong non-convexity of the loss function yielding multiple (good) local minima reveals the occurrence of the operator mimicking phenomenon: different pairs of estimated parameters could produce multiple solutions of comparable accuracy. Third, we propose another nonlocal operator with spatially variable order $\alpha(y)$, which is more suitable for modeling turbulent Couette flow. Our results show that nPINNs can jointly infer this function as well as $\delta$. Also, these parameters exhibit a universal behavior with respect to the Reynolds number, a finding that contributes to our understanding of nonlocal interactions in wall-bounded turbulence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge