Active partitioning: inverting the paradigm of active learning

Datasets often incorporate various functional patterns related to different aspects or regimes, which are typically not equally present throughout the dataset. We propose a novel, general-purpose partitioning algorithm that utilizes competition between models to detect and separate these functional patterns. This competition is induced by multiple models iteratively submitting their predictions for the dataset, with the best prediction for each data point being rewarded with training on that data point. This reward mechanism amplifies each model's strengths and encourages specialization in different patterns. The specializations can then be translated into a partitioning scheme. The amplification of each model's strengths inverts the active learning paradigm: while active learning typically focuses the training of models on their weaknesses to minimize the number of required training data points, our concept reinforces the strengths of each model, thus specializing them. We validate our concept -- called active partitioning -- with various datasets with clearly distinct functional patterns, such as mechanical stress and strain data in a porous structure. The active partitioning algorithm produces valuable insights into the datasets' structure, which can serve various further applications. As a demonstration of one exemplary usage, we set up modular models consisting of multiple expert models, each learning a single partition, and compare their performance on more than twenty popular regression problems with single models learning all partitions simultaneously. Our results show significant improvements, with up to 54% loss reduction, confirming our partitioning algorithm's utility.

Automated Model Discovery for Tensional Homeostasis: Constitutive Machine Learning in Growth and Remodeling

Soft biological tissues exhibit a tendency to maintain a preferred state of tensile stress, known as tensional homeostasis, which is restored even after external mechanical stimuli. This macroscopic behavior can be described using the theory of kinematic growth, where the deformation gradient is multiplicatively decomposed into an elastic part and a part related to growth and remodeling. Recently, the concept of homeostatic surfaces was introduced to define the state of homeostasis and the evolution equations for inelastic deformations. However, identifying the optimal model and material parameters to accurately capture the macroscopic behavior of inelastic materials can only be accomplished with significant expertise, is often time-consuming, and prone to error, regardless of the specific inelastic phenomenon. To address this challenge, built-in physics machine learning algorithms offer significant potential. In this work, we extend our inelastic Constitutive Artificial Neural Networks (iCANNs) by incorporating kinematic growth and homeostatic surfaces to discover the scalar model equations, namely the Helmholtz free energy and the pseudo potential. The latter describes the state of homeostasis in a smeared sense. We evaluate the ability of the proposed network to learn from experimentally obtained tissue equivalent data at the material point level, assess its predictive accuracy beyond the training regime, and discuss its current limitations when applied at the structural level. Our source code, data, examples, and an implementation of the corresponding material subroutine are made accessible to the public at https://doi.org/10.5281/zenodo.13946282.

On sparse regression, Lp-regularization, and automated model discovery

Sparse regression and feature extraction are the cornerstones of knowledge discovery from massive data. Their goal is to discover interpretable and predictive models that provide simple relationships among scientific variables. While the statistical tools for model discovery are well established in the context of linear regression, their generalization to nonlinear regression in material modeling is highly problem-specific and insufficiently understood. Here we explore the potential of neural networks for automatic model discovery and induce sparsity by a hybrid approach that combines two strategies: regularization and physical constraints. We integrate the concept of Lp regularization for subset selection with constitutive neural networks that leverage our domain knowledge in kinematics and thermodynamics. We train our networks with both, synthetic and real data, and perform several thousand discovery runs to infer common guidelines and trends: L2 regularization or ridge regression is unsuitable for model discovery; L1 regularization or lasso promotes sparsity, but induces strong bias; only L0 regularization allows us to transparently fine-tune the trade-off between interpretability and predictability, simplicity and accuracy, and bias and variance. With these insights, we demonstrate that Lp regularized constitutive neural networks can simultaneously discover both, interpretable models and physically meaningful parameters. We anticipate that our findings will generalize to alternative discovery techniques such as sparse and symbolic regression, and to other domains such as biology, chemistry, or medicine. Our ability to automatically discover material models from data could have tremendous applications in generative material design and open new opportunities to manipulate matter, alter properties of existing materials, and discover new materials with user-defined properties.

Viscoelastic Constitutive Artificial Neural Networks (vCANNs) $-$ a framework for data-driven anisotropic nonlinear finite viscoelasticity

The constitutive behavior of polymeric materials is often modeled by finite linear viscoelastic (FLV) or quasi-linear viscoelastic (QLV) models. These popular models are simplifications that typically cannot accurately capture the nonlinear viscoelastic behavior of materials. For example, the success of attempts to capture strain rate-dependent behavior has been limited so far. To overcome this problem, we introduce viscoelastic Constitutive Artificial Neural Networks (vCANNs), a novel physics-informed machine learning framework for anisotropic nonlinear viscoelasticity at finite strains. vCANNs rely on the concept of generalized Maxwell models enhanced with nonlinear strain (rate)-dependent properties represented by neural networks. The flexibility of vCANNs enables them to automatically identify accurate and sparse constitutive models of a broad range of materials. To test vCANNs, we trained them on stress-strain data from Polyvinyl Butyral, the electro-active polymers VHB 4910 and 4905, and a biological tissue, the rectus abdominis muscle. Different loading conditions were considered, including relaxation tests, cyclic tension-compression tests, and blast loads. We demonstrate that vCANNs can learn to capture the behavior of all these materials accurately and computationally efficiently without human guidance.

Bayesian Physics-Informed Neural Networks for real-world nonlinear dynamical systems

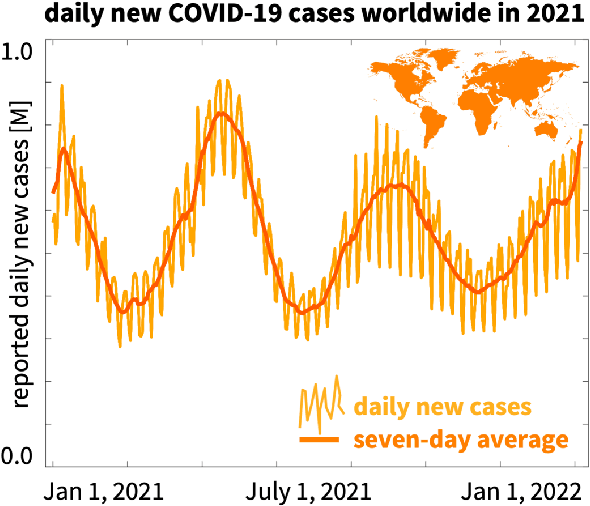
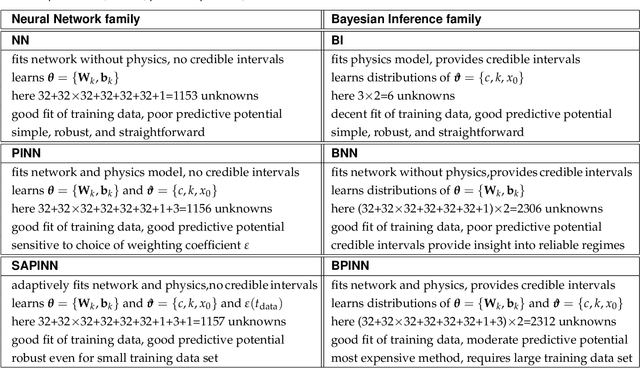
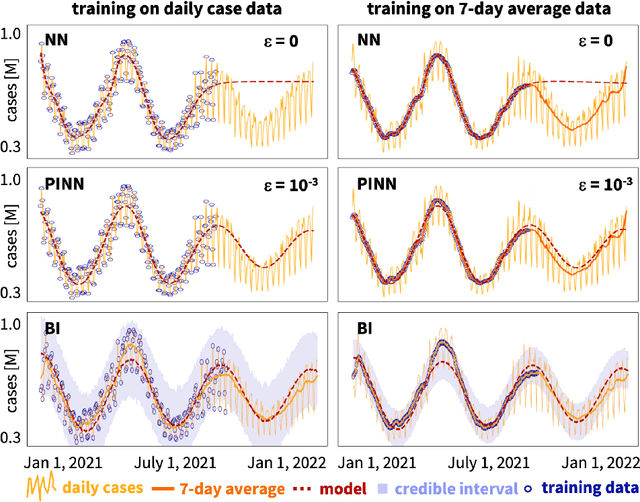
Understanding real-world dynamical phenomena remains a challenging task. Across various scientific disciplines, machine learning has advanced as the go-to technology to analyze nonlinear dynamical systems, identify patterns in big data, and make decision around them. Neural networks are now consistently used as universal function approximators for data with underlying mechanisms that are incompletely understood or exceedingly complex. However, neural networks alone ignore the fundamental laws of physics and often fail to make plausible predictions. Here we integrate data, physics, and uncertainties by combining neural networks, physics-informed modeling, and Bayesian inference to improve the predictive potential of traditional neural network models. We embed the physical model of a damped harmonic oscillator into a fully-connected feed-forward neural network to explore a simple and illustrative model system, the outbreak dynamics of COVID-19. Our Physics-Informed Neural Networks can seamlessly integrate data and physics, robustly solve forward and inverse problems, and perform well for both interpolation and extrapolation, even for a small amount of noisy and incomplete data. At only minor additional cost, they can self-adaptively learn the weighting between data and physics. Combined with Bayesian Neural Networks, they can serve as priors in a Bayesian Inference, and provide credible intervals for uncertainty quantification. Our study reveals the inherent advantages and disadvantages of Neural Networks, Bayesian Inference, and a combination of both and provides valuable guidelines for model selection. While we have only demonstrated these approaches for the simple model problem of a seasonal endemic infectious disease, we anticipate that the underlying concepts and trends generalize to more complex disease conditions and, more broadly, to a wide variety of nonlinear dynamical systems.