Automated Model Discovery for Tensional Homeostasis: Constitutive Machine Learning in Growth and Remodeling

Soft biological tissues exhibit a tendency to maintain a preferred state of tensile stress, known as tensional homeostasis, which is restored even after external mechanical stimuli. This macroscopic behavior can be described using the theory of kinematic growth, where the deformation gradient is multiplicatively decomposed into an elastic part and a part related to growth and remodeling. Recently, the concept of homeostatic surfaces was introduced to define the state of homeostasis and the evolution equations for inelastic deformations. However, identifying the optimal model and material parameters to accurately capture the macroscopic behavior of inelastic materials can only be accomplished with significant expertise, is often time-consuming, and prone to error, regardless of the specific inelastic phenomenon. To address this challenge, built-in physics machine learning algorithms offer significant potential. In this work, we extend our inelastic Constitutive Artificial Neural Networks (iCANNs) by incorporating kinematic growth and homeostatic surfaces to discover the scalar model equations, namely the Helmholtz free energy and the pseudo potential. The latter describes the state of homeostasis in a smeared sense. We evaluate the ability of the proposed network to learn from experimentally obtained tissue equivalent data at the material point level, assess its predictive accuracy beyond the training regime, and discuss its current limitations when applied at the structural level. Our source code, data, examples, and an implementation of the corresponding material subroutine are made accessible to the public at https://doi.org/10.5281/zenodo.13946282.

Theory and implementation of inelastic Constitutive Artificial Neural Networks

Nature has always been our inspiration in the research, design and development of materials and has driven us to gain a deep understanding of the mechanisms that characterize anisotropy and inelastic behavior. All this knowledge has been accumulated in the principles of thermodynamics. Deduced from these principles, the multiplicative decomposition combined with pseudo potentials are powerful and universal concepts. Simultaneously, the tremendous increase in computational performance enabled us to investigate and rethink our history-dependent material models to make the most of our predictions. Today, we have reached a point where materials and their models are becoming increasingly sophisticated. This raises the question: How do we find the best model that includes all inelastic effects to explain our complex data? Constitutive Artificial Neural Networks (CANN) may answer this question. Here, we extend the CANNs to inelastic materials (iCANN). Rigorous considerations of objectivity, rigid motion of the reference configuration, multiplicative decomposition and its inherent non-uniqueness, restrictions of energy and pseudo potential, and consistent evolution guide us towards the architecture of the iCANN satisfying thermodynamics per design. We combine feed-forward networks of the free energy and pseudo potential with a recurrent neural network approach to take time dependencies into account. We demonstrate that the iCANN is capable of autonomously discovering models for artificially generated data, the response of polymers for cyclic loading and the relaxation behavior of muscle data. As the design of the network is not limited to visco-elasticity, our vision is that the iCANN will reveal to us new ways to find the various inelastic phenomena hidden in the data and to understand their interaction. Our source code, data, and examples are available at doi.org/10.5281/zenodo.10066805

On sparse regression, Lp-regularization, and automated model discovery

Sparse regression and feature extraction are the cornerstones of knowledge discovery from massive data. Their goal is to discover interpretable and predictive models that provide simple relationships among scientific variables. While the statistical tools for model discovery are well established in the context of linear regression, their generalization to nonlinear regression in material modeling is highly problem-specific and insufficiently understood. Here we explore the potential of neural networks for automatic model discovery and induce sparsity by a hybrid approach that combines two strategies: regularization and physical constraints. We integrate the concept of Lp regularization for subset selection with constitutive neural networks that leverage our domain knowledge in kinematics and thermodynamics. We train our networks with both, synthetic and real data, and perform several thousand discovery runs to infer common guidelines and trends: L2 regularization or ridge regression is unsuitable for model discovery; L1 regularization or lasso promotes sparsity, but induces strong bias; only L0 regularization allows us to transparently fine-tune the trade-off between interpretability and predictability, simplicity and accuracy, and bias and variance. With these insights, we demonstrate that Lp regularized constitutive neural networks can simultaneously discover both, interpretable models and physically meaningful parameters. We anticipate that our findings will generalize to alternative discovery techniques such as sparse and symbolic regression, and to other domains such as biology, chemistry, or medicine. Our ability to automatically discover material models from data could have tremendous applications in generative material design and open new opportunities to manipulate matter, alter properties of existing materials, and discover new materials with user-defined properties.

Discovering a reaction-diffusion model for Alzheimer's disease by combining PINNs with symbolic regression

Misfolded tau proteins play a critical role in the progression and pathology of Alzheimer's disease. Recent studies suggest that the spatio-temporal pattern of misfolded tau follows a reaction-diffusion type equation. However, the precise mathematical model and parameters that characterize the progression of misfolded protein across the brain remain incompletely understood. Here, we use deep learning and artificial intelligence to discover a mathematical model for the progression of Alzheimer's disease using longitudinal tau positron emission tomography from the Alzheimer's Disease Neuroimaging Initiative database. Specifically, we integrate physics informed neural networks (PINNs) and symbolic regression to discover a reaction-diffusion type partial differential equation for tau protein misfolding and spreading. First, we demonstrate the potential of our model and parameter discovery on synthetic data. Then, we apply our method to discover the best model and parameters to explain tau imaging data from 46 individuals who are likely to develop Alzheimer's disease and 30 healthy controls. Our symbolic regression discovers different misfolding models $f(c)$ for two groups, with a faster misfolding for the Alzheimer's group, $f(c) = 0.23c^3 - 1.34c^2 + 1.11c$, than for the healthy control group, $f(c) = -c^3 +0.62c^2 + 0.39c$. Our results suggest that PINNs, supplemented by symbolic regression, can discover a reaction-diffusion type model to explain misfolded tau protein concentrations in Alzheimer's disease. We expect our study to be the starting point for a more holistic analysis to provide image-based technologies for early diagnosis, and ideally early treatment of neurodegeneration in Alzheimer's disease and possibly other misfolding-protein based neurodegenerative disorders.

Physics-guided deep learning for data scarcity

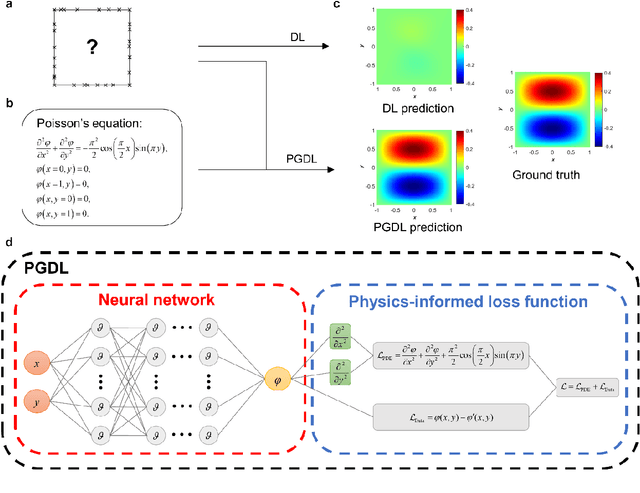
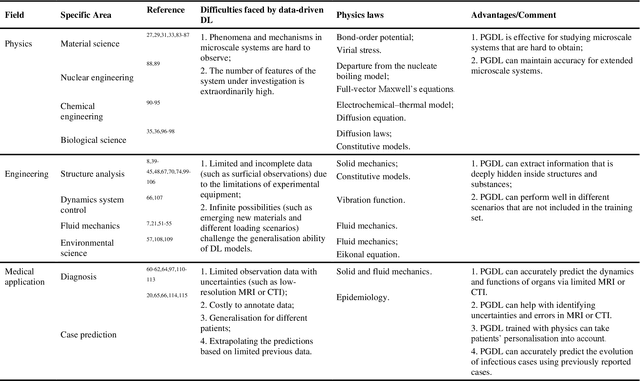
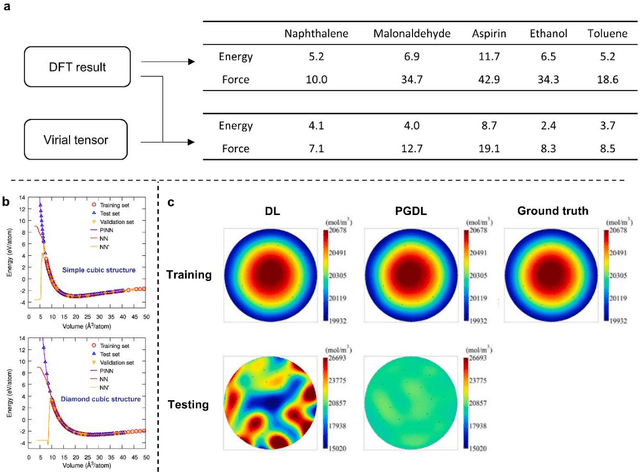
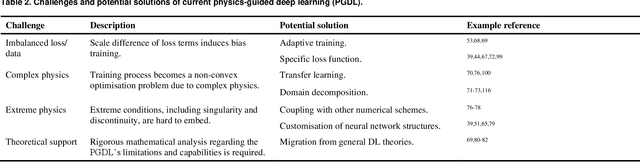
Data are the core of deep learning (DL), and the quality of data significantly affects the performance of DL models. However, high-quality and well-annotated databases are hard or even impossible to acquire for use in many applications, such as structural risk estimation and medical diagnosis, which is an essential barrier that blocks the applications of DL in real life. Physics-guided deep learning (PGDL) is a novel type of DL that can integrate physics laws to train neural networks. It can be used for any systems that are controlled or governed by physics laws, such as mechanics, finance and medical applications. It has been shown that, with the additional information provided by physics laws, PGDL achieves great accuracy and generalisation when facing data scarcity. In this review, the details of PGDL are elucidated, and a structured overview of PGDL with respect to data scarcity in various applications is presented, including physics, engineering and medical applications. Moreover, the limitations and opportunities for current PGDL in terms of data scarcity are identified, and the future outlook for PGDL is discussed in depth.

Bayesian Physics-Informed Neural Networks for real-world nonlinear dynamical systems

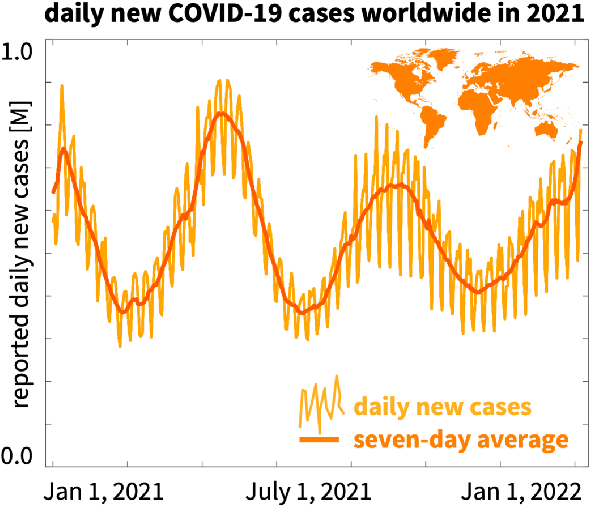
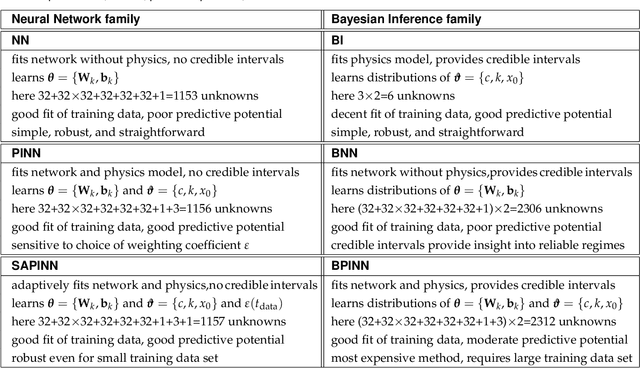
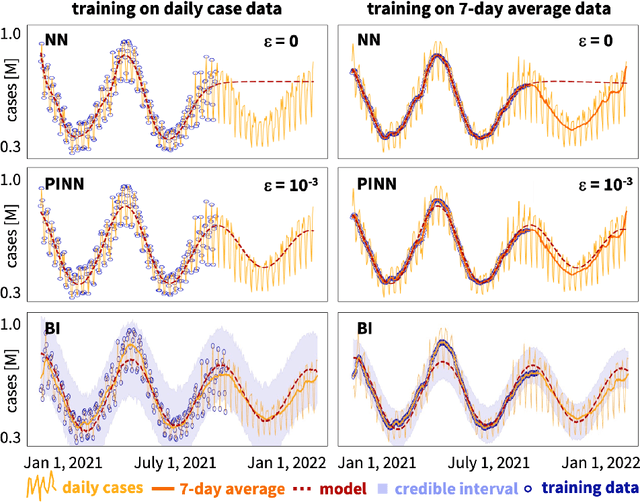
Understanding real-world dynamical phenomena remains a challenging task. Across various scientific disciplines, machine learning has advanced as the go-to technology to analyze nonlinear dynamical systems, identify patterns in big data, and make decision around them. Neural networks are now consistently used as universal function approximators for data with underlying mechanisms that are incompletely understood or exceedingly complex. However, neural networks alone ignore the fundamental laws of physics and often fail to make plausible predictions. Here we integrate data, physics, and uncertainties by combining neural networks, physics-informed modeling, and Bayesian inference to improve the predictive potential of traditional neural network models. We embed the physical model of a damped harmonic oscillator into a fully-connected feed-forward neural network to explore a simple and illustrative model system, the outbreak dynamics of COVID-19. Our Physics-Informed Neural Networks can seamlessly integrate data and physics, robustly solve forward and inverse problems, and perform well for both interpolation and extrapolation, even for a small amount of noisy and incomplete data. At only minor additional cost, they can self-adaptively learn the weighting between data and physics. Combined with Bayesian Neural Networks, they can serve as priors in a Bayesian Inference, and provide credible intervals for uncertainty quantification. Our study reveals the inherent advantages and disadvantages of Neural Networks, Bayesian Inference, and a combination of both and provides valuable guidelines for model selection. While we have only demonstrated these approaches for the simple model problem of a seasonal endemic infectious disease, we anticipate that the underlying concepts and trends generalize to more complex disease conditions and, more broadly, to a wide variety of nonlinear dynamical systems.

Multi-fidelity classification using Gaussian processes: accelerating the prediction of large-scale computational models

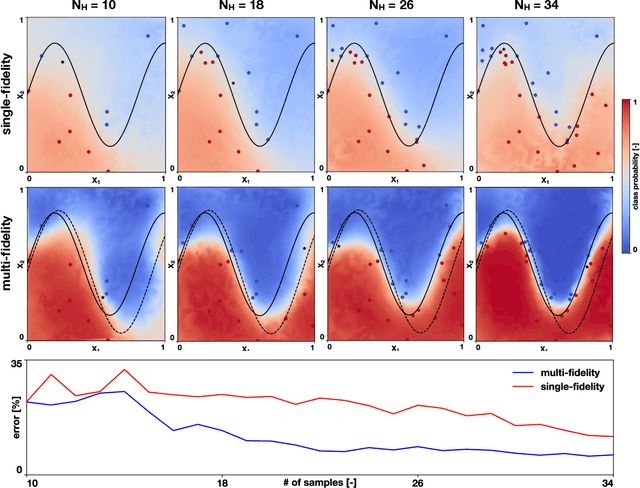
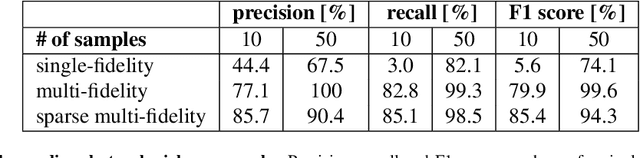
Machine learning techniques typically rely on large datasets to create accurate classifiers. However, there are situations when data is scarce and expensive to acquire. This is the case of studies that rely on state-of-the-art computational models which typically take days to run, thus hindering the potential of machine learning tools. In this work, we present a novel classifier that takes advantage of lower fidelity models and inexpensive approximations to predict the binary output of expensive computer simulations. We postulate an autoregressive model between the different levels of fidelity with Gaussian process priors. We adopt a fully Bayesian treatment for the hyper-parameters and use Markov Chain Mont Carlo samplers. We take advantage of the probabilistic nature of the classifier to implement active learning strategies. We also introduce a sparse approximation to enhance the ability of themulti-fidelity classifier to handle large datasets. We test these multi-fidelity classifiers against their single-fidelity counterpart with synthetic data, showing a median computational cost reduction of 23% for a target accuracy of 90%. In an application to cardiac electrophysiology, the multi-fidelity classifier achieves an F1 score, the harmonic mean of precision and recall, of 99.6% compared to 74.1% of a single-fidelity classifier when both are trained with 50 samples. In general, our results show that the multi-fidelity classifiers outperform their single-fidelity counterpart in terms of accuracy in all cases. We envision that this new tool will enable researchers to study classification problems that would otherwise be prohibitively expensive. Source code is available at https://github.com/fsahli/MFclass.