Energy-based physics-informed neural network for frictionless contact problems under large deformation

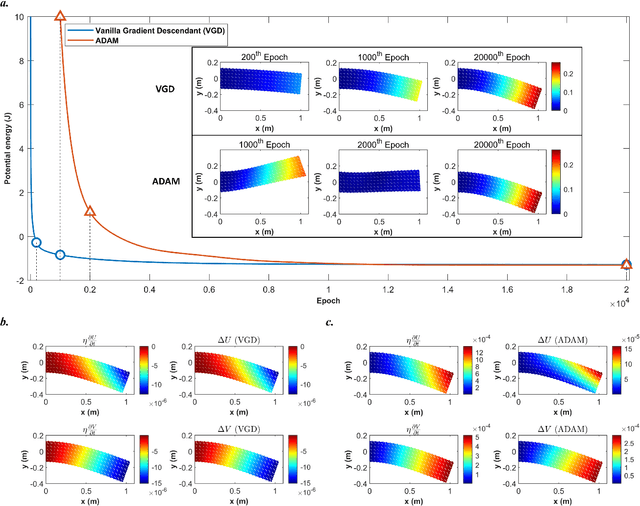
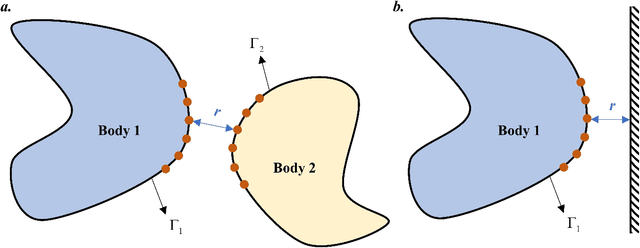
Numerical methods for contact mechanics are of great importance in engineering applications, enabling the prediction and analysis of complex surface interactions under various conditions. In this work, we propose an energy-based physics-informed neural network (PINNs) framework for solving frictionless contact problems under large deformation. Inspired by microscopic Lennard-Jones potential, a surface contact energy is used to describe the contact phenomena. To ensure the robustness of the proposed PINN framework, relaxation, gradual loading and output scaling techniques are introduced. In the numerical examples, the well-known Hertz contact benchmark problem is conducted, demonstrating the effectiveness and robustness of the proposed PINNs framework. Moreover, challenging contact problems with the consideration of geometrical and material nonlinearities are tested. It has been shown that the proposed PINNs framework provides a reliable and powerful tool for nonlinear contact mechanics. More importantly, the proposed PINNs framework exhibits competitive computational efficiency to the commercial FEM software when dealing with those complex contact problems. The codes used in this manuscript are available at https://github.com/JinshuaiBai/energy_PINN_Contact.(The code will be available after acceptance)

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov Arnold Networks

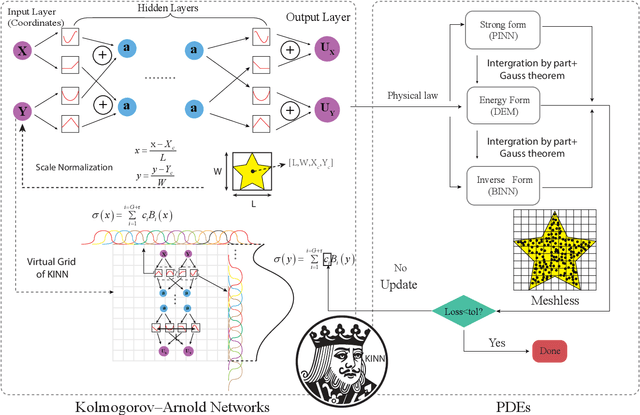
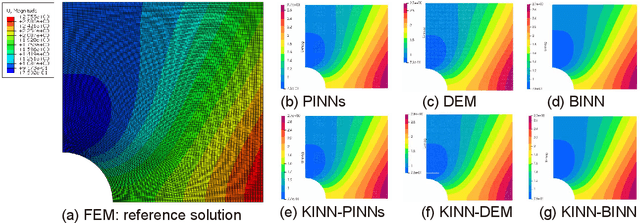
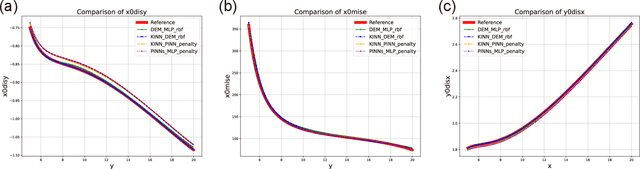
AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN). We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP in terms of accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN's potential for more efficient and accurate PDE solutions in AI for PDEs.

Physics-informed radial basis network : A local approximating neural network for solving nonlinear PDEs

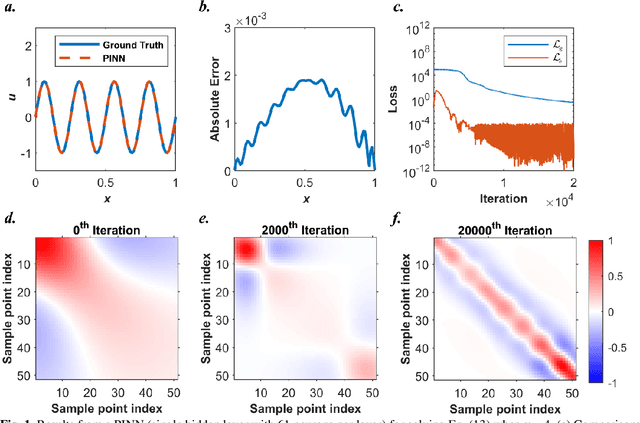
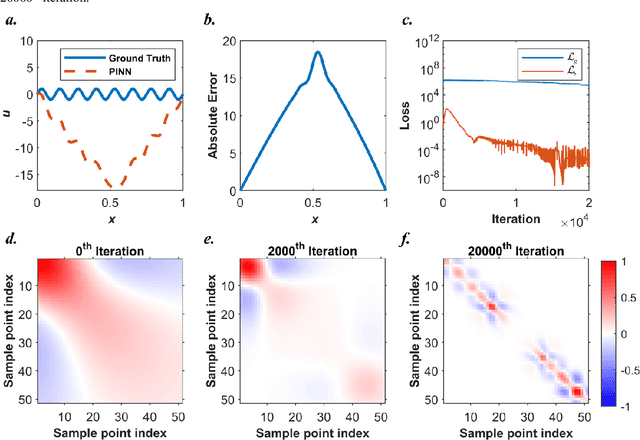
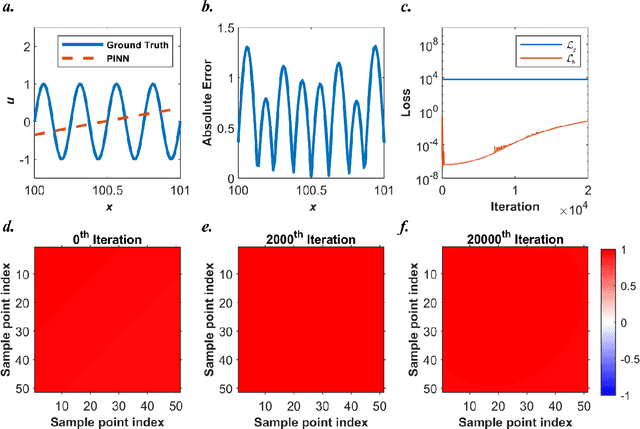
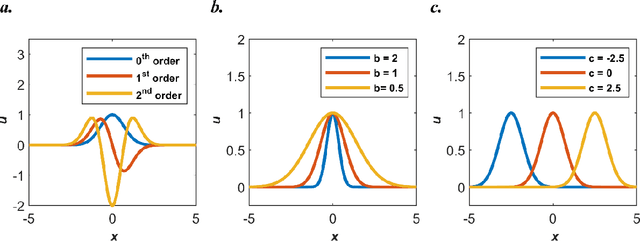
Our recent intensive study has found that physics-informed neural networks (PINN) tend to be local approximators after training. This observation leads to this novel physics-informed radial basis network (PIRBN), which can maintain the local property throughout the entire training process. Compared to deep neural networks, a PIRBN comprises of only one hidden layer and a radial basis "activation" function. Under appropriate conditions, we demonstrated that the training of PIRBNs using gradient descendent methods can converge to Gaussian processes. Besides, we studied the training dynamics of PIRBN via the neural tangent kernel (NTK) theory. In addition, comprehensive investigations regarding the initialisation strategies of PIRBN were conducted. Based on numerical examples, PIRBN has been demonstrated to be more effective and efficient than PINN in solving PDEs with high-frequency features and ill-posed computational domains. Moreover, the existing PINN numerical techniques, such as adaptive learning, decomposition and different types of loss functions, are applicable to PIRBN. The programs that can regenerate all numerical results can be found at https://github.com/JinshuaiBai/PIRBN.

Physics-guided deep learning for data scarcity

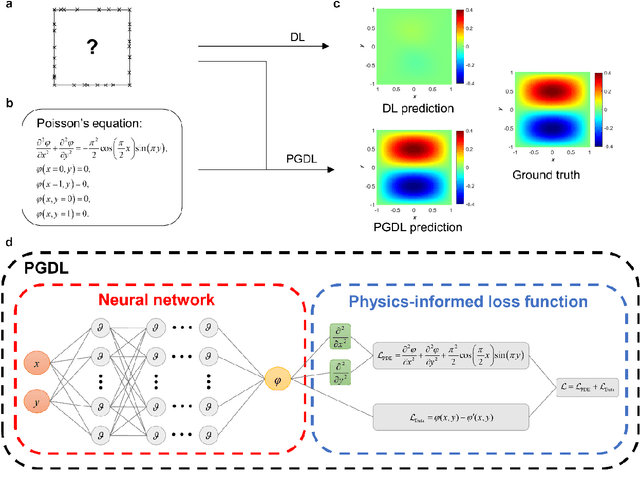
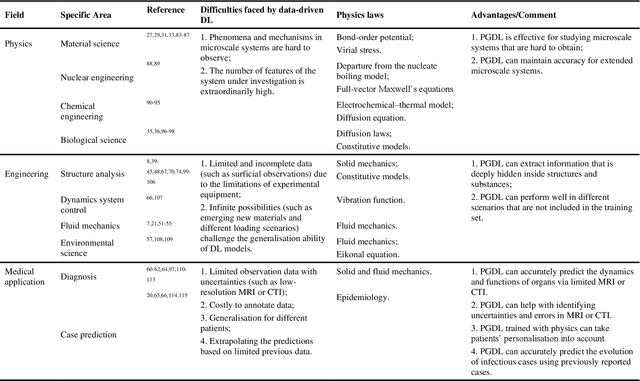
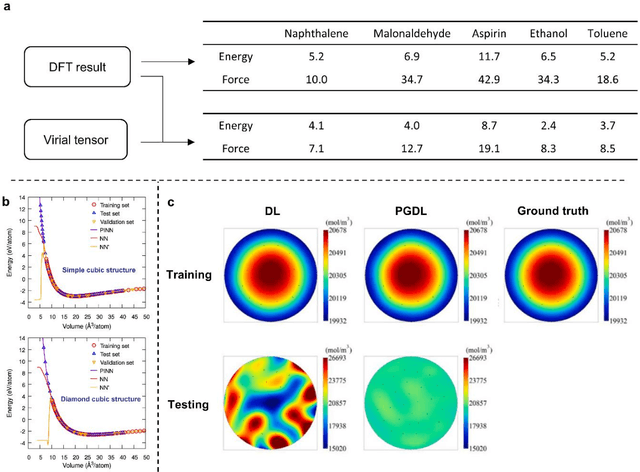
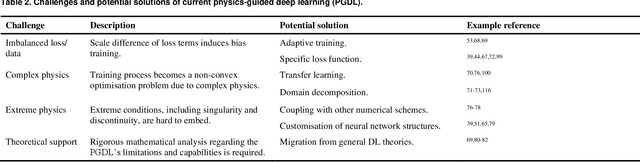
Data are the core of deep learning (DL), and the quality of data significantly affects the performance of DL models. However, high-quality and well-annotated databases are hard or even impossible to acquire for use in many applications, such as structural risk estimation and medical diagnosis, which is an essential barrier that blocks the applications of DL in real life. Physics-guided deep learning (PGDL) is a novel type of DL that can integrate physics laws to train neural networks. It can be used for any systems that are controlled or governed by physics laws, such as mechanics, finance and medical applications. It has been shown that, with the additional information provided by physics laws, PGDL achieves great accuracy and generalisation when facing data scarcity. In this review, the details of PGDL are elucidated, and a structured overview of PGDL with respect to data scarcity in various applications is presented, including physics, engineering and medical applications. Moreover, the limitations and opportunities for current PGDL in terms of data scarcity are identified, and the future outlook for PGDL is discussed in depth.