HAMNO: A Hierarchical Adaptive Multi-scale Neural Operator with Physics-Informed Learning for Dynamical Systems

Neural operators provide a powerful framework for learning solution mappings of partial differential equations directly in function space. However, many existing architectures still struggle to represent nonlinear time-dependent systems that involve multi-scale structures, long-range interactions, and stable long-time evolution. In this work, we introduce the Hierarchical Adaptive Multi-scale Neural Operator (HAMNO), a neural-operator architecture that combines local convolutional representations, global spectral operators, and hierarchical encoder-decoder processing. The central component of HAMNO is a data-dependent gating mechanism that adaptively balances local and global information at each spatial location, allowing the model to resolve fine-scale features while preserving long-range dependencies. We further develop a physics-informed extension, PI-HAMNO, based on a multi-objective loss strategy that combines data fitting with strong- and weak-form physics constraints. The strong-form term penalizes the domain-integrated squared PDE residual in physical coordinates, while the weak-form term is constructed by multiplying the governing residual by finite-element test functions and evaluating the resulting element integrals using centroid-based tetrahedral quadrature. The framework is evaluated on non-periodic Allen-Cahn (AC), Cahn-Hilliard (CH), and Swift-Hohenberg (SH) equations defined on cubic domains. Across long-horizon rollout, data-limited training, out-of-distribution initial-condition shifts, and random-seed variations, HAMNO improves predictive accuracy over standard neural-operator baselines, while PI-HAMNO further enhances stability, physical consistency, and data efficiency. The implementation is publicly available at https://github.com/MBamdad/HAMNO .

Replay-Based Continual Learning for Physics-Informed Neural Operators

Neural operators generally demonstrate strong predictive performance on in-distribution (ID) problems. However, a critical limitation of existing methods is their significant performance degradation when encountering out-of-distribution (OOD) data. To address this issue, this work introduces continual learning into physics-informed neural operators, with particular emphasis on neural operators built upon the Transolver architecture, and proposes a simple yet effective replay-based continual learning strategy. The proposed method is fully physics-informed and does not require labeled data, relying solely on input fields together with physical constraints for training. When new OOD data become available, a small number of past data are incorporated through a distillation-based constraint to preserve previously acquired knowledge and alleviate catastrophic forgetting. Meanwhile, a transfer learning LoRA is employed to enable rapid adaptation to the new data. The proposed framework is systematically validated on three representative physical problems, including the Darcy flow problem in fluid mechanics, a two-dimensional hyperelastic brain tumor problem in biomechanics, and a three-dimensional linear elastic Triply Periodic Minimal Surfaces problem in solid mechanics. The results demonstrate that the proposed method effectively mitigates catastrophic forgetting on previously learned data while maintaining fast adaptability to new data. Compared with conventional joint training strategies, the proposed method significantly improves training efficiency while reducing additional memory usage and computational cost.

Transfer Learning in Physics-Informed Neural Networks: Full Fine-Tuning, Lightweight Fine-Tuning, and Low-Rank Adaptation

AI for PDEs has garnered significant attention, particularly Physics-Informed Neural Networks (PINNs). However, PINNs are typically limited to solving specific problems, and any changes in problem conditions necessitate retraining. Therefore, we explore the generalization capability of transfer learning in the strong and energy form of PINNs across different boundary conditions, materials, and geometries. The transfer learning methods we employ include full finetuning, lightweight finetuning, and Low-Rank Adaptation (LoRA). The results demonstrate that full finetuning and LoRA can significantly improve convergence speed while providing a slight enhancement in accuracy.

DeepNetBeam: A Framework for the Analysis of Functionally Graded Porous Beams

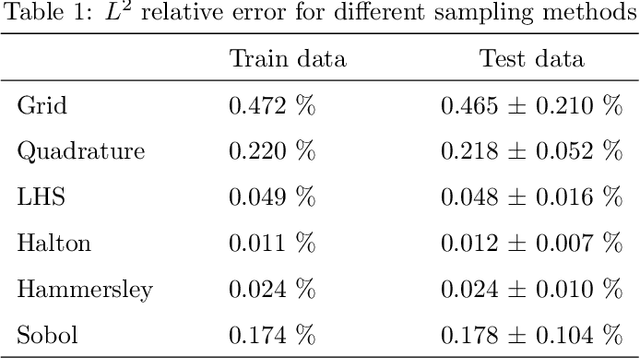
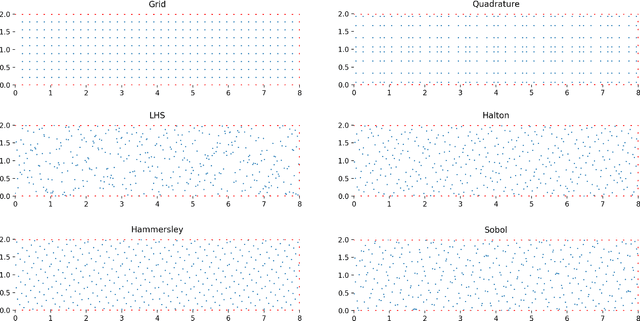
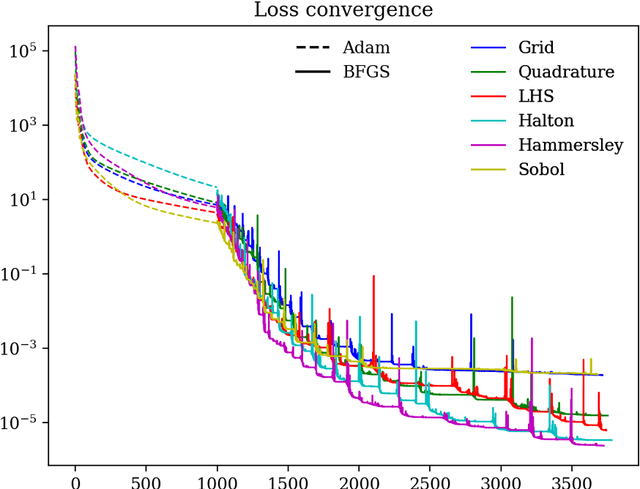
This study investigates different Scientific Machine Learning (SciML) approaches for the analysis of functionally graded (FG) porous beams and compares them under a new framework. The beam material properties are assumed to vary as an arbitrary continuous function. The methods consider the output of a neural network/operator as an approximation to the displacement fields and derive the equations governing beam behavior based on the continuum formulation. The methods are implemented in the framework and formulated by three approaches: (a) the vector approach leads to a Physics-Informed Neural Network (PINN), (b) the energy approach brings about the Deep Energy Method (DEM), and (c) the data-driven approach, which results in a class of Neural Operator methods. Finally, a neural operator has been trained to predict the response of the porous beam with functionally graded material under any porosity distribution pattern and any arbitrary traction condition. The results are validated with analytical and numerical reference solutions. The data and code accompanying this manuscript will be publicly available at https://github.com/eshaghi-ms/DeepNetBeam.

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov Arnold Networks

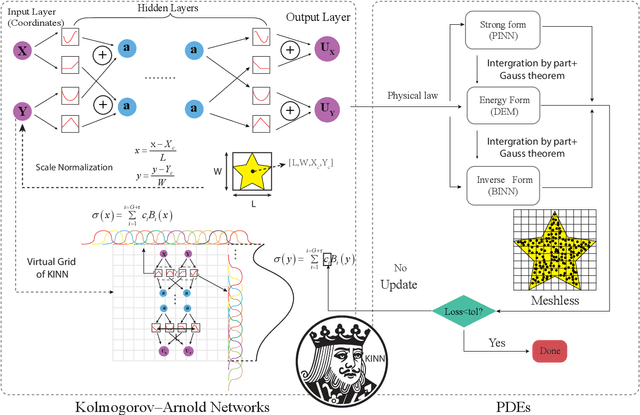
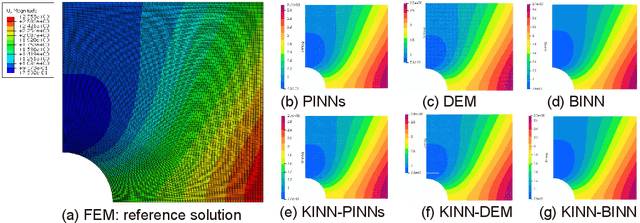
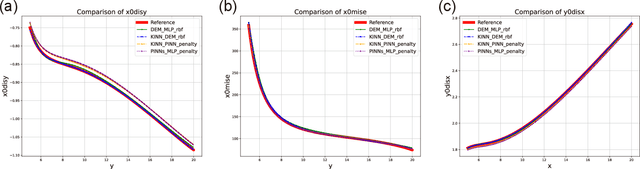
AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN). We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP in terms of accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN's potential for more efficient and accurate PDE solutions in AI for PDEs.