DeepNetBeam: A Framework for the Analysis of Functionally Graded Porous Beams

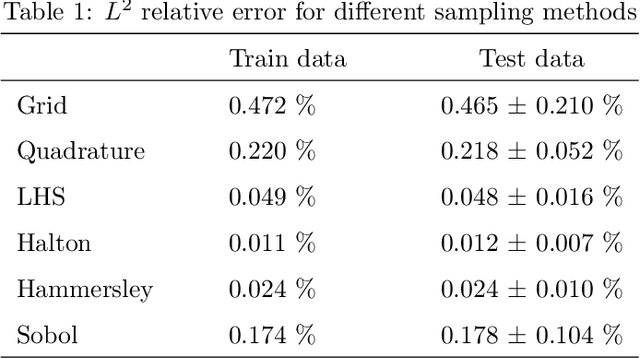
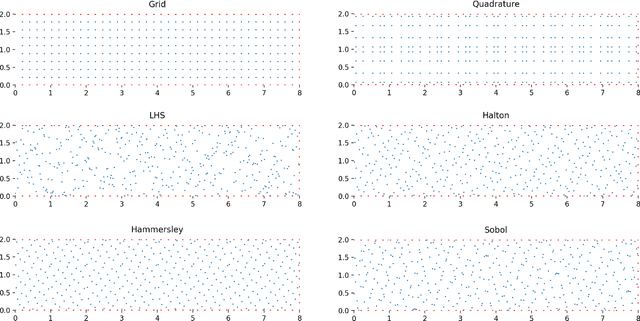
This study investigates different Scientific Machine Learning (SciML) approaches for the analysis of functionally graded (FG) porous beams and compares them under a new framework. The beam material properties are assumed to vary as an arbitrary continuous function. The methods consider the output of a neural network/operator as an approximation to the displacement fields and derive the equations governing beam behavior based on the continuum formulation. The methods are implemented in the framework and formulated by three approaches: (a) the vector approach leads to a Physics-Informed Neural Network (PINN), (b) the energy approach brings about the Deep Energy Method (DEM), and (c) the data-driven approach, which results in a class of Neural Operator methods. Finally, a neural operator has been trained to predict the response of the porous beam with functionally graded material under any porosity distribution pattern and any arbitrary traction condition. The results are validated with analytical and numerical reference solutions. The data and code accompanying this manuscript will be publicly available at https://github.com/eshaghi-ms/DeepNetBeam.

Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving PDEs based on Kolmogorov Arnold Networks

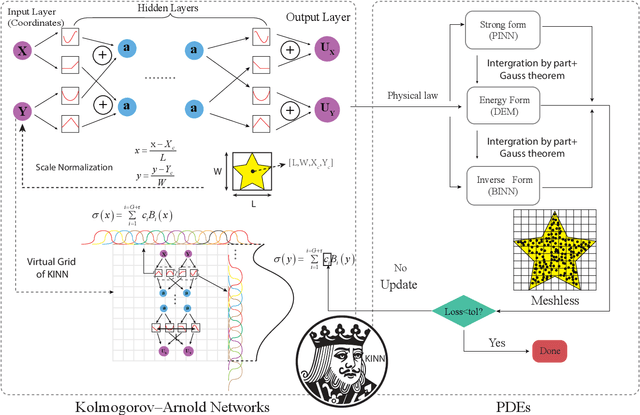
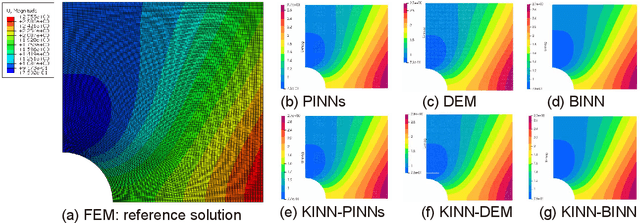
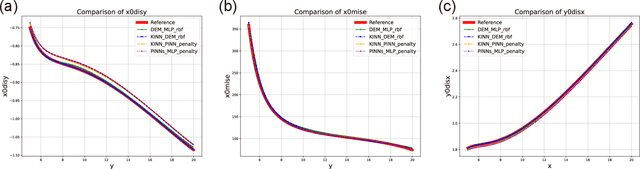
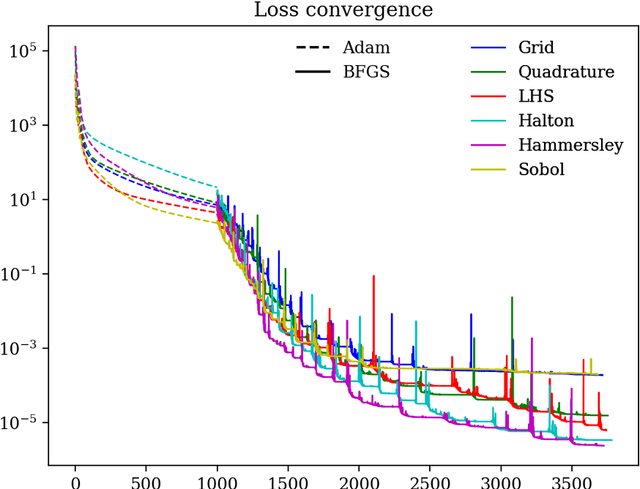
AI for partial differential equations (PDEs) has garnered significant attention, particularly with the emergence of Physics-informed neural networks (PINNs). The recent advent of Kolmogorov-Arnold Network (KAN) indicates that there is potential to revisit and enhance the previously MLP-based PINNs. Compared to MLPs, KANs offer interpretability and require fewer parameters. PDEs can be described in various forms, such as strong form, energy form, and inverse form. While mathematically equivalent, these forms are not computationally equivalent, making the exploration of different PDE formulations significant in computational physics. Thus, we propose different PDE forms based on KAN instead of MLP, termed Kolmogorov-Arnold-Informed Neural Network (KINN). We systematically compare MLP and KAN in various numerical examples of PDEs, including multi-scale, singularity, stress concentration, nonlinear hyperelasticity, heterogeneous, and complex geometry problems. Our results demonstrate that KINN significantly outperforms MLP in terms of accuracy and convergence speed for numerous PDEs in computational solid mechanics, except for the complex geometry problem. This highlights KINN's potential for more efficient and accurate PDE solutions in AI for PDEs.

An Energy Approach to the Solution of Partial Differential Equations in Computational Mechanics via Machine Learning: Concepts, Implementation and Applications

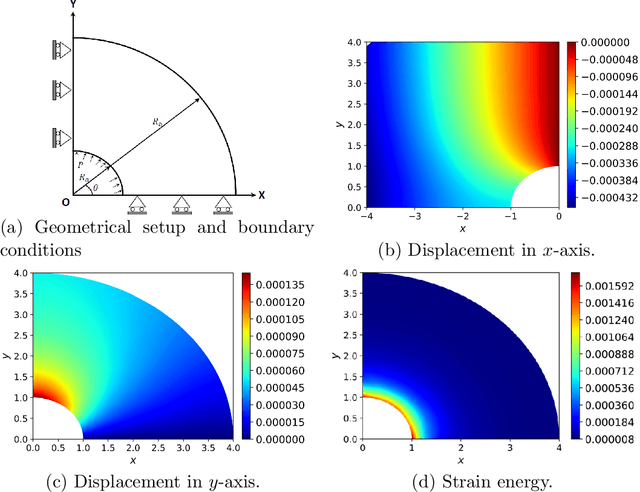
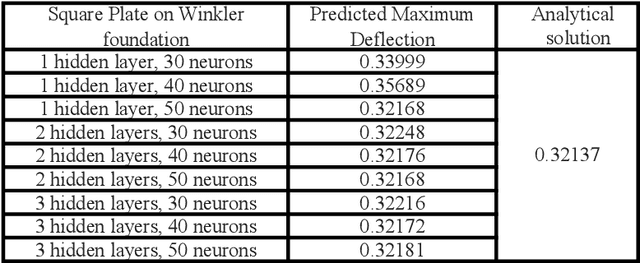
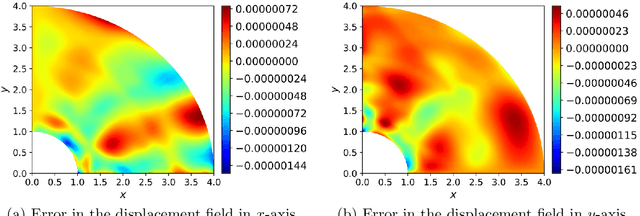
Partial Differential Equations (PDE) are fundamental to model different phenomena in science and engineering mathematically. Solving them is a crucial step towards a precise knowledge of the behaviour of natural and engineered systems. In general, in order to solve PDEs that represent real systems to an acceptable degree, analytical methods are usually not enough. One has to resort to discretization methods. For engineering problems, probably the best known option is the finite element method (FEM). However, powerful alternatives such as mesh-free methods and Isogeometric Analysis (IGA) are also available. The fundamental idea is to approximate the solution of the PDE by means of functions specifically built to have some desirable properties. In this contribution, we explore Deep Neural Networks (DNNs) as an option for approximation. They have shown impressive results in areas such as visual recognition. DNNs are regarded here as function approximation machines. There is great flexibility to define their structure and important advances in the architecture and the efficiency of the algorithms to implement them make DNNs a very interesting alternative to approximate the solution of a PDE. We concentrate in applications that have an interest for Computational Mechanics. Most contributions that have decided to explore this possibility have adopted a collocation strategy. In this contribution, we concentrate in mechanical problems and analyze the energetic format of the PDE. The energy of a mechanical system seems to be the natural loss function for a machine learning method to approach a mechanical problem. As proofs of concept, we deal with several problems and explore the capabilities of the method for applications in engineering.

Transfer learning enhanced physics informed neural network for phase-field modeling of fracture

We present a new physics informed neural network (PINN) algorithm for solving brittle fracture problems. While most of the PINN algorithms available in the literature minimize the residual of the governing partial differential equation, the proposed approach takes a different path by minimizing the variational energy of the system. Additionally, we modify the neural network output such that the boundary conditions associated with the problem are exactly satisfied. Compared to conventional residual based PINN, the proposed approach has two major advantages. First, the imposition of boundary conditions is relatively simpler and more robust. Second, the order of derivatives present in the functional form of the variational energy is of lower order than in the residual form. Hence, training the network is faster. To compute the total variational energy of the system, an efficient scheme that takes as input a geometry described by spline based CAD model and employs Gauss quadrature rules for numerical integration has been proposed. Moreover, we utilize the concept of transfer learning to obtain the crack path in an efficient manner. The proposed approach is used to solve four fracture mechanics problems. For all the examples, results obtained using the proposed approach match closely with the results available in the literature. For the first two examples, we compare the results obtained using the proposed approach with the conventional residual based neural network results. For both the problems, the proposed approach is found to yield better accuracy compared to conventional residual based PINN algorithms.