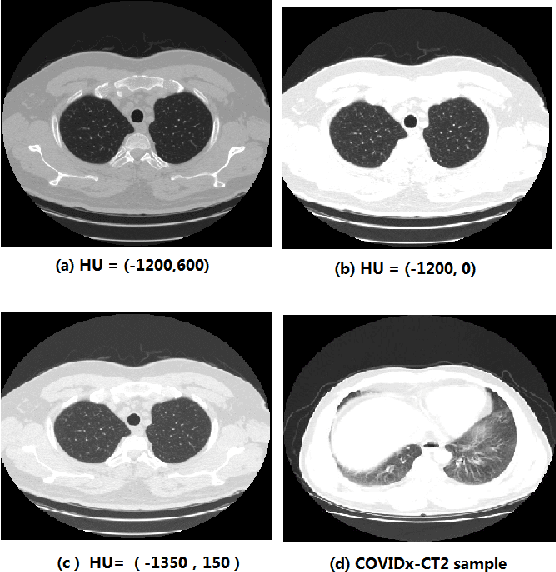
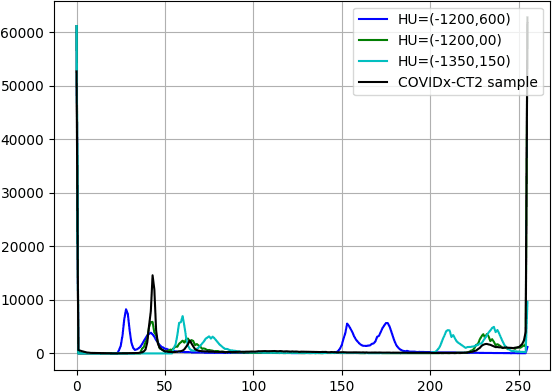
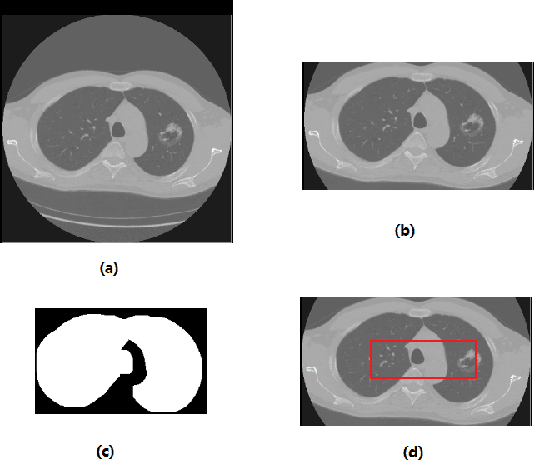
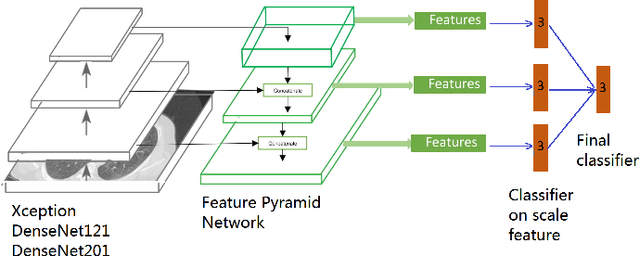
Data Augmentation and CNN Classification For Automatic COVID-19 Diagnosis From CT-Scan Images On Small Dataset

We present an automatic COVID1-19 diagnosis framework from lung CT images. The focus is on signal processing and classification on small datasets with efforts putting into exploring data preparation and augmentation to improve the generalization capability of the 2D CNN classification models. We propose a unique and effective data augmentation method using multiple Hounsfield Unit (HU) normalization windows. In addition, the original slice image is cropped to exclude background, and a filter is applied to filter out closed-lung images. For the classification network, we choose to use 2D Densenet and Xception with the feature pyramid network (FPN). To further improve the classification accuracy, an ensemble of multiple CNN models and HU windows is used. On the training/validation dataset, we achieve a patient classification accuracy of 93.39%.

A Fast Partial Video Copy Detection Using KNN and Global Feature Database

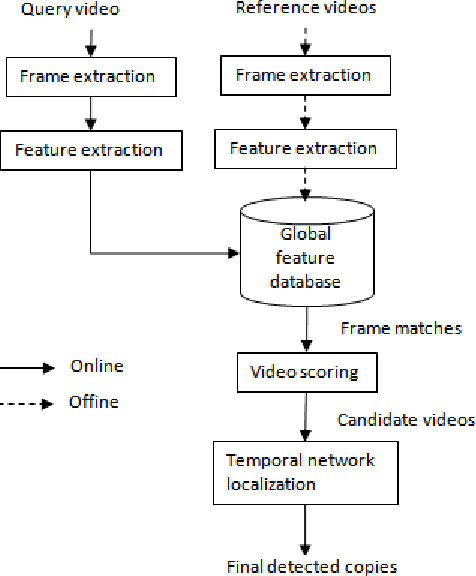
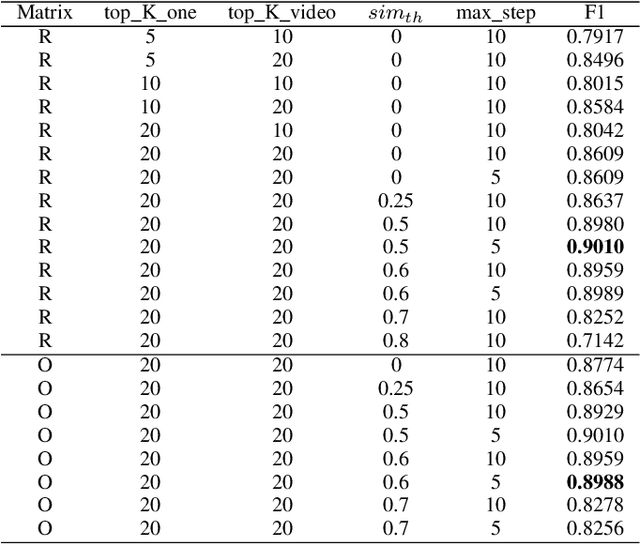
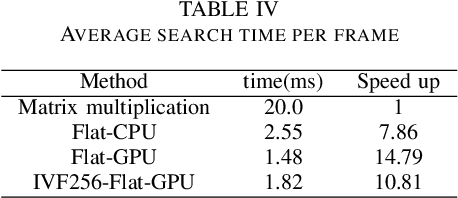
We propose a fast partial video copy detection framework in this paper. In this framework all frame features of the reference videos are organized in a KNN searchable database. Instead of scanning all reference videos, the query video segment does a fast KNN search in the global feature database. The returned results are used to generate a short list of candidate videos. A modified temporal network is then used to localize the copy segment in the candidate videos. We evaluate different choice of CNN features on the VCDB dataset. Our benchmark F1 score exceeds the state of the art by a big margin.

A Deep Collocation Method for the Bending Analysis of Kirchhoff Plate

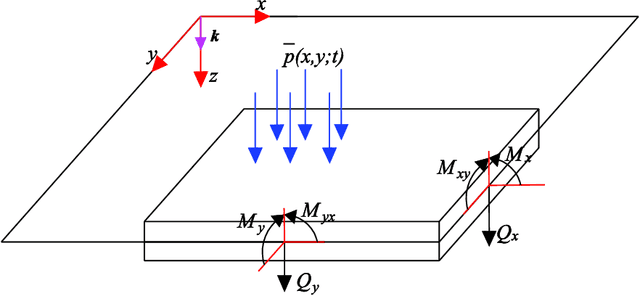
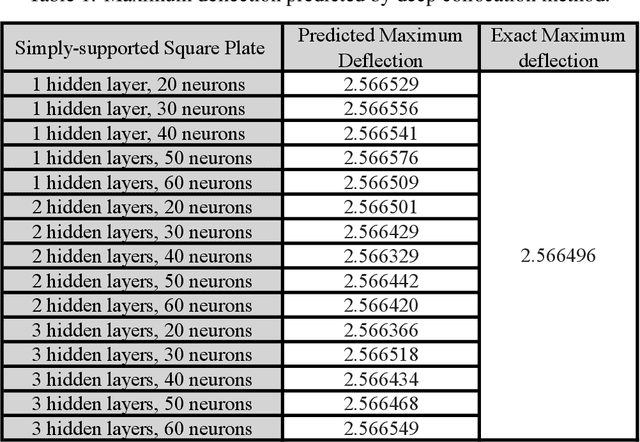
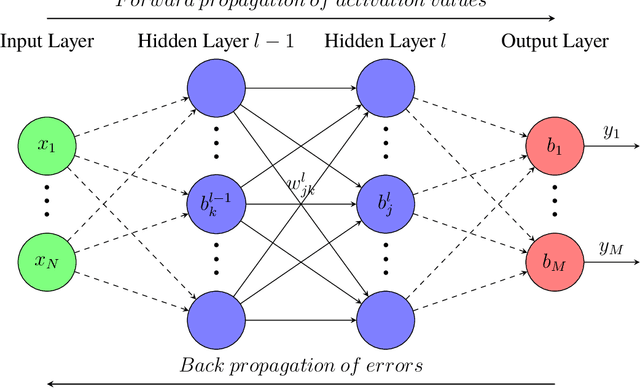
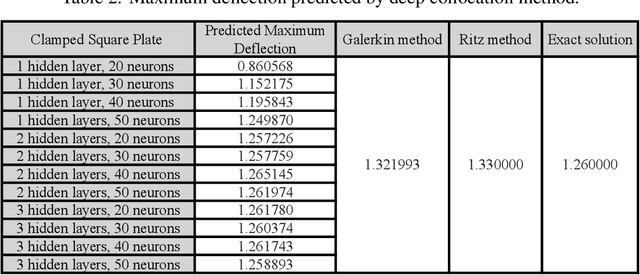
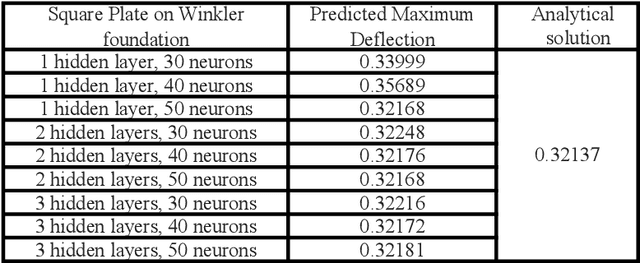
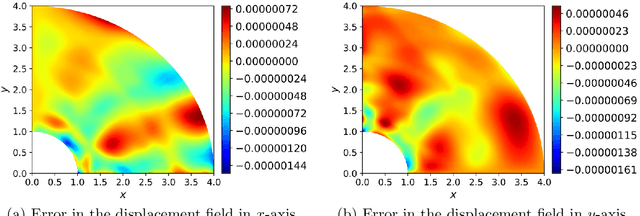
In this paper, a deep collocation method (DCM) for thin plate bending problems is proposed. This method takes advantage of computational graphs and backpropagation algorithms involved in deep learning. Besides, the proposed DCM is based on a feedforward deep neural network (DNN) and differs from most previous applications of deep learning for mechanical problems. First, batches of randomly distributed collocation points are initially generated inside the domain and along the boundaries. A loss function is built with the aim that the governing partial differential equations (PDEs) of Kirchhoff plate bending problems, and the boundary/initial conditions are minimised at those collocation points. A combination of optimizers is adopted in the backpropagation process to minimize the loss function so as to obtain the optimal hyperparameters. In Kirchhoff plate bending problems, the C1 continuity requirement poses significant difficulties in traditional mesh-based methods. This can be solved by the proposed DCM, which uses a deep neural network to approximate the continuous transversal deflection, and is proved to be suitable to the bending analysis of Kirchhoff plate of various geometries.

Deep Autoencoder based Energy Method for the Bending, Vibration, and Buckling Analysis of Kirchhoff Plates

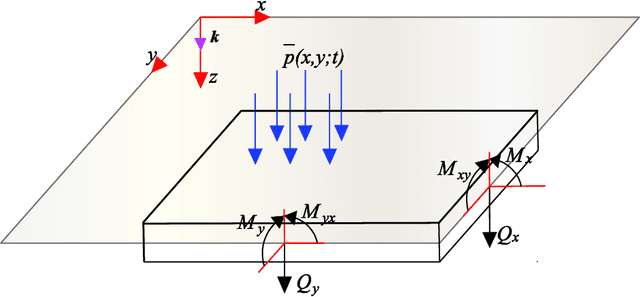
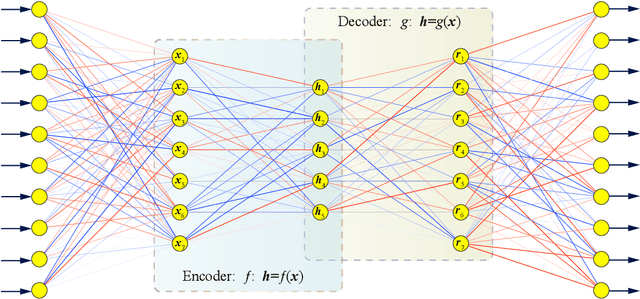
In this paper, we present a deep autoencoder based energy method (DAEM) for the bending, vibration and buckling analysis of Kirchhoff plates. The DAEM exploits the higher order continuity of the DAEM and integrates a deep autoencoder and the minimum total potential principle in one framework yielding an unsupervised feature learning method. The DAEM is a specific type of feedforward deep neural network (DNN) and can also serve as function approximator. With robust feature extraction capacity, the DAEM can more efficiently identify patterns behind the whole energy system, such as the field variables, natural frequency and critical buckling load factor studied in this paper. The objective function is to minimize the total potential energy. The DAEM performs unsupervised learning based on random generated points inside the physical domain so that the total potential energy is minimized at all points. For vibration and buckling analysis, the loss function is constructed based on Rayleigh's principle and the fundamental frequency and the critical buckling load is extracted. A scaled hyperbolic tangent activation function for the underlying mechanical model is presented which meets the continuity requirement and alleviates the gradient vanishing/explosive problems under bending analysis. The DAEM can be easily implemented and we employed the Pytorch library and the LBFGS optimizer. A comprehensive study of the DAEM configuration is performed for several numerical examples with various geometries, load conditions, and boundary conditions.

Analysis of three dimensional potential problems in non-homogeneous media with deep learning based collocation method

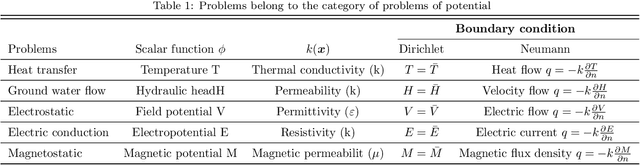
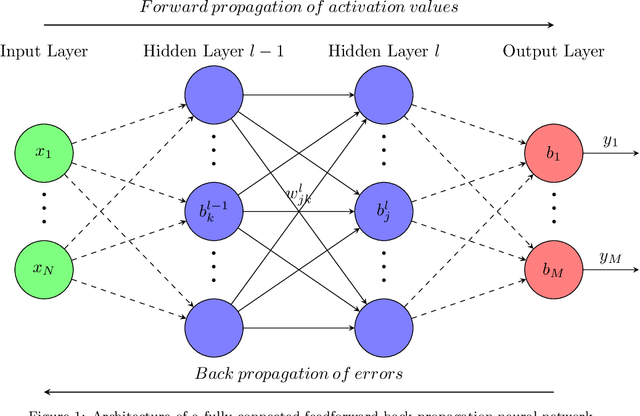
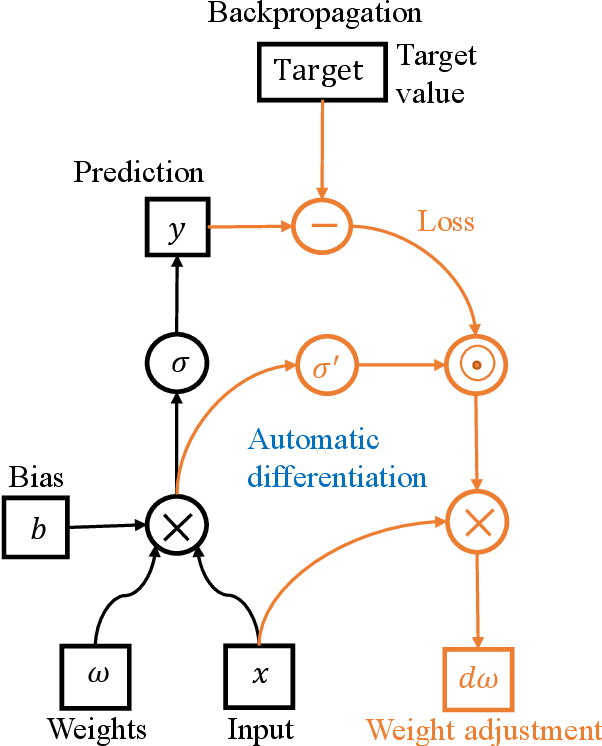
A deep learning based collocation method is presented in this paper to solve the three dimensional potential problems in non-homogeneous media. Based on the universal approximation theorem, the neural network can be utilized to approximate solutions for different PDEs in different geometries. The performance of deep learning based method depends on the configurations of the network and other hyper-parameter settings. This makes the choice of neural network configurations extremely important. The configuration of this deep collocation method is setup by comparing different schemes of smooth activation functions, sampling methods for collocation points generation, combined optimizers. Besides, a convergence proof of this deep collocation method in solving non-homogeneous potential problems is performed. Then the deep collocation method is applied to the analysis of different material variations, and it can be concluded that the deep collocation method predicts the temperature and flux accurately for different material variations, especially the exponential material variations. As a result, the deep learning based collocation method shows a great potential in approximating solutions to PDEs.

Stochastic groundwater flow analysis in heterogeneous aquifer with modified neural architecture search (NAS) based physics-informed neural networks using transfer learning

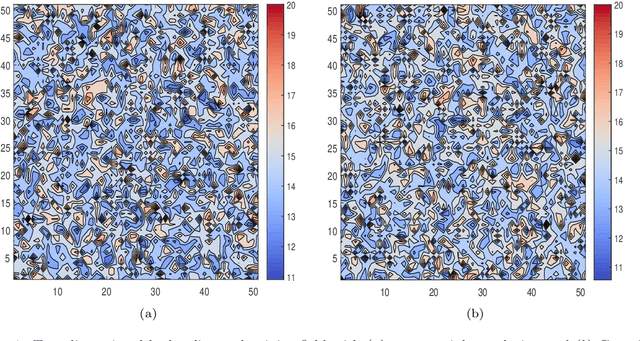
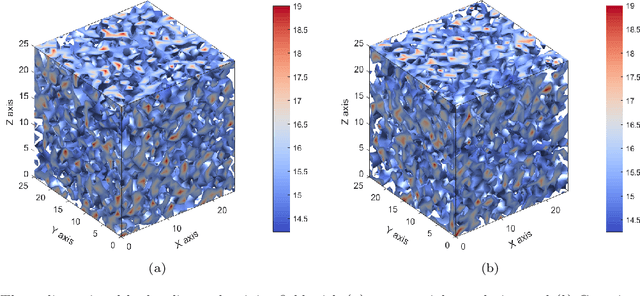
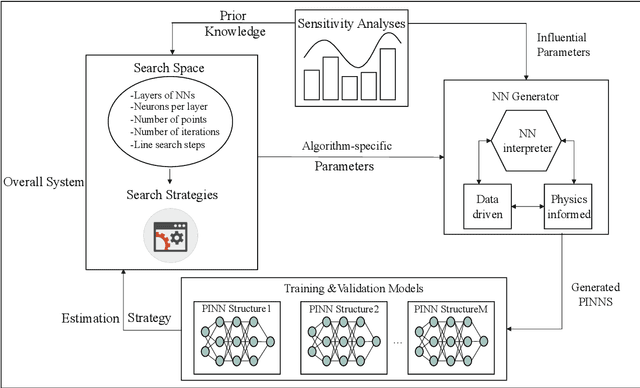
In this work, a modified neural architecture search method (NAS) based physics-informed deep learning model is presented to solve the groundwater flow problems in porous media. Monte Carlo method based on a randomized spectral representation is first employed to construct a stochastic model for simulation of flow through porous media. The desired hydraulic conductivity fields are assumed to be log-normally distributed with exponential and Gaussian correlations. To analyze the Darcy equation with the random hydraulic conductivity in this case when its intensity of fluctuations is small, the lowest-order perturbation theory is used to reduce the difficulty of calculations, by neglecting the higher-order nonlinear part. To solve the governing equations for groundwater flow problem, we build a modified NAS model based on physics-informed neural networks (PINNs) with transfer learning in this paper that will be able to fit different partial differential equations (PDEs) with less calculation. The performance estimation strategies adopted is constructed from an error estimation model using the method of manufactured solutions. Since the configuration selection of the neural network has a strong influence on the simulation results, we apply sensitivity analysis to obtain the prior knowledge of the PINNs model and narrow down the range of parameters for search space and use hyper-parameter optimization algorithms to further determine the values of the parameters. Further the NAS based PINNs model also saves the weights and biases of the most favorable architectures, which is then used in the fine-tuning process. The proposed NAS model based deep collocation method is verified to be effective and accurate through numerical examples in different dimensions using different manufactured solutions.

An Energy Approach to the Solution of Partial Differential Equations in Computational Mechanics via Machine Learning: Concepts, Implementation and Applications

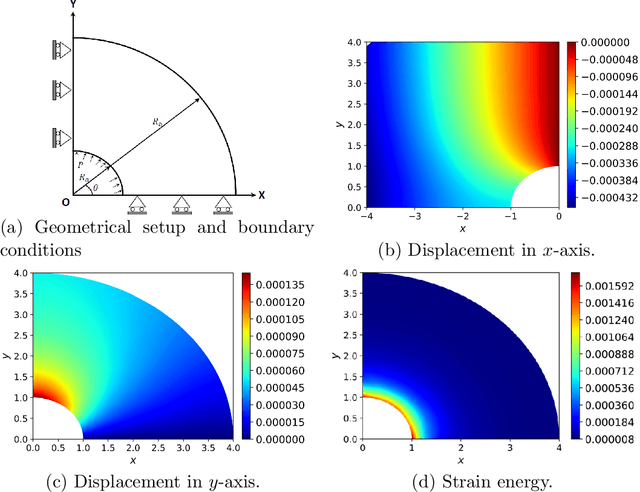
Partial Differential Equations (PDE) are fundamental to model different phenomena in science and engineering mathematically. Solving them is a crucial step towards a precise knowledge of the behaviour of natural and engineered systems. In general, in order to solve PDEs that represent real systems to an acceptable degree, analytical methods are usually not enough. One has to resort to discretization methods. For engineering problems, probably the best known option is the finite element method (FEM). However, powerful alternatives such as mesh-free methods and Isogeometric Analysis (IGA) are also available. The fundamental idea is to approximate the solution of the PDE by means of functions specifically built to have some desirable properties. In this contribution, we explore Deep Neural Networks (DNNs) as an option for approximation. They have shown impressive results in areas such as visual recognition. DNNs are regarded here as function approximation machines. There is great flexibility to define their structure and important advances in the architecture and the efficiency of the algorithms to implement them make DNNs a very interesting alternative to approximate the solution of a PDE. We concentrate in applications that have an interest for Computational Mechanics. Most contributions that have decided to explore this possibility have adopted a collocation strategy. In this contribution, we concentrate in mechanical problems and analyze the energetic format of the PDE. The energy of a mechanical system seems to be the natural loss function for a machine learning method to approach a mechanical problem. As proofs of concept, we deal with several problems and explore the capabilities of the method for applications in engineering.