Stochastic groundwater flow analysis in heterogeneous aquifer with modified neural architecture search (NAS) based physics-informed neural networks using transfer learning

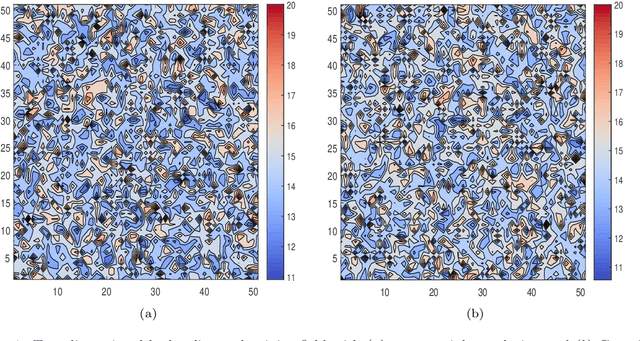
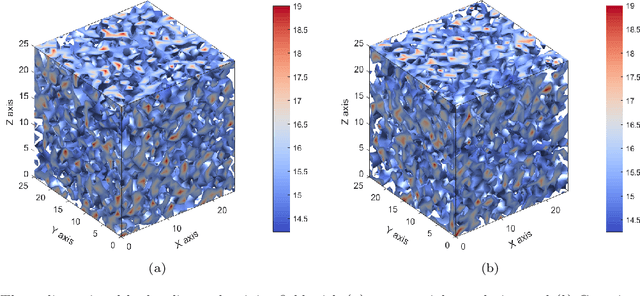
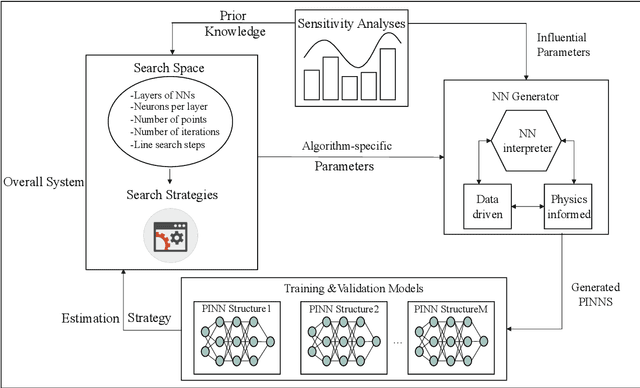
In this work, a modified neural architecture search method (NAS) based physics-informed deep learning model is presented to solve the groundwater flow problems in porous media. Monte Carlo method based on a randomized spectral representation is first employed to construct a stochastic model for simulation of flow through porous media. The desired hydraulic conductivity fields are assumed to be log-normally distributed with exponential and Gaussian correlations. To analyze the Darcy equation with the random hydraulic conductivity in this case when its intensity of fluctuations is small, the lowest-order perturbation theory is used to reduce the difficulty of calculations, by neglecting the higher-order nonlinear part. To solve the governing equations for groundwater flow problem, we build a modified NAS model based on physics-informed neural networks (PINNs) with transfer learning in this paper that will be able to fit different partial differential equations (PDEs) with less calculation. The performance estimation strategies adopted is constructed from an error estimation model using the method of manufactured solutions. Since the configuration selection of the neural network has a strong influence on the simulation results, we apply sensitivity analysis to obtain the prior knowledge of the PINNs model and narrow down the range of parameters for search space and use hyper-parameter optimization algorithms to further determine the values of the parameters. Further the NAS based PINNs model also saves the weights and biases of the most favorable architectures, which is then used in the fine-tuning process. The proposed NAS model based deep collocation method is verified to be effective and accurate through numerical examples in different dimensions using different manufactured solutions.